Relações Métricas de um Triângulo Retângulo são equações capazes de relacionar as medidas dos segmentos dentro de um triângulo retângulo. Leia nosso resumo e coloque seu conhecimento em prática com Exercícios de Relações Métricas no Triângulo Retângulo selecionados dos maiores vestibulares do Brasil.
Quando você terminar os Exercícios de Relações Métricas no Triângulo Retângulo, faça nosso Simulado Enem. Teste seu conhecimento, escolhendo as matérias que deseja praticar.
Uma das mais importantes formas geométricas para a matemática, é o triângulo. Ele é muito cobrado nos vestibulares e serve como base de compreensão de muitas outras figuras geométricas.
Chamamos de triângulo retângulo o triângulo que possui um dos três ângulos igual a 90°, também denominado de ângulo reto.
- Você sabe como Aprender Geometria?
O que são Relações Métricas no Triângulo Retângulo?
Relações Métricas de um Triângulo Retângulo são equações capazes de relacionar as medidas dos segmentos dentro de um triângulo retângulo. Saber essas equações fará com que você consiga fazer exercícios que envolvam triângulo de maneira mais rápida e precisa.
Para estudarmos as relações métricas, é necessário que você recorde algumas características do triângulo retângulo:
O triângulo retângulo possui um ângulo reto (90°). Dois dos seus lados são chamados Catetos e o terceiro é chamado de Hipotenusa.
Catetos
São os lados que formam o ângulo reto (90°), ou seja, são os lados que tocam neste ângulo.
Hipotenusa
É o lado que não toca no ângulo de 90°. É também o maior lado!

O que é o teorema de Pitágoras?
O Teorema de Pitágoras é a Primeira Relação Métrica do Triângulo Retângulo. Ele explica a relação entre os catetos e a hipotenusa. Representada com a seguinte fórmula:

Significa: a hipotenusa ao quadrado é igual ao cateto adjacente ao quadrado somado ao cateto oposto ao quadrado.
- Aprenda mais sobre Teorema de Pitágoras estudando Trigonometria.
Qual é a Segunda Relação Métrica do Triângulo Retângulo?
A hipotenusa é igual à soma das projeções dos catetos, observe:
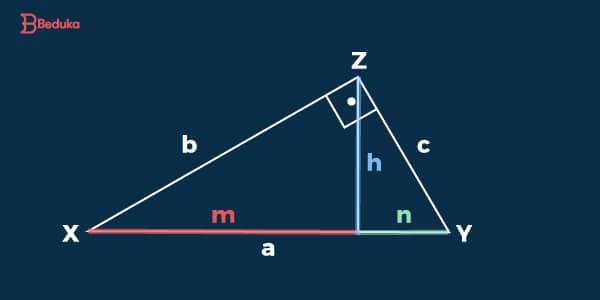
Chamamos de projeção dos catetos as partes representadas pela letra “m” e pela letra “n”. Sendo assim, podemos descrever a definição dada anteriormente de maneira muito simples:

Leia-se: a (hipotenusa) é igual ao valor de m (projeção do cateto) mais o valor de n (projeção do cateto).
Qual é a Terceira Relação Métrica do Triângulo Retângulo?
A altura ao quadrado é igual ao produto das projeções dos catetos.
Observe que a altura do triângulo está representada pela letra h, sendo assim, podemos descrever essa relação com a seguinte equação:
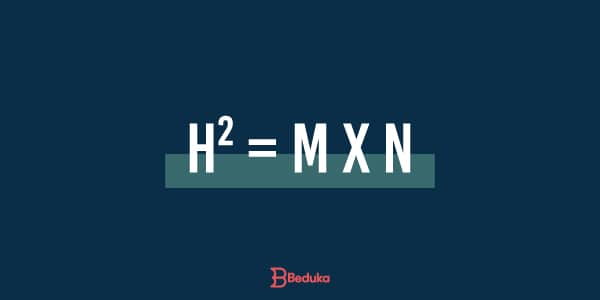
Leia-se: h (altura) ao quadrado é igual a m (projeção do cateto) vezes n (projeção do cateto).
Qual é a Quarta Relação Métrica do Triângulo Retângulo?
A quarta relação é utilizada para descobrir o valor dos catetos quando já sabemos o valor da projeção e o valor da hipotenusa.
Para ficar mais claro, observe as fórmulas, sempre baseando-se na seguinte imagem:
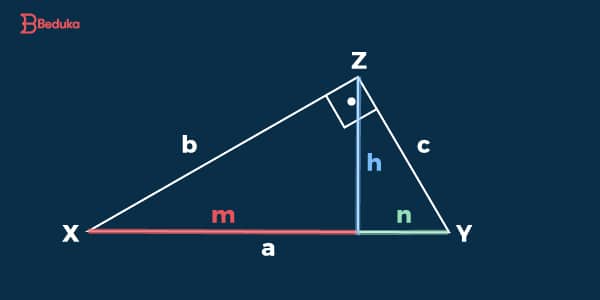
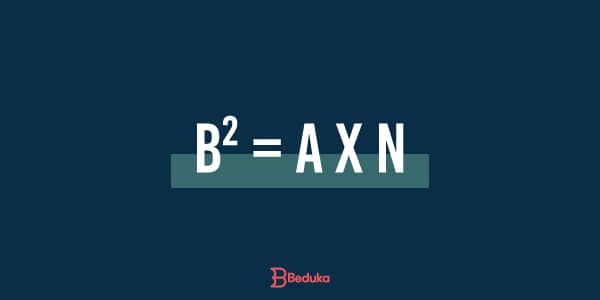
Leia-se: b² (cateto) ao quadrado é igual hipotenusa (a) multiplicada pela projeção do cateto (n)
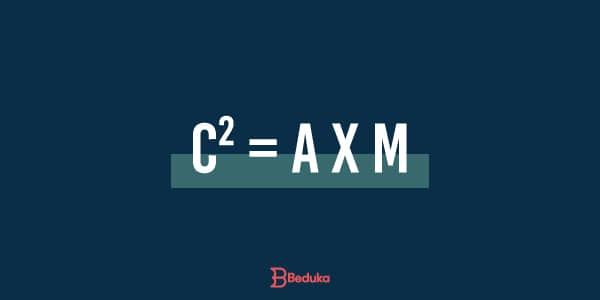
Leia-se: c² (cateto) ao quadrado é igual hipotenusa (a) multiplicada pela projeção do cateto (m)
Qual é a Quinta Relação Métrica do Triângulo Retângulo?
O produto entre a hipotenusa e a altura é sempre igual ao produto das medidas do catetos.
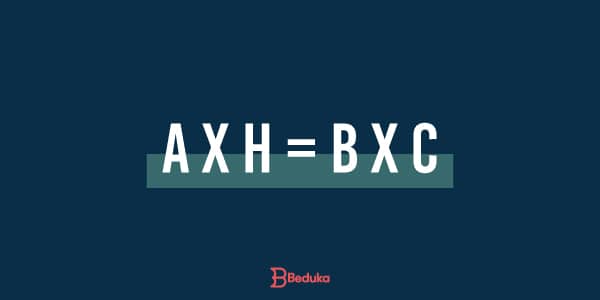
Leia-se = hipotenusa (a) vezes a altura é igual ao cateto (b) vezes o outro cateto [c].
- Aproveite para fazer mais Exercícios sobre Triângulos
Exercícios de Relações Métricas no Triângulo Retângulo
Chegou o momento de colocar em prática todo o seu conhecimento fazendo exercícios de Relações Métricas no Triângulo Retângulo.
Parabéns por ter lido até aqui!!!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Questão 1 – (IFSP/2015) O transporte alternativo é uma maneira de locomover-se usando um meio diferente dos mais tradicionais. A bicicleta é um exemplo disso. Em alguns lugares, ela é usada porque é mais barata, como no interior do Brasil e em países como a Índia e China. Outras pessoas escolhem andar de bicicleta por uma questão ideológica, porque elas não agridem o meio ambiente e não causam tantos transtornos quanto os carros. Usando uma bicicleta, uma pessoa sai do ponto A e dirige-se ao ponto B. O percurso, dado em km, representado pelos segmentos AC, CD e DB está esboçado no gráfico abaixo.
Considerando √2 = 1,4 assinale a alternativa que apresenta a distância percorrida pela pessoa do ponto A ao ponto B.
a) 56 km
b) 21 km
c) 20 km
d) 15 km
e) 10 km
Questão 2 – (IDECAN 2016) Um triângulo retângulo e possui uma hipotenusa que mede y e um de seus catetos vale x. Um ângulo a é marcado neste triângulo, conforme mostra figura:
Sabendo que , pode-se concluir que o ângulo a vale:
a) 15°
b) 30°
c) 45°
d) 60°
Questão 3 – (UNESP 2017) Arthur desenhou numa folha de papel o triângulo retângulo a seguir. Ele afirmou, corretamente, que a medida do segmento XY a medida do segmento YZ é igual à medida do segmento XZ mais ________ cm.
Das alternativas a seguir, aquela que completa corretamente a afirmação de Arthur é:
a) 6
b) 5
c) 4
d) 3
e) 2
Questão 4 – (IBADE 2018) Considere um triângulo retângulo tal que o cosseno de um de seus ângulos agudos é igual a 0,8. Sabendo-se que a hipotenusa desse retângulo é igual a 4, o valor da tangente deste mesmo ângulo é:
a) 0,75
b) 1
c) 0,7
d) 0,5
Questão 5 – (UFRR 2015) Sobre os lados do triângulo retângulo ABC, foram desenhados pentágonos regulares cujas áreas são S1 ,S2 e S3 , conforme indica a figura abaixo. Sabendo-se que 2 3 os lados AB e AC têm o mesmo comprimento, é correto afirmar que:
a) S1 < S2 < S3
b) S1² = S2² + S3³
c) S1 > S2 + S3
d) S1 = S2 + S3
e) S2 = S1 / S3
Respostas dos exercícios de Exercícios de Relações Métricas no Triângulo Retângulo
Exercício resolvido da questão 1 –
Alternativa correta: a) 56 km
Exercício resolvido da questão 2 –
Alternativa correta: b) 30°
Exercício resolvido da questão 3 –
Alternativa correta: a) 6
Exercício resolvido da questão 4 –
Alternativa correta: a) 0,75
Exercício resolvido da questão 5 –
Alternativa correta: d) S1 = S2 + S3
Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos Exercícios de Relações Métricas no Triângulo Retângulo? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.





