São denominas de Inequações do 2° grau as relações de desigualdade que são compostas por expressões matemáticas de grau 2. Este post vai te ensinar de maneira simples como dominar as operações com inequações. Leia nosso resumo e faça nossa lista de Exercícios de Inequações do 2° grau.
Quando você terminar os Exercícios de Inequações do 2° grau, faça nosso Simulado Enem. Coloque em prática todo o seu estudo, escolhendo as matérias que deseja treinar.
A palavra inequação costuma criar um bloqueio nos estudantes que imaginam nela um verdadeiro bicho de sete cabeças.
Nesse post, nós iremos simplificar para que você chegue no ENEM dominando operações com Inequações do 2° grau.
Para isso, é muito importante que você leia até o final e faça nossa lista de exercícios selecionada dos maiores vestibulares do Brasil!
- É possível aprender Inequação de 1° Grau de forma simples, acredite!
O que é Inequação do 2° grau?
São denominadas de Inequações do 2° grau as relações de desigualdade que são compostas por expressões matemáticas de grau 2. Essa comparação pode ser dada da seguinte forma:
- ax² + bx + c > 0, ou seja, a operação (ax² + bx + c) dá um resultado maior (>) do que zero;
- ax² + bx + c ≥ 0, ou seja, a operação (ax² + bx + c) dá um resultado maior (>) ou igual (=) a zero;
- ax² + bx + c < 0, ou seja, a operação (ax² + bx + c) dá um resultado menor (<) do que zero;
- ax² + bx + c ≤ 0, ou seja, a operação (ax² + bx + c) dá um resultado menor (<) ou igual (=) a zero;

Qual a diferença entre Equação do 2° grau e Inequação do 2° grau?
As equações do 2° grau são relações de igualdade e sua resolução se dá pelos únicos valores que X pode adotar para que a sentença seja verdadeira.
Já as Inequações do 2° grau são as relações de desigualdade e sua resolução se dá pela busca de alguns valores de X capazes de satisfazer a equação.
Esses valores, agrupados, são denominados de conjunto solução.
- É muito importante saber O que São Equações Exponenciais.
Como resolver uma Inequação de 2° grau?
Para resolver Inequações do 2° grau precisamos transformar as expressões em funções. Feito isso, basta estudar quais valores de X fazem com que o sinal da função seja obedecido.

- É muito necessário prestar bastante atenção no sinal de desigualdade e lembrar que a forma como resolvemos Inequações do 1° grau é DIFERENTE da forma com a qual resolvemos Inequações do 2° grau.
Sabia que é possível resolver uma inequação do 2° grau em 9 passos?
Acreditando que praticar é essencial, antes de partirmos para uma lista com exercícios selecionados para você, vamos dar um exemplo de como resolver um problema envolvendo Inequação do 2° grau em apenas 9 passos.
Exemplo
X² – 4X -5 < 0
Passo 1 – Devemos inicialmente buscar uma série de valores de X que permitem que X² – 4x -5 seja um valor menor do que zero.
Passo 2 – Logo, devemos transformar essa expressão em uma função f(x);
Passo 3 – A partir daí, estudaremos os sinais no objetivo de determinar valores de x onde a função é negativa, ou seja, menor do que zero.
Vamos lá?
Passo 4 – f(x) = X² -4X – 5
Lembrando dos termos das equações, tenho que:
a = 1
b = -4
c= – 5
Como sei disso?
Lembre-se de uma expressão genérica do segundo grau: aX² + bX + c = 0. Apenas identifiquei os coeficientes a,b e c.
Passo 5 – Sabendo que o coeficiente a é positivo, também sei que quando eu representar esta inequação graficamente, terei uma parábola côncava para cima, sorridente.
Vamos continuar para calcular a discriminante:
Passo 6 –

Passo 7 – Sendo essa discriminante maior do que 0, sabemos que ela possui duas raízes reais e distintas. Utilizaremos a Fórmula de Bháskara para descobrir essas raízes:
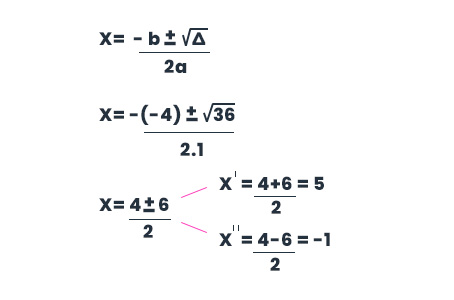
- A Fórmula de Bháskara é essencial para aprender matemática
Passo 8 – Precisamos encontrar o conjunto de valores de X para que a Inequação do 2° grau obedeça aquilo que ela diz, ou seja, tenha um valor menor do que zero.
Esse valor não pode ser 4 e nem -2, pois isso zeraria a equação e queremos que ela seja algum número menor que 0.
Por isso sabemos que os valores possíveis para X estão entre -2 e 4, sem incluir -2 e 4, daí o fato da bolinha estar aberta na representação gráfica.
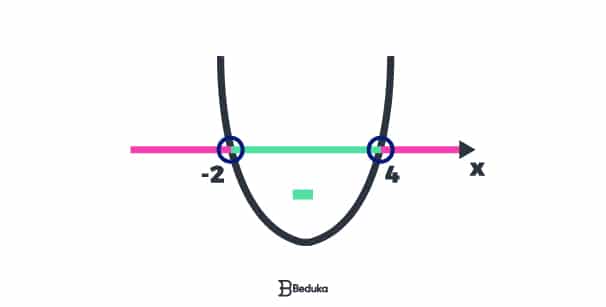
Passo 9 – Assim, podemos concluir que qualquer valor real entre -2 e 4 satisfaria a nossa Inequação do 2° grau, sendo assim, esse é o nosso conjunto solução:
S = {x ∈ ℝ | –2 < x < 4 }
Agora que você aprendeu esse hack das Inequações, coloque seu conhecimento em prática com Exercícios de Inequações do 2° grau.
Exercícios de Inequações do 2° grau
Chegou o momento de colocar na prática todo o seu conhecimento fazendo exercícios de Inequações do 2° grau.
Parabéns por ter lido até aqui!!!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Questão 1 – (PUC-RIO 2009) Quantas soluções inteiras a inequação x² + x – 20 ≤ 0 admite?
a) 2
b) 3
c) 7
d) 10
e) 13
Questão 2 – (UDESC 2008) O conjunto solução da inequação x² – 2x – 3 ≤ 0 é:
a) {x R/ -1 < x < 3}
b) {x R/ -1 < x ≤ 3}
c) {x R/x < -1 ou x > 3}
d) {x R / -1 ≤ -1 ou ≥ 3}
e) {x R/ -1 ≤ x ≤ 3}
Questão 3 – (UFRGS 2017) Sendo a e b números reais, considere as afirmações a seguir.
I) Se a < b então –a > –b .
II) Se a > b então 1/a < 1/b .
III) Se a < b então a2 < b2 .
Quais estão corretas?
a) Apenas I
b) Apenas II
c) Apenas III
d) Apenas I e II
e) I,II e II.
Questão 4 – (BNDES – Cesgranrio). O conjunto-solução da inequação 9 – x² > 0 é:
a) – 3 > x > 3
b) – 3 < x < 3
c) x = 3
d) x < 3
e) x > 3
Questão 5 – (BB – Cesgranrio). A proposição funcional “Para todo e qualquer valor de n, tem-se 6n < n² + 8 ” será verdadeira, se n for um número real
a) menor que 8.
b) menor que 4.
c) menor que 2.
d) maior que 2.
e) maior que 3.
Questão 6 – (RFB – Esaf) Considere as inequações dadas por:
f(x) = x² – 2x + 1 ≤ 0
g(x) = -2x² + 3x + 2 ≥ 0
Sabendo-se que A é o conjunto solução de f(x) e B o conjunto solução de g(x), então o conjunto Y = A ∩ B é igual a:
a) Y = { x ∈ R | -1/2 < x ≤ 2 }
b) Y = { x ∈ R | -1/2 ≤ x ≤ 2 }
c) Y = { x ∈ R | x = 1 }
d) Y = { x ∈ R | x ≥ 0 }
e) Y = { x ∈ R | x ≤ 0 }
Respostas dos exercícios de Inequações do 2° grau:
Exercício resolvido da questão 1 –
Alternativa correta: d) 10
Exercício resolvido da questão 2 –
Alternativa correta: e) {x R/ -1 ≤ x ≤ 3}
Exercício resolvido da questão 3 –
Alternativa correta: a) Apenas I
Exercício resolvido da questão 4 –
Alternativa correta: b) – 3 < x < 3
Exercício resolvido da questão 5 –
Alternativa correta: c) menor que 2.
Exercício resolvido da questão 6 –
Alternativa correta: c) Y = { x ∈ R | x = 1 }
Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos Exercícios de Inequações do 2° Grau? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.






6 Comentários
Olá, a resposta da questão 2 está errada, a alternativa correta é a letra E
Muito Obrigado pela informação, Luís Gustavo! Corrigimos!
O valor de b substituído para encontrar as raízes,x’ e x” de ser 4, e não 2. No exercício de exemplo: x² – 4x + 5 = 0.
Oi, Marcelo! O valor utilizado foi 4 mesmo.
Oi, na explicação, no passo 7 a raiz que foi usada foi uma raiz de 96, quando o delta resultante foi de 36, e também o -(-4) se tornou um 2. Em tese as raízes são 5 e -1 da primeira inequação de exemplo mas tirando isso está ótimo
Oi, Mateus! Agradecemos o aviso e já fizemos a correção.