Geometria espacial é a área da Matemática responsável pela investigação de sólidos no espaço, ou seja, ela analisa objetos tridimensionais. Essas formas são compostas por pontos, retas e planos. Leia nosso resumo e coloque em prática todo o seu conhecimento com Exercícios de Geometria Espacial.
Quando você terminar os Exercícios de Geometria Espacial, faça nosso Simulado Enem. Coloque em prática todo o seu estudo, escolhendo as matérias que deseja treinar.
Observe a diferença entre as duas imagens:

- Perceba que a primeira casa não possui profundidade, é o que chamamos de 2D (duas dimensões);
- Já a segunda casa possui três dimensões, é o que chamamos de 3D (3 dimensões).
Um objeto geométrico espacial, é como a casa em 3D, eles possuem profundidade. Logo, as suas medidas levam em conta as três dimensões do objeto.
Neste post nós iremos estudar quais as características de um objeto espacial e como analisá-los no vestibular.
Para isso, ao final, selecionamos Exercícios de Geometria Espacial dos melhores Vestibulares do Brasil.
O que é Geometria Espacial?
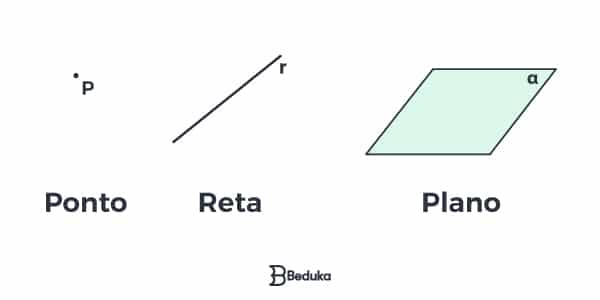
Geometria espacial é a área da Matemática responsável pela investigação de sólidos no espaço, ou seja, ela analisa objetos tridimensionais. Essas formas são compostas por pontos, retas e planos.
Quais as Classificações dos Sólidos Espaciais?
Os Sólidos Espaciais podem ser classificados em três tipos:
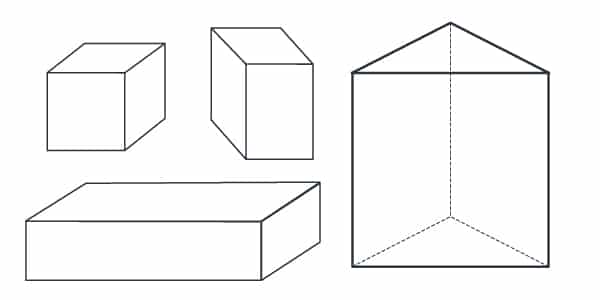
Poliedros: são fechados e constituídos de vértice, aresta e face.
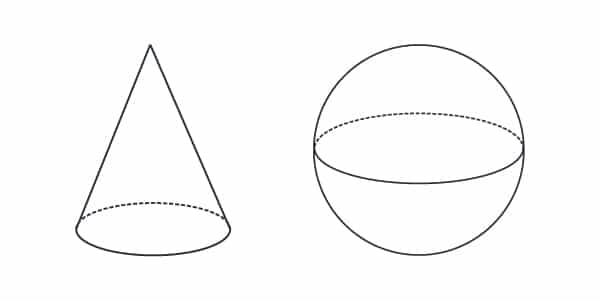
Corpos redondos: são aqueles que apresentam curvas e a sua medida específica é o raio (r).
Sólidos de Platão: Os 5 sólidos teorizados por Platão são: tetraedro (pirâmide), hexaedro (cubo), octaedro (8 faces), dodecaedro (12 faces) e icosaedro (20 lados).
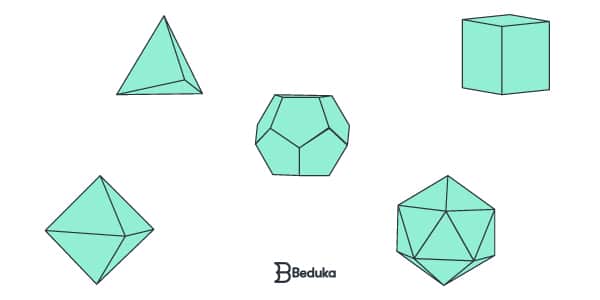
Esses poliedros são classificados assim, pois possuem arestas e faces congruentes. Também são chamados de poliedros regulares. Platão os analisou para tentar entender o surgimento do mundo através das formas geométricas.
Fórmulas da Geometria Espacial
Na Geometria Espacial o objetivo do cálculo é descobrir o espaço ocupado (volume) e os contornos (área total), mas respeitando as dimensões a mais que os sólidos têm.
Cubo: volume e área total
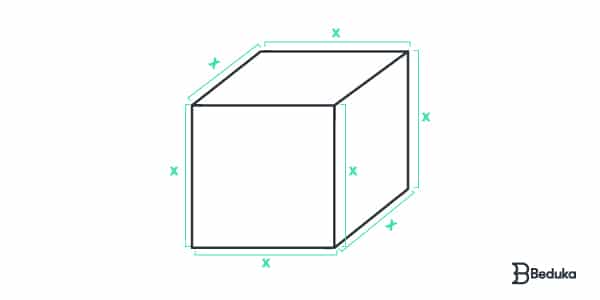
O volume é dado multiplicando os valores das três dimensões. Como o cubo é formado por arestas de medidas iguais, podemos calcular seu volume simplesmente como:
- V = (aresta)³
Da mesma forma, o cubo possui 6 faces de áreas iguais, portanto, a sua área total pode ser dada simplesmente por:
- At = 6 . (aresta)²
Paralelepípedo volume e área total
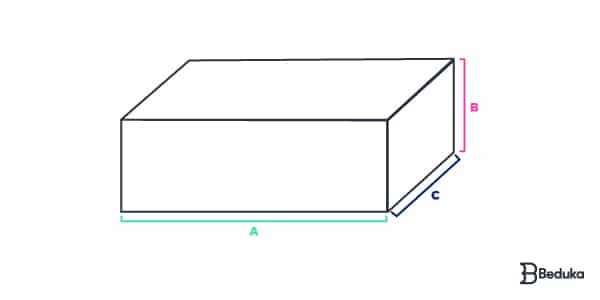
Se um paralelepípedo possui dimensões a, b, c; então:
- V = a . b . c
- At = 2ab + 2ac + 2bc
Prisma e Pirâmide: volume e área total
O volume e a área total do prisma e da pirâmide dependem do polígono que está na base, por isso usamos Ab: área da base (pode ser um triângulo, quadrado, hexágono, etc.) e Al: área lateral (retângulos para prismas e triângulos para pirâmides).
O volume deles dependem diretamente da área da base e da altura (h)!
Exemplo: Prisma de base triangular (pbt)
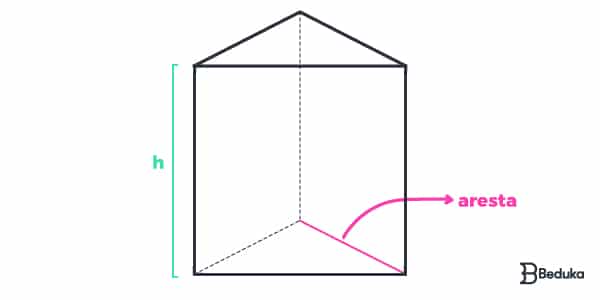
- V (pbt) = Ab . h
- At (pbt) = 2Ab + Al
(se as 2 bases são um triângulo, logo, ab será a área dos 2 triângulos!)
Exemplo: Pirâmide de base quadrada (pbq)
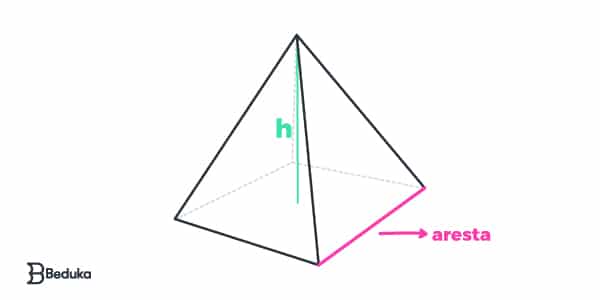
- V (pbt) = ⅓ Ab . h
(diferente dos primas, a pirâmide sofre um afunilamento no volume, por isso, contabilizamos apenas ⅓ da área da base).
- At (pbt) = Ab + Al
(se a base é um quadrado, ab será a fórmula da área do quadrado)
Cilindro: volume e área total
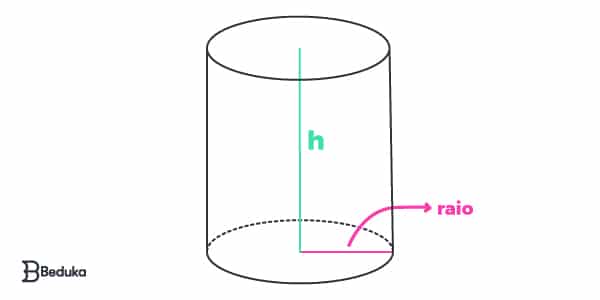
As medidas de corpos redondos são dadas pelo raio (r) e altura (h). Portanto:
- V = π .r . 2 . h
- At = 2. π. r . (r + h)
Cone: volume e área total
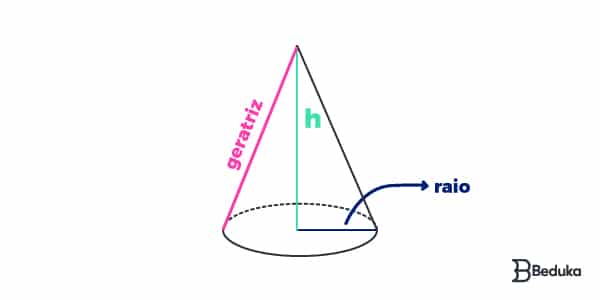
Para calcular a medida da área do cone, primeiro precisamos descobrir a geratriz (g), segmentos que iniciam na extremidade do vértice, percorre a superfície do cone e termina em um vértice da circunferência.
Para calcular a geratriz em um cone reto, basta utilizar trigonometria ou o teorema de pitágoras!
- At = π. r . (g + r)
- V = ⅓ . π . r . 2 . h
Esfera: volume e área total
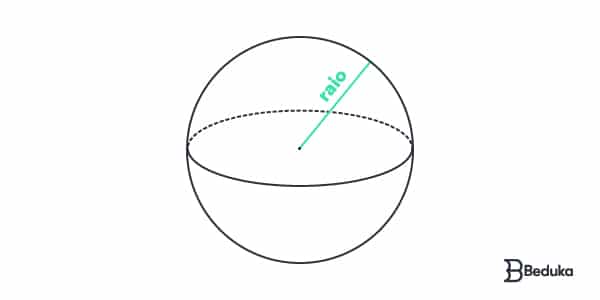
Esse é o mais diferente de todos pois não possui faces com planos definidos!
- At = 4 . π . r²
- V = 4 ⁄ 3. π . r³
O que é a Relação de Euler?
O matemático Euler percebeu uma relação entre o número de vértices (V), arestas (A) e faces (F), conhecida como relação de Euler, dada pela expressão:
V – A + F = 2
Leia-se: vértices menos arestas mais faces é igual a dois
Logo, com base na equação, descobre-se a quantidade de arestas que um sólido possui pelo número de faces e de vértices.
- Aproveite a oportunidade para aprender Geometria Plana!
Exercícios de Geometria Espacial com Gabarito
No início, essa matéria até assusta, mas agora sei que com esse resumo tudo ficou mais claro para você. Que tal testar seu conhecimento com Exercícios de Função Exponencial.
Parabéns por ter lido até aqui!!!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Questão 1 – (Enem) Para resolver o problema de abastecimento de água, foi decidida, numa reunião do condomínio, a construção de uma nova cisterna. A cisterna atual tem formato cilíndrico, com 3 m de altura e 2 m de diâmetro, e estimou-se que a nova cisterna deverá comportar 81 m³ de água, mantendo o formato cilíndrico e a altura da atual. Após a inauguração da nova cisterna, a antiga será desativada. (Utilize 3,0 como aproximação para π.)
Qual deve ser o aumento, em metros, no raio da cisterna para atingir o volume desejado?
a) 0,5
b) 1,0
c) 2,0
d) 3,5
e) 8,0
Questão 2 – (IFG) As medidas internas de um reservatório no formato de um paralelepípedo são de 2,5 m de comprimento, 1,8 m de largura e 1,2 m de profundidade (altura). Se, em um determinado momento do dia, esse reservatório está apenas com 70% de sua capacidade, a quantidade de litros que faltam para enchê-lo é igual a:
a) 1620
b) 1630
c) 1640
d) 1650
e) 1660
Questão 3 – (Enem 2010) A siderúrgica “Metal Nobre” produz diversos objetos maciços utilizando o ferro. Um tipo especial de peça feita nessa companhia tem o formato de um paralelepípedo retangular, de acordo com as dimensões indicadas na figura que segue.
O produto das três dimensões indicadas na peça resultaria na medida da grandeza:
a) massa
b) volume
c) superfície
d) capacidade
e) comprimento
Questão 4 – (UFRGS 2017) Considere a planificação de um tetraedro, conforme a figura abaixo.
Os triângulos ABC e ABD são isósceles respectivamente em B e D. As medidas dos segmentos AC , BC , BD e DF estão indicadas na figura.
A soma das medidas de todas as arestas do tetraedro é:
a) 33
b) 34
c) 43
d) 47
e) 48
Questão 5 – (Fuvest-SP) Uma superfície esférica de raio 13 cm é cortada por um plano situado a uma distância de 12 cm do centro da superfície esférica, determinando uma circunferência. O raio dessa circunferência, em centímetros, é
a) 5
b) 4
c) 3
d) 2
Gabarito dos Exercícios de Geometria Espacial
Exercício resolvido da questão 1 –
Alternativa correta: c) 2,0
Exercício resolvido da questão 2 –
Alternativa correta: a) 1620
Exercício resolvido da questão 3 –
Alternativa correta: b) volume
Exercício resolvido da questão 4 –
Alternativa correta: a) 33
Exercício resolvido da questão 5 –
Alternativa correta: a) 5
Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos Exercícios de Geometria Espacial? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.






9 Comentários
Primeira questão a resposta não seria a (D) ?
E a letra C mesmo, Teodorico.
V = π .r . 2 . h
aki n seria na vdd V=π.r².h?
π.r² sendo a área da base, ou seja a área do circulo?
É isso mesmo, Thiago. Aconteceu de o 2 não ficar em forma de potência.
Depois de resolvida a questão, o raio será raiz quadrada de 9 que é igual a 3, portanto 3 – 2=1, significa que o raio será aumentado em 1m, considerando que o raio anterior era de 2m. Resposta correta, letra b.
O volume de um cilindro é dado pela fórmula π.r².H. A cisterna deverá ter de 81 m³, portanto temos que π.r².3 = 81. Assim, encontramos π = 3 e 9r² = 81. Fazendo essa conta, achamos raio igual a 3, logo foram 2 metros a mais de raio. Nosso gabarito está certo.
Mas, na questão 1, a capacidade será de apenas 36m³… a resposta é realmente a letra C? então, eu não entendi.
Oh, espere! Já entendi… Meu erro foi de interpretação de texto mesmo. É a letra C.
Oh, espere! O meu erro foi a falta de interpretação mesmo. Letra C, a correta.