Exercícios de Escala com Gabarito

A razão constante que permite uma comparação entre qualquer grandeza, é chamada de escala. Ela é um mecanismo utilizado para representar algo de maneira proporcional, como, por exemplo, representar um território em um mapa. Leia nosso resumo e coloque seu conhecimento em prática com nossa lista de Exercícios de Escala selecionados dos maiores vestibulares do Brasil.

Quando você terminar os Exercícios de Escala, faça nosso Simulado Enem. Coloque em prática todo o seu estudo, escolhendo as matérias que deseja praticar.

Quando você abre um mapa físico ou o Google Maps, os tamanhos dos territórios não são escolhidos aleatoriamente. 

Eles possuem uma escala, ou seja, cada cm do mapa corresponde a um tamanho maior no espaço real.

• A Terra e seus espaços são representados pelas Projeções Cartográficas.

O que é Escala?

É chamada de escala a razão constante que permite uma comparação entre qualquer grandeza. Ela é um mecanismo utilizado para representar algo de maneira proporcional, como, por exemplo, representar um território em um mapa.

A escala utilizada para representar mapas é denominada de Escala Cartográfica.

Como representar uma escala?

A forma de representar uma escala é a seguinte:

• Escala = tamanho na imagem / tamanho no objeto real

Também pode ser representado por:

• Escala = medida na imagem : medida no objeto real

Vamos pensar em um mapa que tem a escala 1:70, isso nos mostra que a cada 1cm de desenho no mapa, equivale a 70 cm no objeto real.

Logo, a partir dessa escala, se uma casa tivesse 8 cm de comprimento em uma parede, ela teria 560 cm, ou 5,6m, de comprimento na realidade.

Lembrando que eu posso informar a minha escala já convertendo as unidades de medida, por exemplo, informando ao leitor do mapa que 1 cm no mapa equivale a 0,7m na vida real.

Tudo o que importa quando falamos sobre escala, é manter a proporção adequada e constante. 

Caso aumente no mapa, aumenta proporcionalmente a área da vida real que está sendo representada.

Depois de entender a teoria por trás da escala matemática, você perceberá que calculá-la é muito simples.

Como calcular uma escala?

A escala matemática ou cartográfica é calculada pela seguinte equação:

Exemplo:

Um mapa possui uma escala de 1:400000, ou seja, a cada 1 cm de mapa, eu tenho 400.000 cm de território real. 

Supondo que o pedaço que nós desejamos descobrir o tamanho no mapa, tem 8 centímetros.

Devemos aplicar a fórmula para descobrir quanto de tamanho real, 8 centímetros de mapa representa:

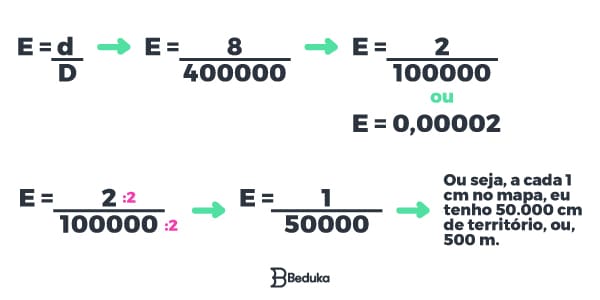
Dica: é possível acelerar o processo, simplificando 8/400000 por 8, da seguinte forma: 

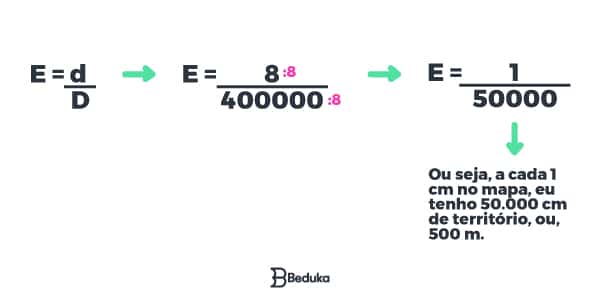
• Para aprender escala, é necessário saber o que é fração!

Quais os tipos de escalas?

• Escala ampliada: Quando o tamanho da representação é maior do que o objeto real. Muito utilizada para representar objetos muito pequenos (células, ossos, anatomias vegetais, etc…) ou detalhes de lugares (quinas de uma casa ou peças eletrônicas, por exemplo).

• Escala reduzida: quando o tamanho real é maior do que a representação. Por exemplo, o mapa mundi ou o Google Maps citados anteriormente.

• Escala natural: quando a representação é exatamente igual ao objeto real. Por exemplo, a escala da confecção de bonecos de cera de  famosos que existem em vários lugares do mundo.

Depois de fazer os Exercícios de Escala, que tal afiar seu conhecimento com Exercícios de Fração? 

Exercícios de Escala com Gabarito

Chegou o momento de colocar na prática todo o seu conhecimento fazendo exercícios de Escala. 

Parabéns por ter lido até aqui!!! 

Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.

Questão 1 – (ENEM) Sabe-se que a distância real, em linha reta, de uma cidade A, localizada no estado de São Paulo, a uma cidade B, localizada no estado de Alagoas, é igual a 2 000 km. Um estudante, ao analisar um mapa, verificou com sua régua que a distância entre essas duas cidades, A e B, era 8 cm.

Os dados nos indicam que o mapa observado pelo estudante está na escala de

a) 1 : 250.

b) 1 : 2 500.

c) 1 : 25 000.

d) 1 : 250 000.

e) 1 : 25 000 000.

Questão 2 – (Mackenzie) Considerando que a distância real entre Yokohama e Fukushima, duas importantes localidades, onde serão realizadas competições dos Jogos Olímpicos de Verão 2020 é de 270 quilômetros, em um mapa, na escala de 1:1.500.000, essa distância seria de

a) 1,8 cm

b) 40,5 cm

c) 1,8 m

d) 18 cm

e) 4,05 m

Questão 3 – (UFPB) Escala gráfica, segundo Vesentini e Vlach (1996, p. 50), “é aquela que expressa diretamente os valores da realidade mapeada num gráfico situado na parte inferior de um mapa”. Nesse sentido, considerando que a escala de um mapa está representada como 1:25000 e que duas cidades, A e B, nesse mapa, estão distantes, entre si, 5 cm, a distância real entre essas cidades é de:

a) 25.000 m

b) 1 .250 m

c) 12.500 m

d) 500 m

e) 250 m

Questão 4 – (UNESP) A escala cartográfica define a proporcionalidade entre a superfície do terreno e sua representação no mapa, podendo ser apresentada de modo gráfico ou numérico.

A escala numérica correspondente à escala gráfica apresentada é:

a) 1:184 500 000.

b) 1:615 000.

c) 1:1 845 000.

d) 1:123 000 000.

e) 1:61 500 000.

Questão 5 – (PUC – RS) INSTRUÇÃO: Imagine que você tem diante de si dois mapas que representam a área urbana do Município de Porto Alegre, de acordo com as escalas seguintes:

• Mapa 1 – escala 1:50.000

• Mapa 2 – escala 1:1.000.000

Com base nesses dados, é correto afirmar que:

a) Em ambos os mapas ocorre uma representação rica em detalhes, o que facilita a leitura dos elementos urbanos que constituem a cidade.

b)A escala do mapa 1 é mais recomendada para planisférios que fazem parte de atlas escolares.

c)Um mapa na escala 1:500 possibilita a representação da área urbana de Porto Alegre com mais detalhes que os mapas 1 e 2.

d)O mapa 2, por ser maior que o mapa 1, é mais favorável à representação de detalhes que este último.

e)A riqueza de detalhes que um mapa pode representar não depende da escala, e sim da qualidade da legenda.

Questão 6 – (Unicamp) Escala, em cartografia, é a relação matemática entre as dimensões reais do objeto e a sua representação no mapa. Assim, em um mapa de escala 1:50.000, uma cidade que tem 4,5 Km de extensão entre seus extremos será representada com

a) 9 cm.

b) 90 cm.

c) 225 mm.

d) 11 mm.

Questão 7 – (UERJ) Naquele Império, a arte da cartografia alcançou tal perfeição que o mapa de uma única província ocupava uma cidade inteira, e o mapa do Império uma província inteira. Com o tempo, estes mapas desmedidos não bastaram e os colégios de cartógrafos levantaram um mapa do Império que tinha o tamanho do Império e coincidia com ele ponto por ponto. Menos dedicadas ao estudo da cartografia, as gerações seguintes decidiram que esse dilatado mapa era inútil e não sem impiedade entregaram-no as inclemências do sol e dos invernos. Nos desertos do oeste perduram despedaçadas ruínas do mapa habitadas por animais e por mendigos.

BORGES, J. L. Sobre o rigor na ciência. Em: História universal da infâmia. Lisboa: Assírio e Alvim, 1982.

No conto de Jorge Luís Borges, apresenta-se uma reflexão sobre as funções da linguagem cartográfica para o conhecimento geográfico.

A compreensão do conto leva à conclusão de que um mapa do tamanho exato do Império se tornava desnecessário pelo seguinte motivo:

a) extensão da grandeza do território político.

b) imprecisão da localização das regiões administrativas.

c) precariedade de instrumentos de orientação tridimensional.

d) equivalência da proporcionalidade da representação espacial.

Respostas dos exercícios de Escala

Exercício resolvido da questão 1 –

Alternativa correta: e) 1 : 25 000 000.

Exercício resolvido da questão 2 –

Alternativa correta: d) 18 cm

Exercício resolvido da questão 3 –

Alternativa correta: b) 1 .250 m

Exercício resolvido da questão 4 –

Alternativa correta: e) 1:61 500 000.

Exercício resolvido da questão 5 –

Alternativa correta:  c)Um mapa na escala 1:500 possibilita a representação da área urbana de Porto Alegre com mais detalhes que os mapas 1 e 2.

Exercício resolvido da questão 6 –

Alternativa correta:  a) 9 cm.

Exercício resolvido da questão 7 –

Alternativa correta: d) equivalência da proporcionalidade da representação espacial.

Estude para o Enem com o Simulado Beduka. É gratuito!

Gostou dos nossos Exercícios de Escala? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.