Está se preparando para o Enem? Então cola com a gente que trouxemos um artigo completo com questões de matemática do Enem. Elas foram selecionadas a dedo, são as melhores! E ainda te contamos os detalhes da prova, como os assuntos que mais caem. Não vai perder o gabarito e resolução no final hein!
Para não se perder em tanta informação boa, dividimos o texto em tópicos. Clique em um deles para ir diretamente ao assunto:
- Como a matemática cai no Enem?
- Quais assuntos mais caem nas questões sobre matemática no Enem?
- Exercícios de Matemática do Enem
- Gabarito e Solução dos exercícios de matemática do Enem!
Não decidiu qual profissão seguir? A gente te ajuda! Faça agora mesmo o Raio-X do Beduka, ele analisa sua personalidade e indica quais cursos combinam com você!
Como a matemática cai no Enem?
Quase todas as questões de matemática do Enem possuem uma pitada de matemática básica e interpretação do enunciado. Contudo, não se engane!
É preciso estar atendo aos detalhes e saber utilizar ferramentas especializadas. Se não, você pode até saber fazer mas não vai conseguir terminar a tempo, pois esta é a matéria que ocupa mais questões!
Para resolver os exercícios do Exame Nacional do Ensino Médio (ENEM) é fundamental saber analisar e compreender. Algumas questões trazem muitos textos, gráficos e tabelas, mas é preciso ficar atento ao que é pedido e interpretar corretamente.
Tudo isso você só consegue com MUITA prática!
Por isso, tem quiz diário e muitos posts interativos no Instagram do Beduka! Você não vai perder a chance de nos seguir lá, né?
Quais são as matérias que mais caem nas questões de matemática no Enem?
As matérias da prova de Matemática e suas Tecnologias mais recorrentes são:
- Funções de 1° e 2° graus
- Equações de 1º e 2º graus
- Trigonometria (triângulo retângulo e semelhança de triângulos)
- Cálculo de área, volume e perímetros
- Seno, cosseno e tangente
- Probabilidade
- Análise combinatória
- Progressão aritmética e geométrica
- Estatística – média aritmética, moda e mediana
- Grandezas proporcionais – inversamente ou diretamente proporcionais, regra de três
- Porcentagem
- Áreas de figuras planas/prismas, cilindros, cones e esferas
- Metro cúbico
Por isso, separamos neste artigo algumas questões de matemática do Enem de cada tema para você ir se familiarizando.
Porém, só elas não bastam para arrasar no Enem. Quando acabar de resolver essas 10, treine com o simulado gratuito e online! Ele pode ser personalizado com a matéria que você quer e possui centenas de questões, com gabarito!
Questões de Matemática do Enem
O grande segredo para se sair bem na prova de Matemática do Enem é resolver as provas anteriores. E se você quiser saber como aprender matemática sozinho, cola com a gente!
Sem mais delongas, vamos às questões de matemática do Enem!
1° das questões de matemática do Enem – 2017
Um morador de uma região metropolitana tem 50% de probabilidade de atrasar-se para o trabalho quando chove na região; caso não chova, sua probabilidade de atraso é de 25%. Para um determinado dia, o serviço de meteorologia estima em 30% a probabilidade da ocorrência de chuva nessa região.
Qual é a probabilidade de esse morador se atrasar para o serviço no dia para o qual foi dada a estimativa de chuva?
a) 0,075
b) 0,150
c) 0,325
d) 0,600
e) 0,800
2° das questões de matemática do Enem – 2013
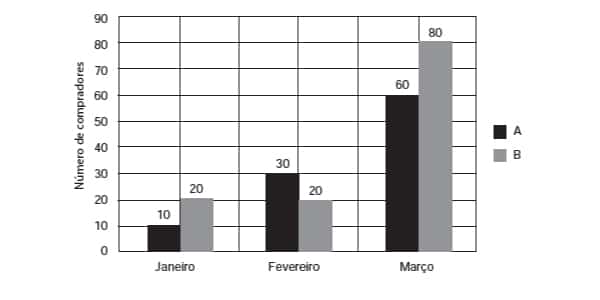
Uma loja acompanhou o número de compradores de dois produtos, A e B, durante os meses de janeiro, fevereiro e março de 2012. Com isso, obteve este gráfico:
A loja sorteará um brinde entre os compradores do produto A e outro brinde entre os compradores do produto B.
Qual a probabilidade de que os dois sorteados tenham feito suas compras em fevereiro de 2012?
a) 1/20
b) 3/242
c) 5/22
d) 6/25
e) 7/15
3° das questões de matemática do Enem – 2012
Alguns objetos, durante a sua fabricação, necessitam passar por um processo de resfriamento. Para que isso ocorra, uma fábrica utiliza um tanque de resfriamento, como mostrado na figura.
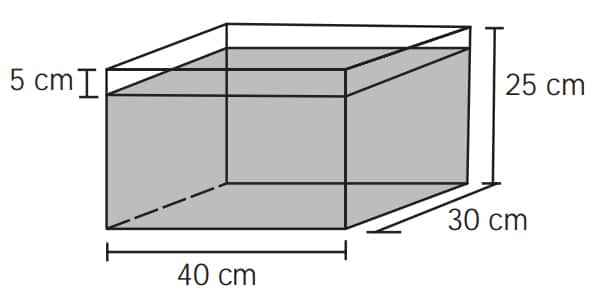
O que aconteceria com o nível da água se colocássemos no tanque um objeto cujo volume fosse de 2 400 cm³?
a) O nível subiria 0,2 cm, fazendo a água ficar com 20,2 cm de altura.
b) O nível subiria 1 cm, fazendo a água ficar com 21 cm de altura.
c) O nível subiria 2 cm, fazendo a água ficar com 22 cm de altura.
d) O nível subiria 8 cm, fazendo a água transbordar.
e) O nível subiria 20 cm, fazendo a água transbordar.
4° das questões de matemática do Enem – 2018
A figura mostra uma praça circular que contém um chafariz em seu centro e, em seu entorno, um passeio. Os círculos que definem a praça e o chafariz são concêntricos.
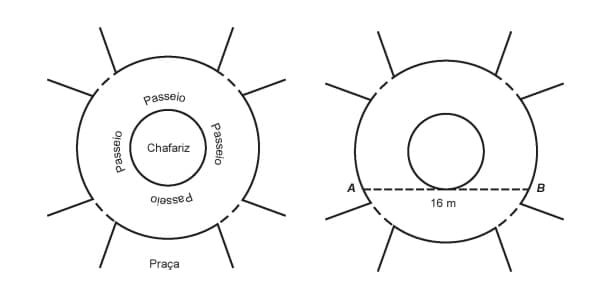
O passeio terá seu piso revestido com ladrilhos. Sem condições de calcular os raios, pois o chafariz está cheio, um engenheiro fez a seguinte medição: esticou uma trena tangente ao chafariz, medindo a distância entre dois pontos A e B, conforme a figura. Com isso, obteve a medida do segmento de reta AB: 16 m.
Dispondo apenas dessa medida, o engenheiro calculou corretamente a medida da área do passeio, em metro quadrado. A medida encontrada pelo engenheiro foi
a) 4π
b) 8π
c) 48π
d) 64π
e) 192π
5° das questões de matemática do Enem – 2017
Os congestionamentos de trânsito constituem um problema que aflige, todos os dias, milhares de motoristas brasileiros. O gráfico ilustra a situação, representando, ao longo de um intervalo definido de tempo, a variação da velocidade de um veículo durante um congestionamento.
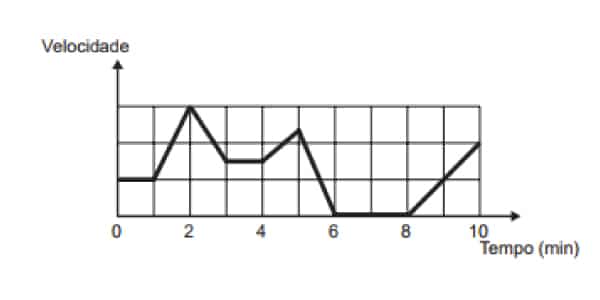
Quantos minutos o veículo permaneceu imóvel ao longo do intervalo de tempo total analisado?
a) 4
b) 3
c) 2
d) 1
e) 0
6° das questões de matemática do Enem – 2013
A parte interior de uma taça foi gerada pela rotação de uma parábola em torno de um eixo z, conforme mostra a figura.
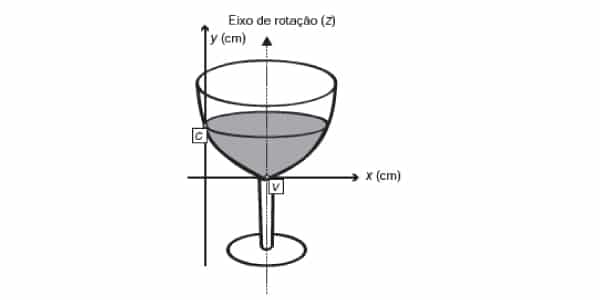
A função real que expressa a parábola, no plano cartesiano da figura, é dada pela lei onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x.
Nessas condições, a altura do líquido contido na taça, em centímetros, é
a) 1
b) 2
c) 4
d) 5
e) 6
7° das questões de matemática do Enem – 2014
Uma criança deseja criar triângulos utilizando palitos de fósforo de mesmo comprimento. Cada triângulo será construído com exatamente 17 palitos e pelo menos um dos lados do triângulo deve ter o comprimento de exatamente 6 palitos. A figura ilustra um triângulo construído com essas características.
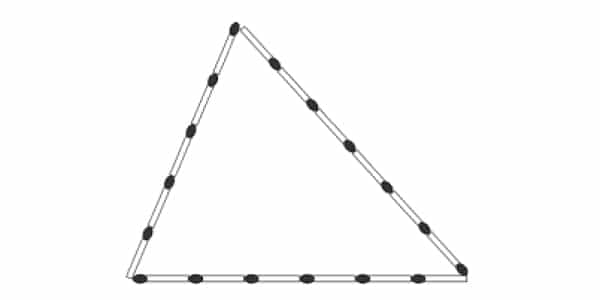
A quantidade máxima de triângulos não congruentes dois a dois que podem ser construídos é:
a) 3
b) 5
c) 6
d) 8
e) 10
8° das questões de matemática do Enem – 2013
O dono de um sítio pretende colocar uma haste de sustentação para melhor firmar dois postes de comprimentos iguais a 6m e 4m. A figura representa a situação real na qual os postes são descritos pelos segmentos AC e BD e a haste é representada pelo segmento EF, todos perpendiculares ao solo, que é indicado pelo segmento de reta AB. Os segmentos AD e BC representam cabos de aço que serão instalados.
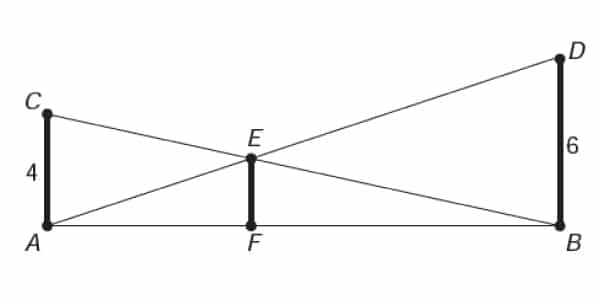
Qual deve ser o valor do comprimento da haste EF?
a) 1 m
b) 2 m
c) 2,4 m
d) 3 m
e) 2√6 m
9° das questões de matemática do Enem – 2011
Para determinar a distância de um barco até a praia, um navegante utilizou o seguinte procedimento: a partir de um ponto A, mediu o ângulo visual a fazendo mira em um ponto fixo P da praia. Mantendo o barco no mesmo sentido, ele seguiu até um ponto B de modo que fosse possível ver o mesmo ponto P da praia, no entanto sob um ângulo visual 2α . A figura ilustra essa situação:
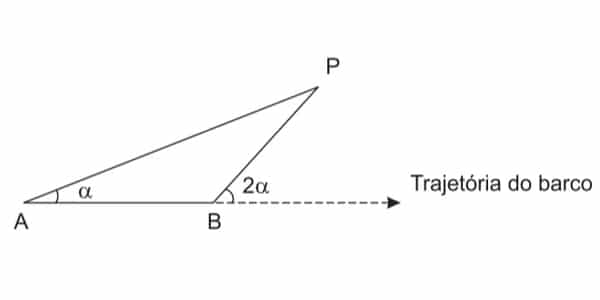
Suponha que o navegante tenha medido o ângulo α=30o e, ao chegar ao ponto B, verificou que o barco havia percorrido a distância AB=2000m . Com base nesses dados e mantendo a mesma trajetória, a menor distância do barco até o ponto fixo P será:
a) 1 000 m.
b) 1 000 √3 m.
c) 2 000 √3/3 m.
d) 2000 m
e) 2 000 √3 m.
10° das questões de matemática do Enem – 2016
Em 2011, um terremoto de magnitude 9,0 na escala Richter causou um devastador tsunami no Japão, provocando um alerta na usina nuclear de Fukushima. Em 2013, outro terremoto, de magnitude 7,0 na mesma escala, sacudiu Sichuan (sudoeste da China), deixando centenas de mortos e milhares de feridos. A magnitude de um terremoto na escala Richter pode ser calculada por
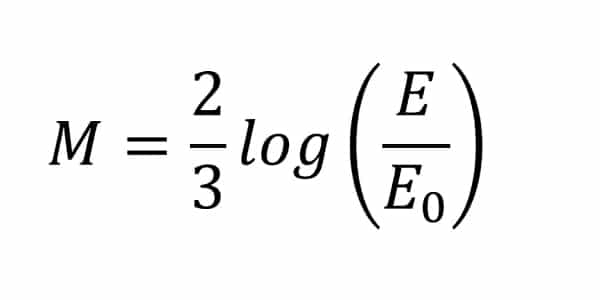
sendo E a energia, em kWh, liberada pelo terremoto e E0 uma constante real positiva. Considere que E1 e E2 representam as energias liberadas nos terremotos ocorridos no Japão e na China, respectivamente.
Disponível em: www.terra.com.br. Acesso em: 15 ago. 2013 (adaptado).
Qual a relação entre E1 e E2?
a) E1 = E2 + 2
b) E1 = 10².E2
c) E1 = 10³.E2
d) E1 = 109/7.E2
e) E1 = 9/7.E2
Gabarito e Resolução das questões sobre matemática do Enem
Solução do 1° exercício de matemática do Enem – 2017
Solução do 2° exercício de matemática do Enem – 2013
Solução do 3° exercício de matemática do Enem – 2012
Solução do 4° exercício de matemática do Enem – 2018
Solução do 5° exercício de matemática do Enem – 2017
Solução do 6° exercício de matemática do Enem – 2013
Solução do 7° exercício de matemática do Enem – 2014
Solução do 8° exercício de matemática do Enem – 2013
Solução do 9° exercício de matemática do Enem – 2011
Solução do 10° exercício de matemática do Enem – 2016
Gostou do nosso artigo sobre as questões de matemática do Enem? Nós queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender!





