Entenda a Escala Matemática! Saiba calcular, entender o símbolo, exemplos e tipos!

A Escala Matemática é uma razão entre medidas reais e representativas. Ela leva em conta a proporção que há entre as distâncias de um desenho e da realidade, por exemplo. Ela é muito utilizada em mapas e na geografia ganha o nome de escala cartográfica. Alguns exemplos são 1:100, significando que 1 unidade no desenho equivale a 100 do real.

Neste artigo sobre Escala Matemática, você encontrará:

1. O que é Escala Matemática?
2. O que é Razão e proporção?
3. Como calcular escala? Exemplos resolvidos e fórmula
4. Tipos de escala: cartográfica, natural, reduzida, ampliada, grande, pequena

• Confira os exercícios de escala ao terminar sua leitura, para treinar o que aprendeu!

• Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!

O que é Escala Matemática?

A Escala é uma fórmula da razão que há entre medidas proporcionais. Ela é uma constante que nos permitirá comparar as medidas de uma situação real com a sua representação.

As distâncias representadas em miniaturas, esculturas não-realistas, mapas, plantas e maquetes são apenas a representação de algo do mundo real. Para manter a proporção do que se deseja representar, utilizamos um cálculo matemático bem simples, chamado escala!

Não entendeu ainda? Vamos relembrar os conceitos de razão e proporção, vendo um exemplo:

O que é Razão e Proporção?

Vamos supor que uma parede mede 10m na vida real e está representada na maquete com 1m. Já a árvore mede 2m na vida real e está na maquete com 0,2m. 

Se compararmos a relação que existe entre a árvore e a parede, ela será a mesma, seja na maquete ou na vida real, veja:

• 10m (parede real) / 2m (árvore real) = 5 , ou seja, a árvore é 5x menor que a parede, na realidade.
• 1m (parede maquete) / 0,2m (árvore maquete) = 5 , ou seja, a árvore permanece 5x menor que a parede na representação.

Isso ocorre porque mesmo sendo representadas em outra dimensão (real ou representativa) a razão de proporcionalidade permaneceu a mesma, ao se fazer a transformação do objeto real na representação:

• 10m (parede real) / 1m (parede maquete) = 10
• 2m (árvore real) / 0,2m (árvore maquete) = 10.

Assim, a proporção é manter as coisas equidistantes entre si, ainda que se amplie o objeto ou o diminua. A razão é a divisão que se faz entre o objeto real e sua representação, para averiguar de quanto foi essa mudança.

Mas o que a escala tem a ver com isso? 

Ela é justamente a fórmula que irá representar todos esses dados! Vamos ver alguns exemplos e aprender a lê-las e calcular:

Como calcular Escala? Veja a Fórmula! 

Uma escala se apresenta sempre pelo número um seguido de dois pontos e um número específico depois. Dessa forma:

• 1: 100

A forma como lemos isso é:

• “1 unidade na representação equivale a 100 unidades na realidade”

Sempre o primeiro número refere-se ao desenho e o segundo a sua equivalência na vida real.

Assim, lembrando do significado de razão , podemos dizer que os dois pontos indicam uma divisão, e teremos a seguinte fórmula:

• Escala = medida do desenho / medida do real

Como você viu, podemos escrever em forma de fração, e daí vem a explicação de o primeiro número ser o 1, porque fazemos uma simplificação! Mas se você vir algo como 3:6 não se preocupe, o modo como fazemos a leitura é sempre o mesmo!

Por fim, é importante ressaltar que quando não houver indicação de unidade de medida, sempre consideramos o cm. Mas, se o primeiro número estiver em centímetros e o segundo em metros, precisamos fazer a conversão de tudo para a mesma unidade!

Exemplos de cálculos resolvidos

1.Vamos supor que em um mapa a legenda seja a seguinte 1 cm : 500 km. Como foi dito, lemos essa escala da seguinte maneira: um centímetro está para quinhentos quilômetros. Ou seja, cada centímetro de distância no mapa corresponde a quinhentos quilômetros na realidade. 

Se utilizarmos uma régua e medirmos a distância entre duas cidades no mapa, e obtermos 2 cm, poderemos calcular qual a distância real entre as cidades. Para isso, basta fazer uma regra de três!

1 cm – 500 km

2 cm – x km

Assim, percebemos que a distância real entre as cidades é de 1000 km!

2. Um escultor disse que viu uma maçã que media 10 cm de altura, mas na hora de fazer sua escultura, resolveu fazer uma miniatura com 2 cm de altura. Descubra qual foi a escala que o artista utilizou!

Aqui, basta aplicar a fórmula: 10/2 = 5 , ou seja, escala 1:5.

Tipos de Escala Matemática

Existem alguns tipos de escala dependendo de como fica o desenho final de sua representação ou de qual o contexto em que é aplicada. Vamos conhecê-las:

Escala natural

É aquela representada numericamente como 1:1 ou 1/1. Ela só acontece quando o tamanho do objeto real é igual ao da representação.

Escala reduzida: 

Ocorre quando queremos diminuir a representação do objeto real. É a mais utilizada nos mapas e a que trabalhamos nos exemplos acima e na maioria das questões. Exemplos: 1:2, 1:5, 1:10, 1:20, 1:50, 1:100, 1:500, 1:1000, 1:5000, 1:20000.

Escala ampliada

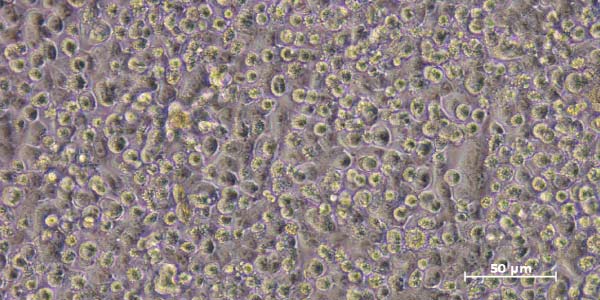
Ocorre quando queremos ampliar a representação do objeto real. É usada para mostrar detalhes mínimos de determinada área, como imagens de microscópio. Exemplos: 50:1, 100:1, 400:1, 1000:1.

Escala cartográfica ou geográfica

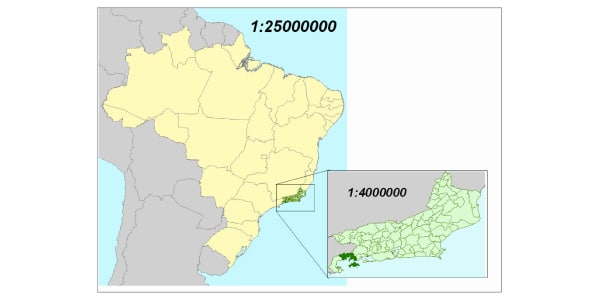
As escalas estão diretamente ligadas aos estudos da Geografia para a construção de mapas e na Engenharia e na Arquitetura para confecção de maquetes e plantas). Além disso, na Navegação Marítima e Aérea e nas táticas militares também!

Mas, toda vez que falarmos em mapas, a escala ganhará o apelidinho especial de cartográfica, pois a ciência que estuda mapas se chama cartografia. O seu cálculo se mantém exatamente o mesmo!

Escala Gráfica

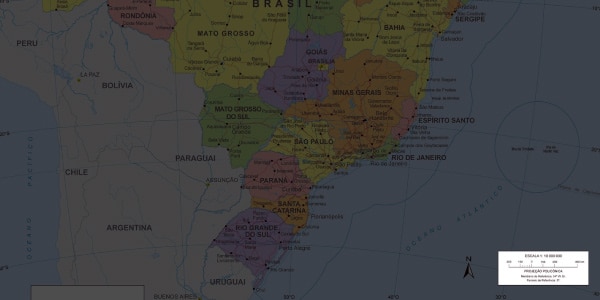
É aquela em que não existe a fórmula com os dois pontos, mas um desenho gráfico de uma régua indicando a medida que aquele distância ali marcada vale. É muito comum em mapas.

Escala grande e pequena

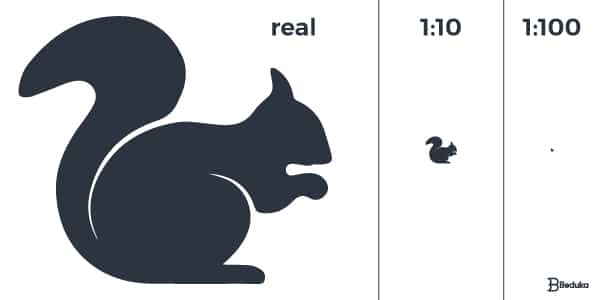
Como se trata de uma divisão, quando queremos comparar qual escala é maior ou menor que a outra, precisamos ter um raciocínio inverso! 

Dizemos que uma escala é pequena quando os seus números são maiores. Isso acontece porque quanto maior for o denominador da divisão, menor o resultado. Consequentemente, o objeto representado fica pequeno. Ex: 1:100

Dizemos que uma escala é grande quando os seus números são menores. Isso acontece porque quanto menor for o denominador, maior o resultado. Assim, o objeto representado não fica tão pequeno. Ex: 1:10

Lembre-se de retornar ao início do artigo e clicar no link dos exercícios!

Gostou do nosso artigo sobre Escala Matemática? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.

Experimente agora!