A Função Constante é aquela que resulta no mesmo valor, independe de qual número colocarmos em “x”. Dessa forma, seu valor final sempre será uma constante “k”, responsável por definir a altura que a reta ocupará no gráfico. Sua principal característica é ter a reta sempre paralela ao eixo x.
Neste artigo, você encontrará:
- Introdução: o que é constante e o que é função?
- O que é uma Função Constante? Fórmula, definição e diagrama de flechas
- Como saber se a função é constante?
- Gráfico e resolução de questões
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
Introdução e Conceitos Importantes
Antes de estudarmos a Função Constante propriamente dita, vamos relembrar conceitos importantes. Se você já sabe, pule para o próximo tópico!
O que é uma Constante?
Uma constante é um elemento numérico que apresentará sempre o mesmo valor, independe do contexto em que for aplicada!
Parece sem sentido? Veja este exemplo:
Você já deve ter ouvido falar na constante gravitacional, também conhecida simplesmente como gravidade! Todos nós estudamos na física que a gravidade da Terra tem o mesmo valor em qualquer ponto do planeta!
Por isso, você continua tendo o mesmo peso (e os pés no chão, sem flutuar) independente da altura em que se encontra: seja numa caverna do Chile ou no topo dos Alpes Suíços.
Se você fosse para a Lua, teria um peso diferente em relação à Terra, mas ele se manteria constante em qualquer ponto dentro da Lua!
O que é uma função?
As funções matemáticas são expressões numéricas e algébricas (números e letras) que possuem dois lados separados pelo sinal de igual (=) e obedecem uma regra, chamada lei de formação.
Quando usamos a expressão “em função de”, traz uma ideia de relação entre as coisas. Portanto, ser uma função significa ter dependência, ou seja, o valor da função “f(x)” ou “y” se modifica à medida que modificamos o valor de “x”.
Essa ideia é o básico de qualquer função. O que muda são as consequências numéricas que cada tipo de lei de formação e as formas de seus gráficos.
- Se você está iniciando no assunto ou quiser se aprofundar no mundo das funções, veja o nosso artigo completo sobre o que são Funções Matemáticas!
O que é uma Função Constante?
A função constante é aquela caracterizada pela fórmula:
- f(x) = k
Na qual:
X = Domínio, ou seja, todas as possibilidades que podemos colocar para calcular o valor final.
F(x) = Valor final da função de acordo com cada valor de x
K = Símbolo universal para constantes, ou seja, para um valor que sempre vale o mesmo.
Isso significa que, independente do valor que colocarmos em x, o resultado final sempre será o mesmo. Como resultado disso, o seu gráfico será uma reta que passa sempre pelo mesmo valor.
Diagrama de Flechas
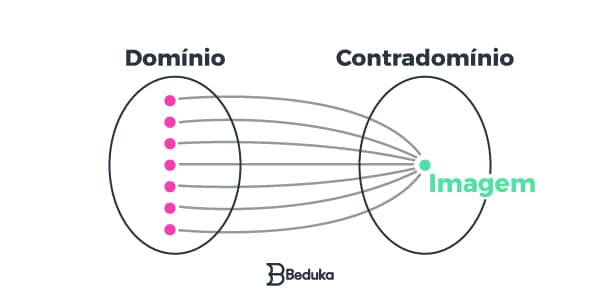
No artigo em que estudamos as Funções Matemáticas, entendemos a ideia de Domínio, Contradomínio e Imagem. Dessa forma, o diagrama de flechas desse tipo de função seria como o representado acima.
Assim, independente dos valores pertencentes ao Domínio, a Imagem é sempre composta por um único elemento.
Como saber se a função é constante?
A melhor forma de saber se uma função é constante é pelo seu gráfico, que tem a característica de ser uma reta paralela ao eixo x.
Por outro lado, basta você supor alguns valores para x e colocá-lo na fórmula. Resolvendo corretamente a conta para cada valor, você verá que o valor final não muda.
A seguir, vamos entender melhor essa questão do gráfico e da resolução da conta:
Gráfico da Função Constante
Como já foi dito, o gráfico da Função Constante sempre será o desenho de uma reta horizontal, ou seja, paralela ao eixo das abscissas (eixo x). Dessa forma, essa função nunca será classificada como crescente ou decrescente.
O que varia é a posição da reta em relação ao ponto que cortar o eixo das coordenadas (eixo y). Isso ocorre porque uma função de lei I resulta na constante 5 e a função de lei II resulta na constante 3. Assim, as retas são parecidas, mas cada uma está em certa “altura” no plano cartesiano.
Para entender melhor, vamos construir juntos o gráfico de 3 Funções Constantes:
Construção do Gráfico e Resolução de Exercícios
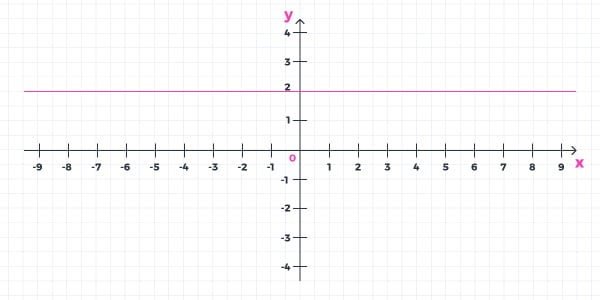
- Exemplo 1: Construa o gráfico da função f(x) = 2.
Pela própria forma da lei de formação, podemos deduzir que é uma função constante. Portanto, o “x” pode assumir qualquer valor que o resultado “y” sempre valerá 2. Assim, temos o seguinte gráfico:
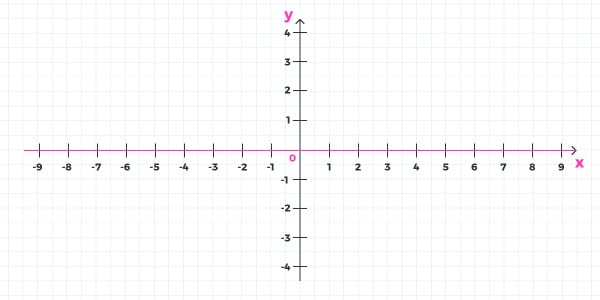
- Exemplo 2: construa o gráfico da função f(x) = 0.
Este exemplo é muito semelhante ao acima, contudo, dizemos que esta reta é coincidente ao eixo x, porque intercepta o eixo y na origem (0). Assim, o gráfico será:
- Exemplo 3: construa o gráfico da função f(x) = – 2x – 8 / x + 4
À primeira vista, não conseguimos identificar o tipo de função só pela lei de formação. Contudo, podemos chegar a conclusão de 2 formas: ou simplificamos a lei algébrica, ou estipulamos valores para x e vamos resolvendo normalmente.
No primeiro modo de resolução, teríamos:
Coloque o –2 em evidência no numerador e realize as operações corretamente. Depois, simplifique o resultado e restará apenas o valor da constante. Assim:
f(x) = -2x – 8 / x + 4
f(x) = -2 . (x + 4) / x + 4
f(x) = -2
Escrevendo essa mesma lei de formação em outras palavras, teríamos: f(x) = -2.
No segundo modo de resolução, teríamos:
Supondo os valores de x: -2, -1, 0, 1 e 2. Substituindo-os na fórmula inicial e resolvendo a conta, teríamos os resultados:
Para x = -2
f(x) = -2 . (-2) – 8 / -2 + 4
f(x) = 4 – 8 / 2
f(x) = -4 / 2
f(x) = -2
Para x = -1
f(x) = -2 . (-1) – 8 / -1 + 4
f(x) = 2 – 8 / 3
f(x) = – 6 / 3
f(x) = – 2
Para x = 0
f(x) = -2 . (0) – 8 / 0 + 4
f(x) = -8 / 4
f(x) = -2
Para x = 1
f(x) = -2 . (1) – 8 / 1 + 4
f(x) = -2 – 8 / 5
f(x) = -10 / 5
f(x) = -2
Para x = 2
f(x) = -2 . (2) – 8/ 2 + 4
f(x) = -4 -8 / 6
f(x) = -12 / 6
f(x) = -2
Portanto, de ambas as formas teríamos o mesmo gráfico:
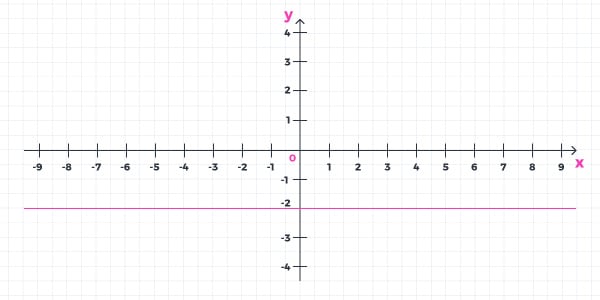
Gostou do nosso artigo sobre Função Constante? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





