Sólido geométrico, de revolução ou corpo redondo… Esses são os vários nomes que classificam o Cilindro. Ele é tão diverso que existem 3 tipos de cilindros, 3 fórmulas de área, a de volume, as planificações e as definições (formais ou simples). Neste resumo de Cilindro, você terá o material mais completo e objetivo sobre o assunto!
Neste resumo de Cilindro, você encontrará os tópicos abaixo. Se quiser, clique em um deles para ir diretamente ao conteúdo:
- Introdução: O que é a Geometria Espacial?
- Definição formal e simples: o que é um Cilindro?
- Quais são os elementos do Cilindro?
- Origem do Cilindro: Planificação e Rotação.
- Como são as Seções Transversais e Meridionais?
- Quais são os 3 principais tipos de Cilindros?
- Fórmulas do Cilindro: áreas e volume.
Depois você pode testar o que aprendeu. É só fazer o nosso Simulado ENEM gratuito! Ele pode ser personalizado com as matérias que você quiser.
Introdução: o que é a Geometria Espacial?
A Geometria Espacial é a área da matemática que estuda os sólidos geométricos. Estamos falando daquelas formas que construímos com 3 dimensões (3D): altura, largura e profundidade.
Quando pegamos um sólido (que é tridimensional), é preciso girar em várias posições para tatear toda a sua superfície. Quando pegamos uma figura plana, existe uma só superfície.
Os sólidos podem ser classificados em poliedros (faces, arestas e vértices, tudo retinho) ou corpos redondos (possui alguma superfície curva).
Hoje nós vamos falar do Cilindro, que é um dos corpos redondos. Isso significa que ele pertence ao grupo dos que “rolam” ao serem colocados em algum plano inclinado.
Antes de continuar, vale a pena lembrar da Geometria Plana, a parte que estuda as figuras 2D (largura e altura). É nela que estudamos os conceitos básicos (reta, linha, ponto, plano, altura, etc.) que também usaremos adiante.
Definição: o que é um Cilindro?
A definição formal de Cilindro é a seguinte:
“Dados dois planos paralelos α e β, um círculo C no plano α e uma reta r secante a esses planos, um cilindro é o conjunto de segmentos paralelos a r que possuem como extremidade o círculo C no plano α e algum ponto do plano β.”
Não entendeu nada? Vamos explicar de uma forma mais simples:
O Cilindro é formado por dois círculos que estão em planos distintos e paralelos. Isso significa que um círculo está acima do outro e que estão alinhados, possuindo a mesma inclinação.
Assim, o espaço que há entre as bases circulares é preenchido pelo conjunto de segmentos de reta. Esses traços ligam todos os pontos do círculo de cima com os do de baixo.
É importante lembrar que esses segmentos são paralelos e congruentes (mesmo valor). Além disso, os círculos das bases possuem os mesmo valores de raio e diâmetro.
- Como descrever um cilindro para alguém?
Se você quer falar do cilindro de uma forma mais simples, pode dizer:
“O cilindro é um sólido geométrico alongado e arredondado. Ele tem duas bases circulares e o seu diâmetro é o mesmo ao longo de todo o comprimento.”
Quais são os principais componentes do Cilindro?
Entender as definições são tarefas trabalhosas, mas conhecer os elementos do Cilindro vão te ajudar a entendê-lo. Seus componentes são:
- Raio (r): o raio do cilindro é o mesmo que os raios das bases circulares. Sendo assim, definimos como a distância entre o centro do cilindro e a sua face externa.
- Diâmetro (D): é a medida que liga duas extremidades do círculo, passando pelo centro. Na prática, vale o dobro do raio (2r).
- Base: no caso do cilindro, são os dois planos em que estão as circunferências, sendo uma em cima e outra embaixo. Elas são superfícies retas (passamos a mão e está “liso”).
- Altura (h): é, literalmente, quanto mede a altura do cilindro. Na geometria, definimos como um segmento que liga o centro da base de cima com a superfície em que a figura está apoiada, embaixo, fazendo um ângulo de 90°. A altura também pode ser definida como a distância entre os planos α e β, em que estão os círculos das bases.
- Geratriz (g): é o segmento que liga o ponto mais externo do círculo da base de cima com o ponto alinhado da base de baixo. Assim, forma uma linha que passa na superfície do cilindro. Normalmente, ela tem o mesmo valor que a altura.
- Diretriz: corresponde à curva do plano da base.
Note que o cilindro possui três faces (duas bases e toda a parte curva no meio), mas não possui nenhuma aresta e nenhum vértice.
- São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!
Como surgiu o cilindro?
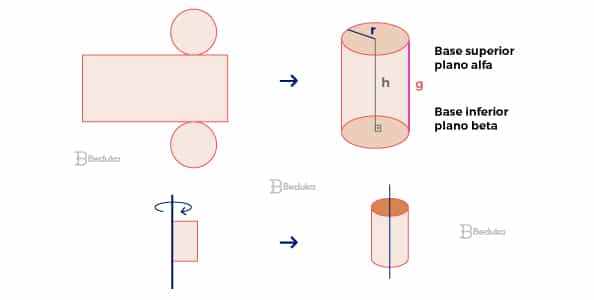
O cilindro pode surgir por meio de dois processos: Planificação e Revolução. Leia e aprenda sobre cada um deles:
O que é a planificação do cilindro?
Na infância, é comum as escolas pedirem que os alunos façam sólidos geométricos. Você já fez isso, não fez?
O que os professores nos pedem é, justamente, montar o sólido a partir de sua planificação.
A planificação é a tentativa de projetar uma figura tridimensional em um plano bidimensional, mostrando todas as suas partes ao mesmo tempo.
Para conseguir, é preciso ter boa visão espacial. Isso significa olhar para o conjunto de figuras planas e imaginar que você tirou do papel, cortou, dobrou, colou e conseguiu formar um sólido.
No caso do cilindro, as planificações são formadas por dois tipos de figuras planas: os círculos e os retângulos. Os círculos formam a base e o retângulo, após ser “enrolado”, forma a superfície curva.
Essa visão nos permite encontrar uma relação importante na hora de resolver os exercícios:
Na planificação dos cilindros, a largura do retângulo mede o mesmo que o comprimento da circunferência.
O que é a Revolução dos Cilindros?
Alguns dos sólidos geométricos podem receber o nome de “sólidos de revolução”.
Calma! Você nunca vai ver um exército de cilindros pegar em tochas e forcados para lutar pelos direitos. Isso você vê no nosso artigo sobre Revolução Russa. Aqui o assunto é outro…
Esse título vem da ideia de que podemos pegar uma figura plana, colocá-la em uma bandeja giratória e rodá-la.
Se colocarmos um retângulo e giramos em altíssima velocidade, o vulto que se formará será no formato de um cilindro. Portanto, o cilindro é um sólido de rotação que se origina por um retângulo.
Como são as Seções no Cilindro?
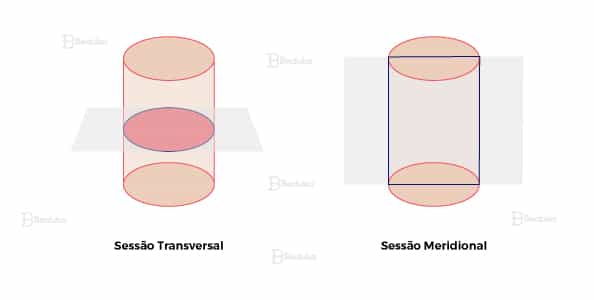
Existe uma prática comum na geometria espacial que é a de fazer seções (cortes) nos sólidos. É como se passássemos uma lâmina em diferentes ângulos para ver qual figura se forma na superfície do corte.
Não por coincidência, existem dois possíveis cortes que podemos fazer no cilindro, que originam superfícies circulares e retangulares.
- Secção Transversal: é a intersecção entre o sólido e um plano horizontal (paralelo às bases). A figura formada em um cilindro será um círculo congruente às bases.
- Secção Meridional: é a intersecção entre o sólido e um plano vertical (contém o eixo). A figura formada em um cilindro será um retângulo.
Quais os tipos de cilindros que existem?

Por incrível que pareça, há diferentes formatos de cilindros, dependendo da inclinação de seu eixo ou da relação entre suas medidas.
Há três tipos principais:
- Cilindro Reto: quando suas geratrizes são perpendiculares às bases (g=h).
- Cilindro Oblíquo: quando as geratrizes não são perpendiculares à base, formam outro ângulo inclinado (g≠h).
- Cilindro Equilátero: é o tipo de cilindro em que a altura é igual ao diâmetro (h=2r), fazendo com que a sessão meridional seja um quadrado, não um retângulo.
Como calcular área e volume no Cilindro?
Ao lidar com sólidos geométricos, podemos calcular:
- Área da base: valor do preenchimento da superfície das bases.
- Área lateral: valor do preenchimento da superfície que “rola”.
- Área total: soma das duas anteriores.
- Volume: o preenchimento interno do sólido, como o quanto de água que cabe dentro.
Vamos conhecer as fórmulas para calcular as áreas e o volume do cilindro:
Fórmula das áreas do Cilindro
- Área de uma das bases:
Ab = π.r²
Em que:
Ab: área da base
π: 3,14
r: raio
- Área Lateral:
Al = 2 π.r.h
Em que:
Al: área lateral
π: 3,14
r: raio
h: altura
- Área Total:
At = 2.Ab + Al
ou
At = 2(π.r²) + (2 π.r.h)
Onde:
At: área total
Ab: área da base
Al: área lateral
π: 3,14
r: raio
h: altura
Fórmula do Volume do Cilindro
O volume de qualquer sólido com duas bases, seja poligonal ou corpo redondo, é dado pelo produto da área da base pela altura (geratriz). Sendo assim:
V = Ab.h
ou
V = π.r².h
Onde:
V: volume
Ab: área da base
π: 3,14
r: raio
h: altura
Gostou do nosso resumo de Cilindro? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





