Resumo de Função Inversa com exemplos resolvidos!

A função inversa costuma gerar dúvida, mas o próprio nome já nos dá uma dica de como lidar. Neste resumo de Função Inversa, você vai aprender as características dessa função e como calculá-la em apenas 2 passos. Leia e veja os exemplos!

Neste texto com o resumo de Função Inversa, você encontrará os tópicos abaixo. Se quiser, clique em um deles para ir diretamente ao conteúdo:

1. O que é uma função? (definição, elementos e tipos).
2. O que é uma Função Inversa?
3. Quais são as características de uma Função Inversa?
4. Como encontrar o inverso de uma função? + Exemplo.
5. Como construir o gráfico da Função Inversa? + Exemplo.

Depois você pode testar o que aprendeu, é só fazer o nosso Simulado ENEM gratuito! Ele pode ser personalizado com as matérias que você quiser.

O que é uma função?

Para entender o resumo de função inversa, antes precisamos entender o básico de qualquer função!

Sendo assim, as funções matemáticas são expressões numéricas e algébricas que obedecem uma regra, a lei de formação.

Elas possuem dois lados separados pelo sinal de igual (=):

De um lado temos o “f(x)” que representa o valor final da função. Esse valor também pode ser escrito como “y”.

Do outro, temos a regra matemática, ou seja, um conjunto de números que rodeiam o valor “x” e determinam a “cara” daquela função.

Quando usamos a expressão “em função de”, dá uma ideia de relação entre as coisas. Portanto, ser uma função significa ter dependência, ou seja, o valor da função “f(x)” ou “y” se modifica à medida que modificamos o valor de “x”.

Por isso, devemos resolver as funções pensando nos pares ordenados (x,y) que se adequam àquela regra.

Quais são os elementos da função?

Toda função pode ser descrita tendo três elementos. Para compreender este resumo de função inversa, você precisa conhecê-los:

• Domínio (D): conjunto dos valores que podemos colocar em “x”.
• Contradomínio (CD): conjunto de todos os valores possíveis de serem gerados.
• Imagem (I): valores do CD que satisfazem a função, ou seja, são os verdadeiros “y” de cada “x”.

São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!

Tipos de função de acordo com seus elementos

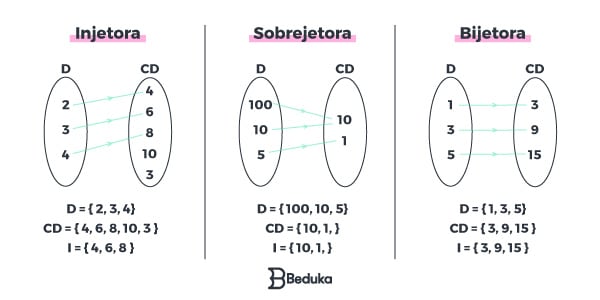
Dependendo de como esses elementos se relacionam, podemos classificar as funções em três tipos: injetora, sobrejetora e bijetora.

Vamos relembrar o que significa cada uma delas, pois precisamos desses conceitos para entender o que é uma função inversa!

O que é uma função Injetora?

A função Injetora é aquela em que cada elemento do Domínio possui um único elemento na Imagem, e vice-versa. Porém, podem existir elementos do Contradomínio que não são Imagem. Eles sobram no conjunto.

Portanto, a Imagem é diferente do Contradomínio.

O que é uma função Sobrejetora?

A função Sobrejetora é aquela em que cada elemento do Domínio possui um elemento na Imagem. Pode acontecer de dois elementos do Domínio possuírem uma mesma Imagem. O que não pode, é um elemento do Domínio possuir 2 imagens. 

Dessa forma, Imagem e Contradomínio são iguais. Não há sobra.

O que é uma função bijetora?

A função Bijetora recebe esse nome porque é injetora e sobrejetora ao mesmo tempo, ou seja, pega uma característica de cada.

Sendo assim, ela é aquela em que cada elemento do Domínio possui um único elemento na Imagem (e vice-versa) e não sobra nada no Contradomínio. 

Isso significa que determinado valor de “x” só pode resultar em um “y”, bem como um resultado “y” sempre corresponde a um valor específico de “x”.

O que é uma Função Inversa?

Como o seu próprio nome indica, a Função Inversa ou Invertível é o inverso de uma uma função f(x). Sendo assim, ela pode ser sinalizada como:

 f(x)^-1

Isso significa que se uma função tem uma operação de soma na sua lei de formação, a função inversa será dada pela subtração. 

Mais um exemplo: se outra função faz com que os valores de x dobrem, a sua função inversa fará o contrário (o valor será dividido por 2).

Observe que a função inversa vem de uma derivação, então estamos criando uma função que vem de outra. Por isso, ambas estão relacionadas e são equivalentes, só que ao inverso.

Quais são as características de uma Função Invertível?

Agora que você já se familiarizou com os conceitos, saiba que as principais características da função inversa são:

Toda Função Inversa precisa ser Bijetora (aquela em que cada elemento do D se liga a somente um elemento do CD e vice-versa, sendo CD = I). Se não fosse assim, não seria possível fazer uma inversão correta e equivalente.

Levando isso em conta, podemos fazer algumas representações das condições que devem haver para que uma função seja inversível. Veja:

Seja a função f representada pelos elementos domínio (A) e imagem (B):

f(x) = y

f : A → B

A inversa da função f(x) é representada da seguinte forma:

f(x)^-1= y

f^-1(y) = x

f^-1: B → A

Qual é o domínio da Função Inversa?

Todas essas representações só querem dizer uma coisa: o domínio da função original será o contradomínio da função inversa. Por isso mesmo, o domínio da função inversa equivale ao contradomínio da função original.

Ficou confuso? Respire e se acalme. 

Vamos sair da teoria e ir para a prática. Assim você consegue enxergar os exemplos concretos e entender melhor!

Encontre inverso de uma função em 2 passos!

Para determinar a função inversa, precisamos compreender bem o conceito dela e com qual domínio e contradomínio estamos trabalhando! Isso porque devemos ter certeza de que ela é bijetora!

Tendo essa certeza, só nos resta tomar 2 passos práticos:

• 1° Passo: para conseguirmos encontrar a lei de formação de uma função inversa, precisamos inverter as incógnitas. Assim, vamos trocar “x por y” e “y por x”. 
• 2° Passo: precisamos isolar a incógnita “y” no primeiro membro e colocar os demais componentes no segundo. 

Depois de seguir esses dois passos simples, já teremos uma nova lei de formação prontinha!

Simples, não é?

Confira um exemplo para facilitar ainda mais:

Exemplo

1) Dada a função f(x) = 2x – 3, calcule a sua inversa.

Resolução:

1° passo: trocar incógnitas:

f(x) = 2x – 3

y = 2x – 3

x = 2y – 3

2° passo: isolar o “y”:

x = 2y – 3

-2y = -3 – x (-1)

2y = 3 + x

y = (3+x) / 2

y = 3/2 + x/2

Assim, o inverso de f(x) = 2x – 3 é dado por f(x)-1 = 3/2 + x/2.

Só tem um detalhe:

Dependendo de qual função for formada na inversa, você deverá resolvê-la de acordo com o seu tipo. Existem métodos próprios para as de 1° grau, 2° grau, exponencial, logarítmica, etc.

Como construir o gráfico de uma Função Inversa?

O gráfico de uma função inversa sempre será a inversão do gráfico da função original. Isso significa que ele será simétrico, como se estivesse espelhado. Assim, os pontos correspondentes de cada função são equidistantes.

É bom saber disso porque às vezes pode ser dado apenas o gráfico, não sua lei de formação. Assim, por ele conseguimos analisar se é crescente, decrescente, etc.

Para formar o gráfico de qualquer função é muito simples:

• 1° Passo: estipule de 3 a 5 valores diferentes para x e jogue-os na função. Calcule para ver qual o resultado de y em cada um deles. Anote os pares ordenados formados (x, y).
• 2° Passo: trace a função original no plano cartesiano seguindo os pares ordenados que foram anotados.
• 3° Passo: calcule o inverso da função e obtenha sua nova lei de formação.
• 4° Passo: repita o primeiro passo, só que usando a lei de formação da função inversa.
• 5° Passo: com os novos pares ordenados resultantes, trace a função inversa no mesmo plano cartesiano que original, só que usando uma cor diferente. Agora você já é capaz de comparar os gráficos e observar o comportamento dito acima.

Resolva alguns exercícios de funções inversas para treinar tudo o que aprendeu até aqui!

Gostou do nosso resumo de Função Inversa? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.

Experimente agora!