A Semelhança de triângulos é matéria que compara triângulos e seus elementos: se possuem ângulos correspondentes congruentes e lados correspondentes proporcionais. Se for o caso, é possível afirmar que esses triângulos são semelhantes, ou seja, possuem o mesmo formato ainda que tenham dimensões diferentes.
Neste artigo sobre Semelhança de triângulos você encontrará:
- O que é Semelhança de triângulos
- Constante e razão de proporcionalidade
- Casos da semelhança de triângulos
- Exemplo resolvido passo a passo
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
O que é Semelhança de triângulos?
Definição: Semelhança de Triângulos é a área da geometria que compara polígonos, no caso, os triângulos e seus elementos: lados e ângulos.
Quando comparamos duas figuras, é fácil tirar conclusões: algumas vezes são iguais (congruentes), outras são parecidas (semelhantes) ou ainda completamente distintas (diferentes). Se elas são iguais é como se fossem réplicas; se elas são distintas, não há nada em comum.
- Mas, quando são semelhantes, significa dizer que existe proporcionalidade entre lados e ângulos; ou seja, é como se você pegasse uma figura e a ampliasse, assim, todos os elementos aumentaram na mesma proporção.
Afinal de contas, como descobrir essa proporção?
Antes, vamos relembrar o conceito de correspondente congruente. Ser correspondente significa ocupar um lugar análogo, e congruente significa ser de valor parecido. Para entender melhor, veja o exemplo:
Julia, Marina e Bianca fizeram uma roda e Marina ficou à direita de Julia. Depois, Julia, Paula e Fernanda fizeram outra roda e Paula ficou à direita de Julia.
Observe que foram formadas 2 rodas diferentes, mas que a posição de Marina e de Paula são correspondes congruentes, pois ambas ocuparam lugares à direita de Julia.
Constante (k) e razão de proporcionalidade
Você se lembra do conceito de escala? É uma boa forma de entender o que é constante de proporcionalidade! Vamos trabalhar essa ideia antes de aplicá-la no triângulo! Veja:
Entendendo a ideia de razão e proporcionalidade
Uma parede mede 10m na vida real e está representada na maquete com 1m. Já a árvore mede 2m na vida real e está na maquete com 0,2m.
Se compararmos a relação que existe entre a árvore e a parede, ela será a mesma, seja na maquete ou na vida real:
- 10m (parede real) / 2m (árvore real) = 5 , ou seja, a árvore é 5x menor que a parede.
- 1m (parede maquete) / 0,2m (árvore maquete) = 5 , ou seja, a árvore permanece 5x menor que a parede.
Isso ocorre porque mesmo sendo representadas em outra escala (real ou maquete) a razão de proporcionalidade permaneceu a mesma:
- 10m (parede real) / 1m (parede maquete) = 10
- 2m (árvore real) / 0,2m (árvore maquete) = 10.
Constante em triângulos semelhantes
Por esse motivo, 2 triângulos só serão semelhantes se todas as divisões de lados correspondentes resultarem na mesma constante e tiverem ângulos congruentes.
Exemplo
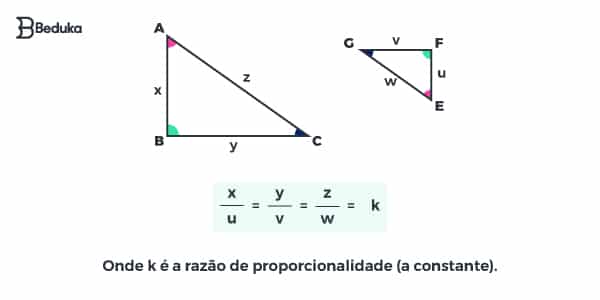
- Observe que o lado “x” ficou sobre o lado “u” porque ambos estavam entre ângulos correspondentes congruentes (vermelhos e verdes), garantindo que são lados correspondentes.
Quais são os 3 casos de Semelhança de Triângulos?
A semelhança entre polígonos é observada seguindo os mesmos critérios, seja em pentágonos ou retângulos. Porém, os triângulos possuem a estrutura mais simples, então é possível verificar a semelhança só com “macetes”. Basta observar se eles se enquadram em um dos casos: Ângulo-Ângulo, Lado-Lado-Lado ou Lado-Ângulo-Lado.
1- Caso Ângulo Ângulo (AA)
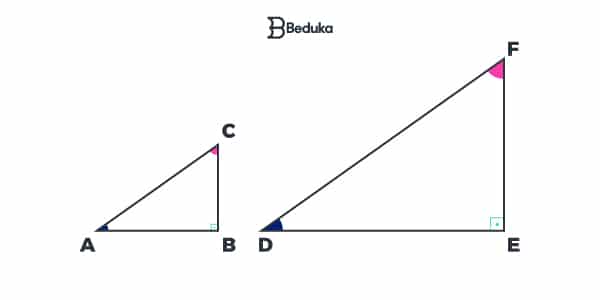
Dois triângulos são semelhantes se possuírem dois ângulos correspondentes congruentes.
Não é necessário verificar o terceiro ângulo e nenhuma proporcionalidade entre os lados, pois o triângulo só pode ser formado com 3 ângulos e o último segue o encaixe que restar dos outros 2.
Se eu quero fazer um triângulo com ângulos de 30° e 60°, com certeza o último deve valer 90° (regra da soma dos ângulos internos de um triângulo).
Quanto ao valor dos lados: se 2 ângulos já são correspondentes congruentes e os lados não fossem correspondentes proporcionais, o triângulo “não fecharia”. Você poderia até ajeitar para que os lados fechassem, mas alteraria os ângulos!
Atenção:
Não saia por aí acreditando que todos os pares de triângulos com 2 ângulos iguais são semelhantes! É necessário que também sejam ângulos correspondentes!
2- Caso Lado Lado Lado (LLL)
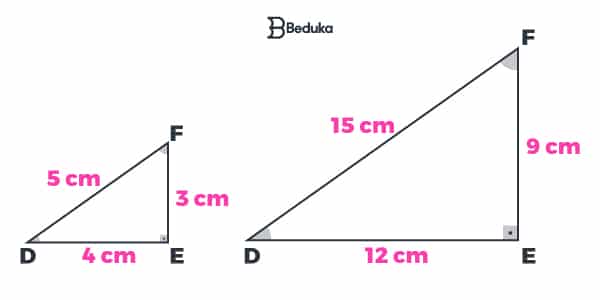
Se dois triângulos possuem três lados correspondentes proporcionais, então são semelhantes.
Não é necessário verificar os ângulos caso você tenha certeza dos 3 lados, pelo mesmo motivo do “encaixe” explicado no item acima!
3- Caso Lado Ângulo Lado (LAL)
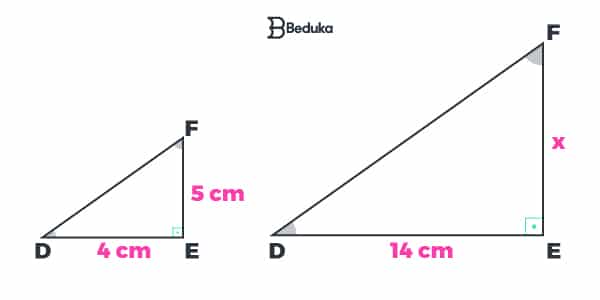
Dois triângulos que possuem dois lados correspondentes proporcionais e o ângulo entre eles congruente são semelhantes. Observe este caso de semelhança no exemplo:
- Se quisermos descobrir quanto deve valer “x” para que os triângulos sejam semelhantes, basta recorrer ao caso LAL e aplicar a ideia de razão de proporcionalidade:
14 / 4 = 3,5
logo
x / 5 = 3,5
x = 3,5 . 5
x = 17,5
Triângulo interceptado por uma reta paralela
Uma figura muito comum de aparecer em provas é o triângulo interceptado por uma reta paralela a um de seus lados! Justamente porque essa reta causa o surgimento de um outro triângulo menor e interno, que é semelhante ao seu originário.
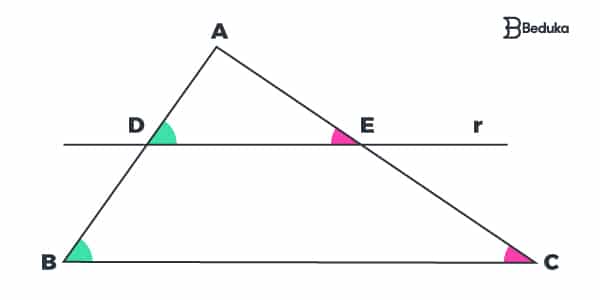
Confira para não ser pego de surpresa na prova: representação do triângulo “ABC“ e da reta “r”, que é paralela ao lado “BC”.
Observando a figura, notamos que os ângulos “B” e “D” são correspondentes congruentes , bem como os ângulos “C” e “E”.
Assim, pelo caso AA, os triângulos ABC e ADE são semelhantes.
Além disso, essa figura também lembra o formato do que chamamos de Teorema de Tales, e que garante a proporcionalidade!
Gostou do nosso artigo sobre Semelhança de triângulos? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





