Visão espacial matemática é a habilidade de identificar, situar e posicionar corpos no local. Ela é um dos mecanismos básicos da Geometria Espacial que estuda aquelas figuras com três dimensões: altura, largura e comprimento. Assim, entender as propriedades dos sólidos geométricos e dos corpos redondos é um dos objetivos da visão espacial!
Neste artigo sobre Visão espacial matemática, você encontrará:
- O que é visão espacial matemática?
- Figuras espaciais e planas – sólidos geométricos
- O que é Geometria espacial? Exemplos
- Como melhorar a visão espacial? Geometria espacial no cotidiano
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
O que é visão espacial matemática?
A visão ou percepção espacial é a habilidade de se situar, mover e identificar representações do que acontece ao nosso redor. Além disso, é saber posicionar e analisar os corpos (animados ou inanimados) no espaço.
Confuso? Calma. Vamos ao exemplos práticos:
Quando você desenha um círculo e pedimos que coloque um coração no centro, você está treinando as habilidades de ver, mover, identificar e situar. Além disso, sabe o que significa os conceitos de “centro” e “círculo”.
Porém, o círculo é um elemento da Geometria Plana, ele só possui duas dimensões: altura e largura.Tanto é que podemos desenhá-lo no plano cartesiano de eixos x e y.
Quando pedimos que você posicione um objeto no centro de uma esfera, as coisas ficam um pouco diferentes. Se você olhar para frente da esfera e colocar o objeto no meio de sua frente, estará incorreto. Essa seria a visão plana.
Como a esfera é um corpo redondo, um sólido geométrico, ela possui uma dimensão a mais que os planos: a profundidade. Por tanto, para posicionar algo son centro, é preciso ter a noção de que iremos “atravessá-la” e colocar dentro.
Ter essas percepções é o que chamamos de visão espacial.
Figuras espaciais e planas – sólidos geométricos
A Geometria Espacial é uma área da matemática que estuda as figuras no espaço, ou seja, aquelas que possuem três dimensões:
- Altura
- Largura
- Profundidade
A geometria espacial é a análise de sólidos geométricos, sejam corpos redondos (esfera, cone e cilindro) ou não (cubo, paralelepípedo, prisma e pirâmides). Eles são formados de arestas, vértices e faces.
Aqui colocamos apenas um brevíssimo resumo do que é geometria espacial, para você relembrar do que estamos falando e ter noção de como isso está ligado à visão espacial. Mas se quiser aprender mesmo sobre a Geometria Espacial, confira nosso artigo com exemplos e fórmulas!
Diferentemente, a Geometria Plana é o estudo de figuras bidimensionais, aquelas que possuem:
- Altura
- Largura
Suas figuras mais conhecidas são traçadas por meio de pontos e retas, sendo: círculo, quadrado, triângulo, retângulo, pentágono, hexágono, etc.
Como você deve ter notado, as figuras da plana só podemos pegar em mãos se estiver desenhado em uma folha. Já os da espacial, podemos tatear todos os lados.
Ambas podem ser representadas em um desenho, mas para retratar todos os lados da espacial, é preciso ter a visão que interprete essa tridimensionalidade e diferencie das figuras planas.
Observe as figuras a seguir e identifique suas diferenças:
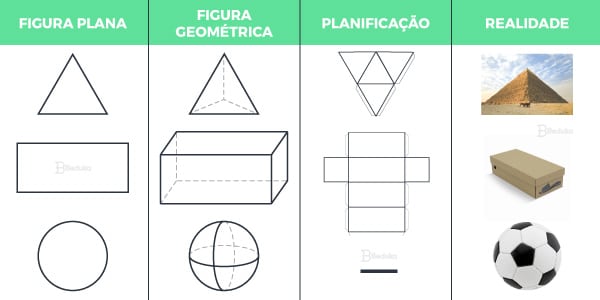
Importância da visão espacial matemática
É na primeira infância, o período que abrange até dois anos de idade, que a criança desenvolve a percepção sobre o espaço. Esse processo acontece por várias causas e influências, visto que a criança começa a focar nos seus sentidos e não só nos instintos.
Assim, as percepções do espaço tátil, auditivo, visual e oral; permitem à criança começar a andar e se locomover na vida real.
Então, dos dois aos sete anos a criança reconhece o que é um espaço e entende que isso é comum. Por isso, no Ensino Fundamental da escola nós montamos os sólidos geométricos, mas desde antes já brincávamos com bloquinhos!
Depois já introduzimos a Geometria plana e logo aparece a Espacial, juntamente com a Geometria Analítica. Nessa última, a representação de uma imagem (seja bi ou tri dimensional) é projetada e analisada como vetores: módulo (valor numérico positivo), direção (horizontal ou vertical) e sentido (para cima, para baixo, direita ou esquerda).
Assim, inserimos equações e cálculo para ter precisão daquilo que já conhecíamos pela visão espacial. Por isso, ela é a base essencial para toda a matemática que será desenvolvida a seguir.
Na escola, os conteúdos que precisam de uma boa visão espacial para serem desenvolvidos são:
- O plano e o espaço
- Volume do prisma, esfera, pirâmide
- Posições relativas ponto, reta e plano
- Projeções ortogonais, paralelas e transversais
- Área lateral e área total dos sólidos e corpos redondos
- Simetria e Proporção
Como melhorar a visão espacial? Geometria espacial no cotidiano

Você pode já ter entendido do que se trata e conseguido assimilar as figuras acima…Mas quando nos deparamos com alguma questão e não entendemos o desenho de primeira, bate logo aquele desespero!
Por isso, temos algumas dicas para te ajudar a ter uma boa visão espacial, desde as crianças até os adultos:
- Use os conceitos e vocabulário espacial.
A primeira forma de lembrar algo no dia a dia é saber os conceitos, nomear e tentar identificá-los nas coisas que vemos. Assim, vai criando uma familiaridade que facilita a memória!
- Jogue xadrez e quebra-cabeças.
Sim, eles são ótimos jogos para treinar o raciocínio lógico e a disposição das peças no espaço. Eles são a dupla mágica para te preparar para tudo na matemática!
- Brinque com Lego e Minecraft.
Essa dica pode ter feito você rir, mas é essencial para entender e tatear os sólidos geométricos e suas posições. Assim, o seu cérebro irá criar memórias dessas imagens e na hora da prova vai te ajudar a assimilar o desenho.
- Pilote um drone ou carrinhos de controle remoto
Mais uma coisa divertida e para todas as idades, esse desafio irá treinar a locomoção no espaço em todos os sentidos possíveis, além de ter a percepção de velocidade e curva.
- Crie maquetes e monte sólidos geométricos
Você deve se lembrar de ter feito isso quando era criança, mas refaça agora e prestando atenção em cada etapa. A planificação de sólidos é essencial para entender como eles se comportam.
Gostou do nosso artigo sobre Visão espacial matemática? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





