Os Cones são sólidos bastante famosos, eles estão muito presentes no nosso dia, como a casquinha de um sorvete ou um chapéu de aniversário, já reparou? Mas não basta saber só sobre eles; as provas sempre gostam de um desafio. Então é bom que você entenda também de Tronco de Cone, afinal, isso pode fazer toda a diferença no meio de uma questão!
Seja qual for sua dúvida, nós temos a resposta. Para te ajudar a ir direto ao ponto, você pode clicar em um dos tópicos abaixo:
- O que é um tronco de cone?
- Qual a diferença de cone e tronco de cone?
- Como um tronco de cone é formado?
- Quais são os elementos do tronco de cone?
- Como calcular a área de um tronco de cone? (total e lateral + geratriz)
- Qual o volume de um tronco de cone? (dois jeitos + curiosidade)
Faça um ótimo proveito do conteúdo e lembre-se de que é preciso treinar aquilo que aprendemos. E é por isso que nós temos um simulado Enem gratuito e online, que pode ser personalizado com as áreas que você quiser!
Agora vamos ao principal.
O que é um tronco de cone?
O tronco de cone é um sólido geométrico do tipo corpo redondo. Isso significa que ele é 3D (possui três dimensões e pode ser tateado em vários lados) e que possui algumas partes arredondadas.
Só que ele é um caso especial, porque está diretamente relacionado com os cones…
Qual a diferença de cone e tronco de cone?
Basicamente, a diferença entre cone e tronco de cone é que o primeiro é a figura original, já o segundo é uma derivação.
Em palavras mais simples, podemos dizer que o cone é a “mãe” e o tronco de cone é o “filho”, porque contém apenas uma parte do cone que o originou.
Tranquilo até aqui. Agora vamos entender matematicamente como uma coisa dessas pode acontecer!
Como um tronco de cone é formado?
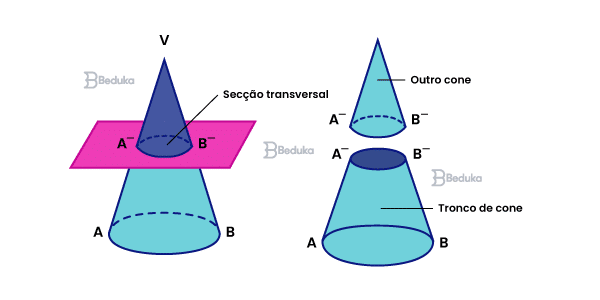
Pelo próprio nome desse sólido já fica bem óbvio que ele veio de um cone. Então o nosso conhecimento sobre essa figura precisa estar em dia se quisermos entender o que é um tronco.
Vou até te dar uma mãozinha: os cones têm uma ponta em cima e uma base circular embaixo, formando uma figura que vai afinando de baixo para cima.
Agora imagine que pegamos um cone e fizemos cortes.
A secção transversal é o nome que damos para dizer que pegamos um cone em pé e “passamos uma faca” no meio dele, cortando horizontalmente.
Dessa forma, nós vamos ter duas partes:
- A de cima, com a pontinha do cone (que será um mini-cone).
- A de baixo, sem pontas e com duas bases (que é o tronco de cone).
Explicando assim fica fácil de entender, não é? Agora que você já conhece os nomes, vamos resumir tudo isso em uma definição mais formal:
“O tronco de cone é um sólido obtido pela secção transversal de um plano (paralelo à base) no cone, independente da altura. Assim, o tronco formado corresponde à parte de baixo e sempre terá duas bases de mesmo formato e diferentes tamanhos.”
Viu como um corte muda tudo? Não é à toa que esse sólido tem fórmulas próprias de volume e área.
Ah, a informação no final dessa definição é nova. Então, antes de falarmos das fórmulas, vamos só dar uma olhada nos conceitos sobre as partes do tronco de cone.
Quais são os elementos do tronco de cone?
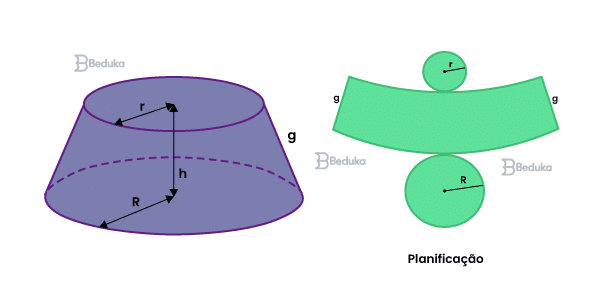
Alguns deles você já conheceu quando falamos aí em cima sobre a formação dos troncos de cone. Agora vamos só resumir as partes e as características mais importantes:
- Base maior (B): é a base original que restou do cone de origem, costuma ser a face inferior e sempre será circular.
- Base menor (b): é a face formada pela secção transversal, que costuma ficar em cima. Apesar de ser menor, também tem sempre o mesmo formato circular.
- Face lateral: o tronco de cone só tem uma, que é a parte arredondada.
- Aresta: o tronco de cone não possui aresta porque é corpo redondo. Ele possui geratriz!
- Geratriz (g): é o segmento de reta que passa pela face lateral (superfície do sólido) e liga as duas bases do tronco de cone.
- Vértice: não possui.
- Altura (h): é o segmento de reta vertical que liga a base menor à base maior, sempre formando um ângulo reto (90°).
- Raio menor (r): é o raio da base menor.
- Raio maior (R): é o raio da base maior.
Atenção: uma questão pode dar, em uma mesma imagem, o cone seccionado mostrando o tronco e o mini-cone da ponta. Cuidado para não confundir as medidas!
Normalmente, haverá traços no desenho indicando a qual parte cada número pertence. A altura do cone, por exemplo, costuma vir indicada por H, a do tronco de cone por h e a do mini-cone por h’.
Resumindo, podemos dizer que H = h + h`.
Como calcular a área de um tronco de cone?
Quando falamos em calcular a área de uma figura plana é simples, estamos falando do preenchimento daquela figura de 2 dimensões. Ou seja, o “colorido” dentro de um quadrado, por exemplo.
Só que a área de um sólido geométrico, que é tridimensional, não é o preenchimento da figura. Neste caso, seria o volume.
Afinal, o que seria então a área do tronco de cone? A área do tronco de cone será dada pela soma das áreas de todas as faces e bases!
Então precisamos calcular a área de cada parte e somá-las para dar a área total do tronco de cone. Se falarmos em área lateral, é só excluir as bases da operação.
Só que a conta dá menos trabalho do que você imagina:
- As bases têm sempre o mesmo formato circular, então você só precisa lembrar da fórmula de área do círculo.
- Já as faces laterais são calculadas usando o valor da geratriz.
- Por fim é só somar os valores se quiser a área total.
Traduzindo tudo isso para uma expressão, teremos:
At = AB + Ab + Al
Sendo que:
At = área total do tronco.
AB = área da base maior (que é a área de um círculo usando R).
Ab = área da base menor (que é a área de um círculo usando r).
Al = área lateral do cone.
E adivinhe só, antes de mostrar a área lateral do cone, precisamos entender como achar a geratriz!
Como calcular a geratriz de um cone?
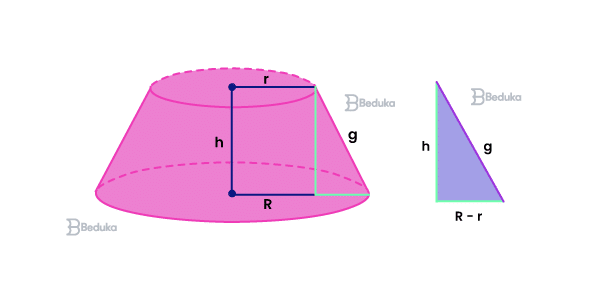
Pode parecer algo confuso à primeira vista, mas é simples: só precisamos usar o teorema de Pitágoras.
Observe a figura acima. O tronco de cone tem o formato de um pudim, então podemos tirar uma “fatia” dele Essa fatia pode ser feita de modo a formar um triângulo retângulo, onde a geratriz corresponde justamente à hipotenusa.
Aí é só fazer o cálculo da hipotenusa (geratriz) usando as medidas dos catetos. Um dos catetos será a altura do tronco e o outro será dado pela diferença entre os raios das bases.
E como calcular a área lateral de um cone?
Agora que você já viu a planificação do tronco de cone e como calcular a geratriz, fica fácil de calcular a área lateral. Ela será dada pela fórmula:
Al = πg (R + r)
Sendo que:
Al = área lateral do cone.
π = número pi, aproximadamente 3,14.
g = valor da geratriz.
R = raio da base maior.
r = raio da base menor.
Qual o volume de um tronco de cone?
O volume do tronco de cone é o preenchimento dele, como se fossemos encher um recipiente de água.
O jeito mais prático é calcular o volume do cone original e subtrair o volume do mini-cone formado acima do corte transversal. O restante corresponde justamente ao volume do tronco.
É com base nesse raciocínio que chegamos à expressão da fórmula:
Vt = VC – Vc
Sendo que:
Vt = volume do tronco
VC = volume do cone original
Vc = volume do cone menor
Ah, você não está lembrando da fórmula de volume do cone? Bem que eu te disse que precisávamos estar com esse assunto em dia para continuarmos neste artigo…
Curiosidade…
Sinceramente, eu acho difícil algum estudante decorar, mas existe sim uma fórmula prontinha para ser usada e que chegue no volume do tronco de cone.
É essa aqui:
Incrível né? Você pode escolher qual delas quer usar, mas o importante mesmo é entender o raciocínio que tem por trás. É isso que vai dar aquela luz no meio de uma questão.
Você achou que a explicação foi fácil de entender? Eu espero que tenha te ajudado, pois agora você já sabe tudo o que é essencial para acertar as questões de tronco de cone.
Se gostou do conteúdo e quer ficar por dentro das novidades do Beduka, você pode nos seguir no Instagram.
Faça bom proveito de todo esse conteúdo!





