A Função Exponencial é caracterizada pela presença da variável (x) no expoente de uma base numérica. Como toda função, há uma relação de dependência entre o valor de Y e esse expoente. Leia nosso resumo e coloque seu conhecimento em prática com nossa lista de Exercícios de Função Exponencial selecionada dos maiores vestibulares do Brasil.
Quando você terminar os Exercícios de Função Exponencial, faça nosso Simulado Enem. Coloque em prática todo o seu estudo, escolhendo as matérias que deseja treinar.
A Função Exponencial é a responsável por descrever a velocidade de crescimento exponencial de alguma coisa.
O que é crescer Exponencialmente?
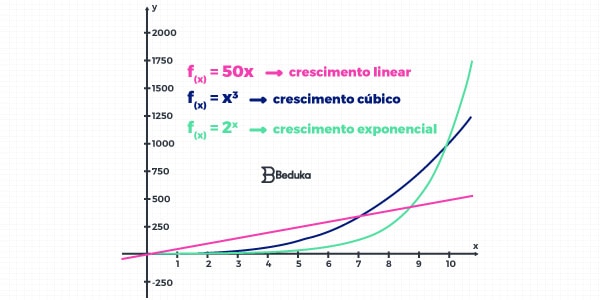
É crescer em função de alguma potência, de maneira que o número aumenta rapidamente com o tempo. Observe esta imagem:
Esse crescimento exponencial existe em vários setores da sociedade: nas Finanças, na Geografia, em áreas da Biologia (como o próprio cálculo do crescimento de pandemia) e etc…
A Função Exponencial é responsável por descrever a forma com que esse crescimento ocorre.
Pronto para entender mais a fundo sobre como funciona a Função Exponencial? Então vamos lá!
O que é Função Exponencial?
Uma Função Exponencial é caracterizada pela presença da variável (x) no expoente de uma base numérica. Como toda função, há uma relação de dependência entre o valor de Y e esse expoente.
Podemos escrever uma função exponencial qualquer usando a definição geral:
- f: R→R tal que y = aˣ, sendo que a > 0 e a ≠ 1
Para facilitar, confira exemplos numéricos de funções exponenciais:
- y = 2ˣ + 1
- y = 0,3ˣ
- y = 5ˣ
Classificamos uma função como exponencial quando a variável está no expoente e a base é sempre diferente de 1 e maior do que 0.
É preciso que haja essas restrições, pois qualquer número elevado a 1 é igual a ele mesmo e qualquer número elevado a 0 é 1. Assim a função seria constante e não exponencial.
- Aprimore seu conhecimento estudando Função Constante.
Como resolver uma Função Exponencial?
É preciso encontrar uma igualdade entre potências de mesma base para que isso possibilite igualar os expoentes.
3 passos para resolver uma Função Exponencial
1 – Iguale as bases, pois, se as potências de mesma base são iguais, os expoentes também são.
Ou seja:
2 – Pensando na equação 4ˣ = 16, precisamos igualar a base dos dois lados da equação, logo, eu posso substituir 16 por 4².
3 – Sendo assim, eu sei que 4ˣ = 4², se as potências são iguais e as bases também, logo o os expoentes são iguais.
Então X=2.
Mais exemplos:
- 3ˣ = 27, logo, 3ˣ = 3³, sendo X = 3;
- 5ˣ = 125, logo, 5ˣ = 5³, sendo X= 3;
- 7ˣ = 2401, logo, 7ˣ = 74, sendo X = 4.
Escolhemos neste último exemplo um número bem grande, para mostrar como essa regra ela se aplica às mais diversas situações.
- Muito simples, não? Acredite É Possível Aprender Matemática!
A Representação Gráfica da Função Exponencial
Para construir um gráfico é necessário pegar uma função qualquer e estipular valores na variável (X) para encontrar o valor da função.
Depois, é só colocar no plano cartesiano!
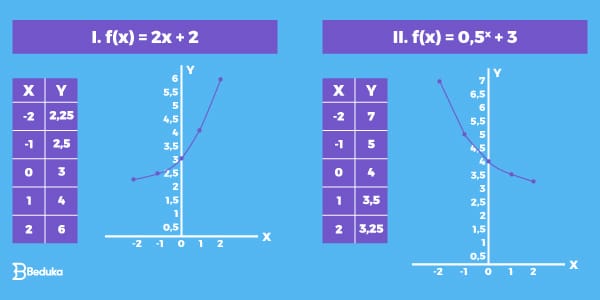
Exemplo: Vamos tomar as funções f(x) = 2ˣ + 2 e f(x) = 0,5ˣ + 3
Como o X é a variável e não há restrições, podemos atribuir qualquer valor a ele. As possibilidades são infinitas, mas procure usar valores pequenos para não complicar sua conta!
Usaremos os valores: -2,-1,0,1,2.
Depois de substituir, é fácil achar o valor de Y em função de X. Resolvemos as contas utilizando as propriedades da potenciação:
- Você lembra Quais são as Propriedades da Potenciação?


Com os pares ordenados em mãos, podemos construir os gráficos:
Com certeza você deve ter visto em algum momento na televisão a curva de contágio da COVID-19.
Bem, agora você compreende uma das bases matemáticas que está por trás dela.
Exercícios sobre Função Exponencial com Gabarito
No início até assusta, mas agora sei que com esse resumo tudo ficou mais claro para você. Que tal testar seu conhecimento com Exercícios de Função Exponencial.
Parabéns por ter lido até aqui!!!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Questão 1 – (Mack – SP) Dadas as funções f(x) = 2 x² – 4 e g(x) = 4 x² – 2x, se x satisfaz f(x) = g(x), então 2xé:
a) ¼
b) 1
c) 8
d) 4
e) ½
Questão 2 – (Unesp 2018) O ibuprofeno é uma medicação prescrita para dor e febre, com meia-vida de aproximadamente 2 horas. Isso significa que, por exemplo, depois de 2 horas da ingestão de 200 mg de ibuprofeno, permanecerão na corrente sanguínea do paciente apenas 100 mg da medicação. Após mais 2 horas (4 horas no total), apenas 50 mg permanecerão na corrente sanguínea e, assim, sucessivamente. Se um paciente recebe 800 mg de ibuprofeno a cada 6 horas, a quantidade dessa medicação que permanecerá na corrente sanguínea na 14ª hora após a ingestão da primeira dose será
a) 12,50 mg
b) 456,25 mg
c) 114,28 mg
d) 6,25 mg
e) 537,50 mg
Questão 3 – (UERJ 2013) Um lago usado para abastecer uma cidade foi contaminado após um acidente industrial, atingindo o nível de toxidez T0, correspondente a dez vezes o nível inicial.
Leia as informações a seguir:
- A vazão natural do lago permite que 50% de seu volume sejam renovados a cada dez dias.
- O nível de toxidez T(x), após x dias do acidente, pode ser calculado por meio da seguinte equação:
Considere D o menor número de dias de suspensão do abastecimento de água, necessário para que a toxidez retorne ao nível inicial.
Sendo log 2 = 0,3, o valor de D é igual a:
a) 30
b) 32
c) 34
d) 36
Questão 4 – (Unicamp 2014) O gráfico abaixo exibe a curva de potencial biótico q(t) para uma população de microrganismos, ao longo do tempo t.
Sendo a e b constantes reais, a função que pode representar esse potencial é
a) q(t) = at + b
b) q(t) = abt
c) q(t) = at2 + bt
d) q(t) = a + log b t
Questão 5 – (Enem 2015) O sindicato de trabalhadores de uma empresa sugere que o piso salarial da classe seja de R$ 1 800,00, propondo um aumento percentual fixo por cada ano dedicado ao trabalho. A expressão que corresponde à proposta salarial (s), em função do tempo de serviço (t), em anos, é s(t) = 1 800 . (1,03)t .
De acordo com a proposta do sindicato, o salário de um profissional dessa empresa com 2 anos de tempo de serviço será, em reais,
a) 7 416,00
b) 3 819,24
c) 3 709,62
d) 3 708,00
e) 1 909,62.
Questão 6 – (UEMA) Seja f(x) = 3x-4 + 3x-3 + 3x-2 + 3x-1. O valor de x para que se tenha f(x) = 40 é:
a) 0
b) -2
c) 1
d) 4
e) 3
Questão 7 – (PUC MG) Uma população de bactérias começa com 100 e dobra a cada três horas. Assim, o número n de bactérias após t horas é dado pela função. n(t) = 100 x 2t/3 Nessas condições, pode-se afirmar que a população será de 51.200 bactérias depois de:
a) 1 dia e 3 horas
b) 1 dia e 9 horas
c) 1 dia e 14 horas
d) 1 dia e 19 horas
Gabarito dos Exercícios de Função Exponencial
Exercício resolvido da questão 1 –
Alternativa correta: d) 4
Exercício resolvido da questão 2 –
Alternativa correta: b) 456,25 mg
Exercício resolvido da questão 3 –
Alternativa correta: c) 34
Exercício resolvido da questão 4 –
Alternativa correta: b) q(t) = abt
Exercício resolvido da questão 5 –
Alternativa correta: e) 1 909,62.
Exercício resolvido da questão 6 –
Alternativa correta: d) 4
Exercício resolvido da questão 7 –
Alternativa correta: a) 1 dia e 3 horas
Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos Exercícios de Função Exponencial? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.