Resumo de sistemas lineares: passo a passo com exemplos!

Ah, os sistemas… Muitos alunos tremem ao se deparar com várias equações de 3 ou mais incógnitas. Porém, agora você aprenderá a resolvê-los! Neste resumo de sistemas lineares, ensinamos os métodos de Cramer e do Escalonamento para você superar essa dificuldade. Tudo com exemplos e passo a passo!

Neste resumo de sistemas lineares, você encontrará os tópicos abaixo. Se quiser, clique em um deles para ir diretamente ao conteúdo:

1. Introdução: o que é uma equação?
2. O que são sistemas lineares?
3. Transformando sistemas em matrizes!
4. Como classificamos os sistemas?
5. Como resolvemos um sistema linear?
6. Como usar a Regra de Cramer? Exemplo em 3 passos!
7. Como resolver sistemas por Escalonamento? Exemplo em 3 passos!

Depois você pode testar o que aprendeu. É só fazer o nosso Simulado ENEM gratuito! Ele pode ser personalizado com as matérias que você quiser.

Introdução: o que é uma equação?

Antes de falar sobre sistemas de equações lineares, precisamos relembrar o que são as equações, seus tipos e propriedades. Relembre os conceitos básicos, que são importantíssimos para continuarmos:

• Equação é uma expressão algébrica

Isso significa que são formadas por letras e números, tendo um símbolo de igualdade (=) no meio. O lado esquerdo ao sinal é chamado de 1º membro e o lado direito é chamado de 2º membro.

• O nosso objetivo é achar quanto vale a incógnita

A incógnita é o valor desconhecido que representamos por letras, normalmente o x. Depois de descobrir esse valor, ao colocarmos um número no lugar do x, o resultado da equação precisa ser zero. Isso porque os dois membros devem ter o mesmo valor (é uma igualdade).

• Equações lineares são aquelas em que o maior expoente da incógnita é 1.

Isso significa que estamos falando de equações do primeiro grau. Além disso, nem sempre o segundo membro vem com algo escrito, ele pode aparecer como “0” se tivermos passado todos os seus elementos para o primeiro membro.

• A fórmula ax + b = 0 é a base para a equação do 1° grau com 1 incógnita.

Nela, o “a” é o coeficiente (número ≠ de 0) e o “b” é um termo independente (outro número, que pode valer 0). 

Exemplo: 3x + 5 = 0

• A fórmula ax + by + c = 0 é a base para a equação de 1° grau com 2 incógnitas. 

Nela, “a” e “b” são coeficientes (número ≠ 0) e “c” é o termo independente (outro número, pode valer 0). 

Exemplo: 2x + 3y – 6 = 0

• A fórmula ax + by + cz + d = 0 é a base para a equação de 1° grau com 3 incógnitas. 

Nela, “a”, “b” e “c” são coeficientes (número ≠ 0) e “d” é o termo independente (outro número, pode valer 0). 

Exemplo: 2x + 3y + 4z = 0

• Qualquer equação de primeiro grau pode ser escrita de forma genérica como:

a₁x₁ + a₂x₂ + a₃x₃… + a_nx_n = 0

São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!

Para que os sistemas lineares são usados?

O uso de sistemas lineares é cobrado nos vestibulares. Então para você, estudante, ele é essencial! 

Mas não é só isso…

Na prática, eles são usados nas ciências e na engenharia, como na eletrodinâmica, eletrônica, estática, aerodinâmica, entre outras. Ou seja, eles estão mais presentes no nosso dia a dia do que imaginamos, desde pegar um avião até entrar em um edifício!

Conceito: o que são sistemas lineares?

O sistema linear é o conjunto de duas ou mais equações de primeiro grau, podendo ter uma ou mais incógnitas. Como existem muitas possibilidades, cada sistema é identificado pelas equações que o compõem.

No sistema, as equações são representadas uma acima da outra, com uma chave do lado esquerdo. Esse é o símbolo usado para sinalizar que elas fazem parte de um mesmo grupo. 

Sendo assim, um sistema de “m” equações lineares e “n” incógnitas pode ser representado como sistema linear m × n. É importante lembrar que ele possui “m” equações onde cada equação deve conter as mesmas “n” incógnitas.

• Isso te lembrou algo? Se sim, você está certo: 

Essa também é a maneira com que representamos as matrizes. Portanto, é possível traduzir as informações do sistema para uma matriz e, a partir disso, extrair informações importantes sobre suas equações.

Saiba como:

Como transformar sistemas lineares em matrizes?

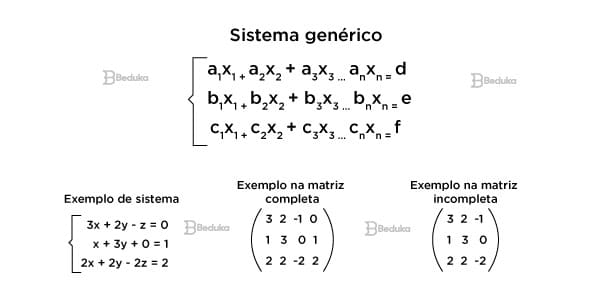
Para transformar sistemas lineares em matrizes, basta escrever os elementos da equação; só que ocultando as incógnitas e estando na ordem de cada elemento a_ij de uma matriz m x n. Repare na imagem acima para ver o exemplo.

Observe também que há duas formas de representarmos:

• Matriz completa: formada pelos coeficientes do sistema e seus termos independentes.
• Matriz incompleta: formada apenas pelos coeficientes do sistema.

Como você sabe, toda boa matriz vem acompanhada de um cálculo próprio, o Determinante. Ele é a ferramenta que aplicamos para extrair as informações preciosas.

Neste caso, o valor do Determinante nos permitirá classificar os sistemas lineares.

Acompanhe:

Como classificamos os sistemas lineares?

Dependendo da quantidade de soluções possíveis, cada sistema linear recebe uma classificação:

• Sistema Possível e Determinado (SPD): há uma única solução e ocorre quando o determinante for diferente de zero (D≠0).
• Sistema Possível e Indeterminado (SPI): as soluções são infinitas e ocorre quando o determinante for igual a zero (D=0).
• Sistema Impossível (SI): não há qualquer tipo de solução e ocorre quando o determinante principal for igual a zero e o determinante secundário for diferente de zero.

Além dessa classificação por resultado, podemos dar outras características aos sistemas.

Eles serão “homogêneos” quando o termo independente for igual a 0 (zero). Assim, aqueles que apresentarem um valor numérico no termo independente, serão chamados de “não-homogêneos”.

Eles ainda podem ser chamados de “normais” quando o número de equações é o mesmo que o número de incógnitas.

Como resolvemos os sistemas lineares?

Na verdade, há diferentes métodos dependendo do tipo de equação com que estamos lidando…

Quando o sistema linear possui equações com 2 incógnitas, os métodos mais práticos de resolução são a adição e a substituição.

Porém, quando falamos em sistemas de 3 ou mais incógnitas, aí precisamos de recursos novos: a Regra de Cramer e o Escalonamento.

Como resolver um sistema linear pela Regra de Cramer?

A Regra de Cramer é utilizada na resolução de sistemas SPD (sistemas possíveis e determinados). Ela consiste em fazer basicamente três etapas:

• 1° Passo: Calcular o determinante principal (D).
• 2° Passo: Calcular o determinante secundário (D_x, D_y, D_z).
• 3° Passo: Substituir na fórmula: x = D_x/D ou y = D_y/D ou z = D_z/D.

Lembrando que:

D → determinante da matriz incompleta do sistema.

D_x → determinante da matriz incompleta do sistema, substituindo a coluna de x pela coluna dos termos independentes.

D_y → determinante da matriz incompleta do sistema, substituindo a coluna de y pela coluna dos termos independentes.

D_z → determinante da matriz incompleta do sistema, substituindo a coluna de z pela coluna dos termos independentes.

Observe o exemplo a seguir:

Como resolver um sistema linear por Escalonamento?

O Escalonamento é um método onde utilizamos somente a matriz completa para realizar  operações entre as linhas.

Essa é uma forma de resolver o sistema transformando-o em outro sistema equivalente e mais fácil.

O objetivo é isolar as suas incógnitas e conseguir, assim, anular algumas delas para encontrar o seu valor.

• 1º passo: escrever a matriz completa que representa o sistema.
• 2° Passo: realizar operações entre as equações, para tentar eliminar ou simplificar alguma incógnita (somar ou subtrair uma equação pela outra / Multiplicar ou dividir uma das equações por um número / Trocar duas equações de posições).
• 3° Passo: reescrever o sistema a partir dos coeficientes simplificados na nova matriz e resolver normalmente.

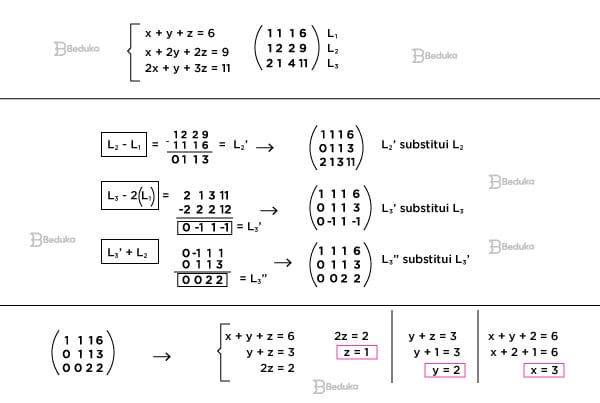
Observe o exemplo a seguir:

Gostou do nosso resumo de sistemas lineares? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.

Experimente agora!