O que é Arranjo: Tipos, suas fórmulas e exemplos!

O Arranjo (A n,p) é um tipo de agrupamento da análise combinatória formado por “p” elementos de um conjunto inicial “n”. Nesse caso, a ordem das combinações importa porque pode gerar resultados diferentes. Há 3 tipos de Arranjos, mas todos eles levam em conta a ordem e a natureza dos agrupamentos.

Ficou confuso? 

Calma, nós vamos te explicar desde o início! Neste texto sobre Arranjo, você encontrará os tópicos abaixo, suas explicações detalhadas e exemplos. Clique em um deles para ir diretamente ao conteúdo:

1. Introdução à Análise Combinatória.
2. O que é Arranjo?
3. Características dos Arranjos.
4. Símbolo dos Arranjos.
5. Fórmulas do Arranjo Simples e Repetição.
6. Tipos de Arranjo e quando usá-los.
7. Arranjo Simples + Exemplo de questão resolvida.
8. Arranjo com Repetição + Exemplo de questão resolvida.
9. Arranjo Condicional + Exemplo de questão resolvida.
10. Diferença entre Permutação, Arranjo e Combinação

• Estudando para as provas? Conheça O melhor Simulado do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!

Introdução à Análise Combinatória

A Análise Combinatória é a área da Matemática que estuda as formas de resolver problemas com contagem de elementos ou possibilidades de algo ocorrer. Ela vai nos dizer quais as técnicas e métodos para cada tipo de situação. 

O Princípio Fundamental da Contagem (PFC) e o Fatorial são contas que aprendemos a fazer desde o Ensino Fundamental, pois eles são a base da análise combinatória e seu raciocínio. Não deixe de ler antes de continuar!

Em outras situações, os cálculos tendem a se tornar complexos. Para facilitar o desenvolvimento das ideias, nós dividimos as técnicas de acordo com as situações. Elas podem ser um caso de Permutação, Arranjo ou Combinação.

O que é Arranjo?

O Arranjo é a quantidade de grupos que podemos fazer com “p” elementos retirados de um conjunto de “n” elementos. 

Quando escolhemos alguns elementos de um conjunto, podemos organizá-los de diferentes formas. Neste caso, a ordem com que organizamos e as trocas de suas posições fazem com que tenhamos resultados diferentes.

Exemplo

Vamos tomar como base um conjunto “n” formado por 4 elementos (1, 2, 3 e 4). Se nós queremos agrupar esses elementos de 3 em 3, teremos um arranjo p com 24 resultados: 

123, 124, 132, 134, 142, 143, 213, 214, 231, 234, 241, 243, 312, 314, 321, 324, 341, 342, 412, 413, 421, 423, 431 e 432. 

Cada um desses números é um arranjo diferente dos 4 elementos do conjunto, em grupos de 3 elementos. 

Características

Outra característica importante é notar que os Arranjos levam em conta a ordem e a natureza dos elementos. Vamos explicar:

Olhando os números acima, você percebe que todos os arranjos têm os mesmos elementos (1, 2, 3 e 4), mas formam números diferentes. Isso acontece por causa da ordem em que estão colocados, ou seja, a ordem importa.

Você também é capaz de perceber que, se estivéssemos arranjando os mesmos elementos desse conjunto em grupos de 2 em 2, nós teríamos uma quantidade diferente no resultado de arranjos. 

Portanto:

• Se compararmos os arranjos 342 e 324, perceberemos que eles são diferentes pela ordem dos seus elementos.
• Se compararmos os arranjos 342 e 341, perceberemos que eles são diferentes pela natureza de seus elementos.

Símbolo do Arranjo

O símbolo que representa a definição de Arranjo é:

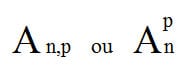
Lemos assim: “Arranjo de n elementos, de p em p.”

Em que:

• n = número de elementos do conjunto inicial.
• p = número de algarismo que os agrupamento deverão ser feitos.
• A = quantidade de arranjos possíveis dentro dessas condições.

Isso é válido desde que n ≥ p, pois é impossível eu querer arranjar 3 números em grupos de 4 algarismos, por exemplo.

Dessa forma, representamos o exemplo do primeiro tópico como A 4,3 = 24.

• São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!

Como calcular Arranjo Simples e com Repetição? (Fórmula)

Você viu no exemplo do tópico anterior que é muito trabalhoso ficar montando arranjos manualmente. Imagina se a questão pedisse um A 40,3… Além de dar trabalho e podermos nos confundir, quanto mais elementos maior o tempo gasto.

Pensando justamente nas questões de vestibulares, há uma fórmula que serve para calcular os Arranjos. Basta substituir cada elemento na posição correta e resolver como equação normal. Ela nos poupa tempo e trabalho!

Assim, não é necessário gastar tempo montando todos os arranjos possíveis, basta aplicar a fórmula: A n,p = n! / (n – p)!

• No próximo tópico, explicaremos a outra fórmula e os tipos de arranjos.

• Lembre-se: a exclamação (!) na frente do número remete à operação de Fatorial.

Tipos de Arranjos e quando usá-los

Nós sempre usaremos o Arranjo quando a questão der importância à ordem e à natureza. Ainda assim, existem várias situações diferentes que esses 2 fatores aparecem. É daí que surgem os 3 diferentes tipos de Arranjo: Simples, com Repetição e Condicional.

Vamos conhecê-los!

Arranjo Simples

O arranjo será simples sempre que não houver um elemento repetido no conjunto inicial. Nessa situação, cada elemento só pode ser usado uma vez.

Exemplo

Uma turma do Ensino Fundamental tem 15 alunos e a professora pediu que eles se juntassem em duplas para criar uma chapa com representante e vice-representante. Quantas são as possibilidade totais de chapas?

Solução

Se estamos falando em representante e vice-representante, a ordem dos alunos importa. Afinal, ter João como representante e Maria como vice é diferente de ter Maria como representante e João como vice.

Além disso, sabemos que não haverá repetições, pois cada pessoa é única. Com base nessa análise, sabemos que se trata de um A 15,2.

Agora, basta substituir na fórmula e resolver: 

A 15,2 = 15! / (15 – 2)!

A 15,2 = 15! / 13!

A 15,2 = 15.14.13! / 13!

A 15,2 = 15.14

A 15,2 = 210

Arranjo com Repetição

Os arranjos com repetição são aqueles em que se aceitam elementos repetidos. Por isso, cada posição poderá ser preenchida por qualquer um de todos os elementos do conjunto inicial. 

Perceba que nós estaremos multiplicando o “n” por ele mesmo na quantidade de “p” que for pedido. Então a fórmula a ser usada é:

Acr n,p = n^p

Exemplo

José quer formar uma senha de 6 dígitos para sua conta no banco e ela só pode ser feita com os números de 0 a 8. Quantas são as possibilidades de senha que ele tem?

Solução

Se estamos falando em senha e números, com certeza a ordem importa e usaremos arranjo. Além disso, não foi mencionado nada sobre proibir repetição, então se trata de um arranjo com possibilidade de repetição.

Se José só pode usar números de 0 a 8, então temos 9 elementos disponíveis no conjunto inicial (n). Além disso, a senha deve conter 6 dígitos, então os agruparemos de 6 em 6. Isso nos dá um Ar 9,6.

Então a fórmula a ser usada é:

Acr 9,6 = 9⁶

Acr 9,6 = 531 441

Arranjo Condicional

Este tipo de arranjo é marcado por alguma condição extra que foi dada naquele exemplo. precisamos avaliar caso a caso para ver quais métodos iremos usar.

Exemplo

Quantos arranjos com quatro elementos do conjunto {I, J, K, L, M, N}.  começam com duas letras do subconjunto {L, M, N}?

Solução

Observe que nessa situação as duas primeiras letras tem uma condição específica, por isso, vamos separar o raciocínio em dois momentos: selecionamos as duas primeiras letras e depois as possibilidades para as últimas.

A escolha das duas primeiras letras precisa ser parte do conjunto {L, M, N}, então se trata de um arranjo simples de 3 elementos 2 a 2, ou seja, A 3,2.

Se foi pedido um arranjo total de 4 letras, então falta escolher as duas últimas letras. Isso deve ser feito pelo arranjo das letras {I, J, K, L, M, N}. 

Porém, devemos retirar as duas que já foram escolhidas. Então será um arranjo simples de 4 elementos 2 a 2 (A 4,2), não um arranjo de 6 elementos 2 a 2.

Pelo princípio multiplicativo, podemos dizer que a resposta final será encontrada por A3,2 x A4,2.

Vamos resolver as contas separadamente para não confundir e depois multiplicar seus resultados.

• A 3,2 = 3! / (3-2)!

A 3,2 = 3! / 1!

A 3,2 = 6

• A 4,2 = 4! / (4-2)!

A 4,2 = 4! / 2!

A 4,2 = 12

• Então A3,2 x A4,2 = 

6 x 12 = 

72

Diferença entre Permutação, Arranjo e Combinação

Nós te dissemos que a análise combinatória é a área que estuda diferentes métodos para diferentes casos, sendo eles: Arranjo, Permutação e Combinação.

A essa altura, você já entendeu o que são Arranjos: ordem e natureza importam.

Resumidamente, as Combinações são agrupamentos em que não importa a ordem (só importa a natureza). Imagine a professora escolhendo uma dupla para bater corda. Não faz diferença se ela disser “João e Maria” ou “Maria e João”, ambos irão participar. 

Já a Permutação é um caso específico de Arranjo. Nela, só a  ordem importa (a natureza não), porque o número de elementos do conjunto é igual ao número de elementos agrupados, ou seja, n = p.

Gostou do nosso artigo sobre Arranjo? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.

Experimente agora!