A análise combinatória é a parte da Matemática responsável por estudar métodos e técnicas que resolvem problemas relacionados à contagem. Ela faz análise das possibilidades e combinações possíveis entre um conjunto de elementos, e é muito utilizada nos estudos sobre probabilidade.
Aprenda um pouco mais de matemática com esse Resumo de Análise Combinatória que o Beduka preparou para te ajudar a se preparar para o ENEM e outros vestibulares.
Não deixe de conferir nossos exercícios sobre Análise Combinatória.
Nesse artigo vamos falar sobre:
- Resumo de Análise Combinatória;
- Princípio fundamental da contagem;
- Fatorial, arranjo, permutação e combinação;
O que é Análise Combinatória?
Para começar a fazer um resumo de análise combinatória, precisamos entender primeiro o que ela significa.
A análise combinatória pode ser definida como sendo um conjunto de técnicas e métodos que estudam as combinações e possibilidades das variáveis de um conjunto. Constituído por elementos finitos, a análise combinatória se baseia em parâmetros que possibilitam a contagem.
Entender o que é análise combinatória é fundamental para quem deseja se sair bem na prova do ENEM ou em outro vestibular, pois esse tema é bastante frequente nas provas de Matemática. Além de envolver cálculos matemáticos, a análise combinatória também abrange fatores lógicos.
A análise combinatória se resume em 6 procedimentos principais:
- Fatorial;
- Princípio fundamental da contagem;
- Arranjos simples;
- Permutação simples;
- Combinação;
- Permutação com elementos repetidos.
1. Fatorial
Considerando n um número natural maior que 1, o fatorial desse número n, que é representado por n!, pode ser definido como:
n! = n(n – 1) x (n – 2) x (n – 3)x…x 3 x 2 x 1
Lê-se n! como: n fatorial ou fatorial de n.
Não deixe de conferir nossos exercícios sobre fatorial com gabarito!
2. Princípio Fundamental da Contagem
De acordo com o princípio fundamental da contagem, se um evento é composto por duas ou mais etapas sucessivas e independentes, o número de combinações será determinado pelo produto entre as possibilidades de cada conjunto.
Exemplo:
Numa pizzaria há 8 tipos de sabores, 5 tipos de sucos e 6 tipos de sobremesas. Quantas são as possíveis combinações de um lanche nessa pizzaria?
Utilizando o princípio fundamental da contagem temos:
8 x 5 x 6 = 240 maneiras de se fazer um lanche.
3. Arranjos Simples
O arranjo simples é o agrupamento dos elementos de um conjunto que dependem da ordem e da natureza dos mesmos.
Para obter o arranjo simples de p elementos de um conjunto total n, onde p ≤ n, utiliza-se a seguinte expressão:
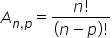
An,p = Arranjo de p elementos de um total n
n = elementos totais do espaço amostral
p= números de elementos no arranjo
Exemplo:
Considere uma votação para escolher um representante e um vice-representante de uma turma, com 20 alunos. O mais votado será o representante e o segundo mais votado o vice-representante. Dessa maneira, de quantas maneiras distintas a escolha poderá ser feita? Nesse caso a ordem é importante, visto que altera o resultado final.
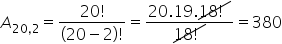
Logo, o arranjo pode ser feito de 380 maneiras diferentes.
4. Permutações Simples
A permutação simples pode ser considerada como um caso particular de arranjo, onde os elementos irão formar agrupamentos que se diferenciam somente pela ordem. As permutações simples dos elementos P, Q e R são: PQR, PRQ, QPR, QRP, RPQ, RQP.
Se chamarmos de Pn a permutação simples de n elementos distintos, podemos calculá-la através da seguinte fórmula:
Pn = n!
Onde n! = n x (n-1) x (n-2) x (n-3) x…..x 3 x 2 x 1
Exemplo: 4! = 4 x 3 x 2 x 1 = 24
5. Combinações Simples
As combinações são agrupamentos em que a ordem dos elementos não é importante, mas são caracterizadas pela natureza dos mesmos. Assim, para calcular uma combinação simples de n elementos tomados p a p (p ≤ n), utiliza-se a seguinte fórmula:
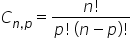
Cn,p = Combinação de p elementos de um total n
n = elementos totais do espaço amostral
p= números de elementos no arranjo
Exemplo
Considerando a escolha de 3 membros para formar uma comissão de formatura, dentre 10 pessoas que se candidataram para fazer parte. De quantas maneiras distintas essa comissão poderá ser formada? Note que, ao contrário dos arranjos, nas combinações a ordem dos elementos não é relevante. Isso quer dizer que escolher Guilherme, Rafael e Juliana é equivalente à escolher Juliana, Rafael e Guilherme.
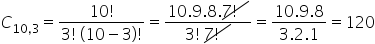
Para simplificar os cálculos, transforma-se o fatorial de 10 em produto, mas conserva-se o fatorial de 7, pois assim é possível simplificar com o fatorial de 7 do denominador.
Desta forma, existem 120 maneiras distintas de formar a comissão.
Confira também nossos exercícios de probabilidade.
6. Permutação de elementos repetidos
Permutação de elementos repetidos deve seguir uma forma diferente da permutação, pois elementos repetidos permutam entre si.
A fórmula da permutação simples de n elementos diferentes é representada por Pn. Logo, tomemos como exemplo a palavra CATRACA, que tem 7 elementos:
Pn = n!
P8 = 7! = 5040
Entretanto, a palavra CATRACA possui elementos repetidos, uma vez que a letra A se repete por três vezes e a letra C repete 2 vezes. Neste caso, outra fórmula é utilizada:
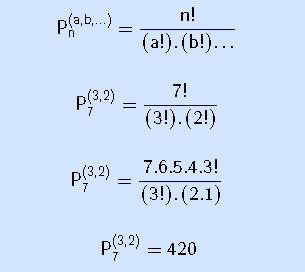
Você acabou de conferir um Resumo de Análise Combinatória. Estude para o ENEM e outros vestibulares com outro resumo de conjuntos numéricos. Você também pode testar os seus conhecimentos sobre diversas matérias no nosso Simulado ENEM. É gratuito!
Gostou do Resumo de Análise Combinatória? Queremos te ajudar também a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!








2 Comentários
Excelente trabalho é realizado pelo Pinterest Eu acho fantástico.
??????