Fatoração é o nome do processo matemático usado para decompor um número em algarismos primos ou para simplificar expressões polinomiais. Isso é feito quando os representamos usando produtos de fatores, ou seja, multiplicações. Ainda é possível determinar o MDC e o MMC usando essa operação!
Neste artigo sobre Fatoração, você encontrará:
- O que é Fatoração
- O que são números primos e polinômios
- Para que serve a Fatoração
- Como fazer fatoração completa
- Tipos de Fatoração (fator comum, agrupamento, cubos e quadrados perfeitos, etc.)
- Como achar MDC e MMC usando Fatoração
- Estudando para as provas? Conheça O melhor Simulado Enem do Brasil! Ele pode ser personalizado com as matérias que você mais precisa! É gratuito e online!
O que é Fatoração?
Fatoração é o nome do processo matemático que usamos para decompor um número ou expressão. Isso é feito quando os representamos por meio de produtos de fatores (multiplicações).
A ideia de fatoração surge a partir do teorema fundamental da aritmética, uma afirmação que diz:
“Qualquer número inteiro maior que 1 pode ser escrito na forma de produtos de números primos”
Lembre-se: números primos são aqueles que só se dividem por eles mesmos e por 1, eles não tem outros divisores. Compare o número 6 e o número 13:
- 6 é divisível por 1, 2, 3 e 6.
- 13 só é divisível por 1 e 13, portanto, é primo.
Isso tudo quer dizer que podemos representar o número 12, por exemplo, em uma forma decomposta que só envolve a multiplicação dos menores números primos. Se fizermos a fatoração do 12, teremos o resultado “2 x 2 x 3”.
Para que serve a Fatoração?
Você deve estar se perguntando qual é o sentido de pegar um número e representá-lo na forma de várias multiplicações. Pois é, por incrível que pareça, ela é uma grande aliada!
- A fatoração é muito importante quando estamos lidando com radiciação ou equações irracionais, pois é por meio dela que conseguimos “tirar a raiz” de certos números.
- Ela também pode ser uma ferramenta muito útil para identificar o Máximo Divisor Comum (MDC) e o Mínimo Múltiplo Comum (MMC) de um número.
- A fatoração de polinômios é o que nos permite simplificar as expressões algébricas para conseguirmos resolvê-las. Você deve se lembrar que usamos muito a simplificação de polinômios na Geometria Analítica e na Física.
Em outras palavras, usamos a fatoração de expressões para converter os polinômios que possuem somas e subtrações (difícil fazer operações) em uma equação com fatores multiplicativos (fácil de fazer operações).
Você esqueceu o que são polinômios? Vamos te explicar:
“Números” são os algarismos puros, que não apresentam letras. Exemplo: 24, 13 e 456.
“Monômios” são expressões que misturam números com 1 letra. Exemplo: 2x e 5y.
“Polinômios” são expressões algébricas com duas ou mais letras. Exemplo: 2x+4y.
Agora, nós vamos sair da parte teórica e ver como essas operações funcionam na prática. Acompanhe:
Como se faz a conta de Fatoração Completa?
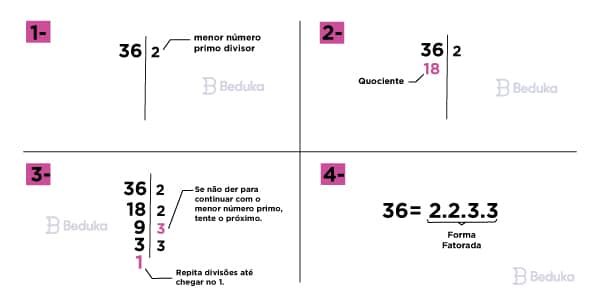
A Fatoração Completa é aquela que representa a decomposição total de um número. Para isso, vamos fazer a divisão desse número pelos menores número primo, até que seja impossível seguir com as contas.
O passo a passo é o seguinte:
- 1° Passo: Pegue o número que você irá fatorar e faça um traço vertical ao lado dele.
- 2° Passo: Divida-o pelo menor número primo possível e registre-o depois do traço.
- 3° Passo: Escreva o quociente da divisão (resultado) abaixo do número inicial.
- 4° Passo: Divida o quociente pelo menor número primo.
- 5° Passo: Repita o processo até que o quociente seja 1, ou seja, não há mais o que dividir.
Os números primos que ficarem depois do traço são os fatores. Se multiplicados, representam a fatoração do número inicial!
Repare na imagem acima, ela contém o exemplo resolvido e explicado!
- Você é uma daquelas pessoas que tem fome de conhecimento? Então siga o Beduka no Instagram para conteúdos diários!
Quais são os 7 tipos de fatoração?
Nós te dissemos que esse processo pode ser usado para três coisas principais e já te mostramos uma delas. Agora, vamos falar sobre a Fatoração de Polinômios, aquela que nos ajuda a simplificá-los.
Existem 7 tipos mais comuns de fatoração, vamos vê-los agora.
1° – Fator comum em evidência
Esse tipo de fatoração é usado quando estamos lidando com uma expressão em que existe um fator que se repete em todos os termos do polinômio, seja número ou letra.
Esse fator será colocado em evidência (à frente de tudo) e todo o resto será colocado entre parênteses. Isso só pode ser feito se pegarmos o termo que não é evidência e o dividirmos pelo fator comum. Aí sim colocamos o resultado dentro do parêntesis.
Na prática, vamos fazer os seguintes passos:
- 1° Passo: Observe se existe um número ou letra que divide todos os coeficientes do polinômio ou algo que se repete em todos os termos.
- 2° Passo: Coloque os fatores comuns na frente dos parênteses.
- 3° Passo: Divida os fatores que sobraram pelo fator comum.
- 4° Passo: Coloque o resultado dessas divisões dentro dos parênteses.
Exemplo: Escreva a forma fatorada do polinômio 32x +16y +48.
Observe que o número 16 divide todos os termos dessa expressão, então será o fator comum.
16 ( _______ )
Agora, realizamos a divisão dos termos 32x +16y +48. O resultado será:
16 (2x +y +3)
Essa é a forma fatorada!
2° – Agrupamento de semelhantes
Se você se deparar com um polinômio que não tenha um fator comum, uma alternativa é usar a Fatoração por Agrupamento.
É como se fizéssemos vários fatores comuns, cada um no seu grupinho. O primeiro passo é identificar os termos que podem ser agrupados e repetimos os mesmos passos anteriores.
Exemplo: Descubra a forma fatorada de mx + 4nx + my + 4ny.
Cuidado! Não podemos simplesmente somar. Note que cada um desses termos está multiplicado por coisas diferentes (y e x ou m e n).
O que nos resta é ver quais termos possuem fatores comuns e escolher um deles para colocar em evidência.
x (m+4n) + y (m+4n)
Não acabou! Observe com atenção, o termo (m+4n) se repete nos dois membros. Então novamente colocaremos em evidência.
(m+4n) (x+y)
Agora sim encontramos a forma fatorada!
3° Caso: Trinômio Quadrado Perfeito
Um trinômio é aquele polinômio formado por três monômios diferentes, ou seja, que não possuem fatores comuns.
É uma certeza matemática que, ao desenvolver o quadrado da soma de dois termos, como o, o resultado sempre será um trinômio quadrado perfeito.
Por isso, seguindo o raciocínio inverno, sabemos que a forma fatorada de um Trinômio Quadrado Perfeito é o quadrado da soma de dois termos!
Parece um pouco redundante, mas é isso mesmo.
- Porque tem esse nome “trinômio quadrado perfeito?”
Bom, o nome é para ilustrar os passos que usamos para saber se realmente se trata de um trinômio quadrado perfeito. Esses passos são:
- 1º Passo: Calcule a raiz quadrada do que está elevado ao quadrado.
- 2º Passo: Multiplique os valores encontrados por 2.
- 3º Passo: Comparar esses valores com o termo do meio, que não apresenta quadrados.
- 4° Passo: Se forem valores iguais, significa que é um quadrado perfeito.
Exemplo: Calcule a forma fatorada do trinômio X² + 24x + 144
Vamos conferir se ele é mesmo perfeito:
A raiz de x² é x
A raiz de 144 é 12
x . 12 . 2 = 24x
Já confirmamos que é mesmo perfeito, então sua forma fatorada será o quadrado das somas:
(x + 12)²
4° Caso: Trinômio quadrado imperfeito do tipo ax² + bx + c
Pode ser que você esteja resolvendo um trinômio do tipo ax² + bx + c e veja que ele não é perfeito.
Pode ficar tranquilo, é possível encontrar sua forma fatorada ao descobrir suas raízes. Isso significa que precisamos encontrar qual é o valor que, substituído em x, irá zerar a expressão.
Para isso, o mais comum é usarmos o Método de Bhaskara, o mesmo que é usado nas Equações de Segundo Grau!
5° Caso: Diferença entre dois quadrados
Agora, vamos trabalhar com as expressões que são formadas por dois monômios que se subtraem, sendo que cada um deles está elevado ao quadrado.
Nesse caso, nós precisamos decompor os quadrados em dois membros que se multiplicam e estão limitados por parênteses. Dentro do primeiro parênteses teremos a soma de suas raízes quadradas. Dentro do segundo, teremos a subtração delas.
Isso acontece porque a raiz quadrada é a operação inversa da potenciação de expoente 2.
Resumindo: quando fatoramos a² – b² precisamos encontrar (a + b)(a – b).
Exemplo: Descubra a forma fatorada de 49x² – 81
A raiz quadrada de 49x² é 7x.
A raiz de 81 é 9
Portanto, encontramos a forma fatorada:
(7x + 9)(7x – 9)
- Você pode estar se perguntando “E a soma dos quadrados?”.
A soma de dois quadrados é exatamente o resultado da fatoração de um trinômio quadrado perfeito. Um é o inverso do outro, então você já viu o que fazer!
6° Caso: Soma entre dois cubos
Como você deve imaginar, estamos falando dos polinômios elevados ao cubo, ou seja, ao expoente 3. Vamos trabalhar dois monômios que se somam, sendo que cada um deles está elevado ao cubo.
Em resumo, a fatoração de x³ + y³ resultará na forma (x + y)(x² – xy + y²).
Exemplo: Fatore a expressão 8x³ – 27
Primeiro, tiramos as raízes cúbicas, que são o oposto da operação de elevar ao cubo.
8x³ vira 2x
27 vira 3
Com isso, já temos os termo do primeiro membro. Só falta encontrar o quadrado deles para preencher o segundo.
(2x)² = 4x²
(3)² = 9
Logo, descobrimos que a forma fatorada é:
(2x + 3) (4x² – 36x² + 9)
7° Caso: Diferença entre dois cubos
Finalmente, vamos trabalhar com dois monômios que se subtraem, sendo que cada um deles está elevado ao cubo.
Em resumo, a fatoração de x³ – y³ resultará na forma (x – y)(x² + xy + y²).
Note que é muito semelhante à soma, a diferença é que os 2 primeiros sinais são invertidos.
Exemplo: Fatore a expressão 8x³ + 27
Primeiro, tiramos as raízes cúbicas, que são o oposto da operação de elevar ao cubo.
8x³ vira 2x
27 vira 3
Com isso, já temos os termo do primeiro membro. Só falta encontrar o quadrado deles para preencher o segundo.
(2x)² = 4x²
(3)² = 9
Logo, descobrimos que a forma fatorada é:
(2x – 3) (4x² + 36x² + 9)
Encontrando os divisores e múltiplos de um número com Fatoração
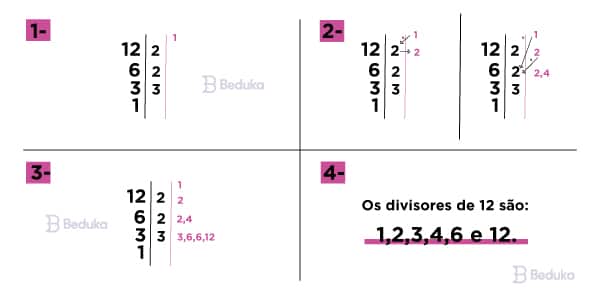
A última coisa que precisamos saber sobre Fatoração é como encontrar o MDC e MMC dos números. Veja os passos que precisamos dar para encontrá-los:
- 1° Passo: Comece fatorando o número completamente
- 2° Passo: Depois, trace uma segunda linha à direita dos números primos. Essa linha deve ser paralela à primeira. Anote os divisores depois dessa linha.
- 3° Passo: Coloque o número 1 no alto da coluna dos divisores. Ele sempre é divisor de qualquer número, então começamos por ele com certeza.
- 4° Passo: Multiplique o divisor 1 pelo primeiro fator primo. Depois, anote o resultado abaixo do 1.
- 5° Passo: Observe que na coluna dos divisores nós teremos 2 valores. Agora você precisa multiplicar esses dois divisores, separadamente, pelo número primo seguinte. Anote os 2 resultados obtidos.
- 6° Passo: Faça isso até ter multiplicado todos os divisores encontrados anteriormente por cada número primo. Se houver divisores repetidos não tem problema, apenas conte-os 1 vez.
Eu sei que parece um pouco confuso, por isso, analise a imagem acima com o exemplo para você entender!
Fatoração pode ser uma ferramenta muito útil nos seus estudos de matemática! Por isso, a parceira Sifet disponibiliza uma calculadora de fatoração para você descobrir ou tirar uma dúvida com apenas um clique.
Gostou do nosso artigo sobre Fatoração? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet!





