Descubra o que é a Lei dos Cossenos e como usá-la para resolver problemas complexos

A Lei dos Cossenos é uma importante ferramenta matemática, muito usada para resolver problemas em triângulos. Ela também vai aparecer nos seus estudos da física durante o Ensino Médio e até na faculdade de engenharia, arquitetura e cartografia, se escolher seguir qualquer um desses caminhos.

Em resumo, essa lei estabelece uma fórmula que envolve lados e cossenos dos ângulos de um triângulo qualquer. Permitindo que sejam encontrados valores desconhecidos com base em algumas informações que a questão te der.

Neste artigo, vamos explorar com detalhes o que é a Lei dos Cossenos, o que ela diz, em quais casos podemos usar e como aplicá-la. Além disso, vamos resolver um exercício para te ajudar a lidar com a fórmula.

E para te ajudar mais ainda, saiba que você está a poucos cliques de baixar o nosso Plano de Estudos Mágico. Ele te guiará na jornada rumo à aprovação no Enem. Não deixe a oportunidade passar, adquira o seu agora!

Fizemos um resumo bem completo explicando o que é a Lei dos Cossenos. Clique em um dos tópicos desse resumo para ir direto ao assunto:

• O que é Cosseno?
• O que é a Lei dos Cossenos? (Conceito e utilidade)
• Qual é a fórmula da Lei dos Cossenos?
• Resumo da Lei dos Cossenos
• Exemplo e aplicação da Lei dos Cossenos

O que é Cosseno?

Seria inútil chegar aqui e começar a falar sobre o que é a Lei dos Cossenos se você sequer sabe o que é um cosseno, certo? Então vamos relembrar primeiro esse conceito para depois chegarmos onde queremos.

O Cosseno é apenas uma medida específica que podemos tirar de um ângulo. Ela funciona como se fosse um CPF do ângulo, porque é única para cada valor angular. Por isso também, cada ângulo sempre terá o mesmo cosseno, independente da situação.

E não é preciso um trabalho muito grande para calcular o cosseno de um ângulo não. Os matemáticos descobriram que basta dividir o cateto adjacente ao ângulo pela hipotenusa quando se está em um triângulo retângulo.

Acredite se puder, essa conta é muito útil. Se você estiver resolvendo uma questão onde precisa achar o x que é a hipotenusa, e você tem o valor do ângulo e do cateto adjacente, é só “jogar” na fórmula do cosseno.

Mas há um porém: essa fórmula só funciona no triângulo retângulo. Foi justamente desenvolvendo esse raciocínio para superar as limitações é que criaram a Lei dos Cossenos!

O que é a Lei dos Cossenos?

Matematicamente falando, a Lei dos Cossenos é uma relação métrica que relaciona a medida dos lados de um triângulo qualquer com o cosseno de um dos seus ângulos.

Para que ela serve?

Essa relação é muito útil para ajudar a calcular valores de ângulos e lados quando temos poucas informações. E ela pode ser usada em qualquer tipo de triângulo, seja obtusângulo ou acutângulo!

Pode usar a Lei dos Cossenos no triângulo retângulo?

Sim! O que acontece é que, quando você a aplica no triângulo retângulo, vira o Teorema de Pitágoras. E aí é mais rápido e fácil usar ele. Mas é você quem escolhe!

O que diz a Lei dos Cossenos?

“Em qualquer triângulo, o quadrado de um dos lados corresponde à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles.”

Traduzir esse tanto de palavras pode parecer que é mais difícil do que falar Mandarim, mas os matemáticos já traduziram isso em fórmulas.

E fica mais fácil de entender, olhe no próximo tópico!

Qual é a fórmula da Lei dos Cossenos?

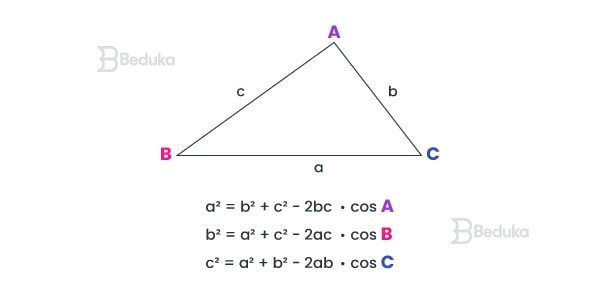
A fórmula da Lei dos Cossenos são essas três aí em cima na imagem.

Mas fique tranquilo, você não precisa decorar todas!

Na verdade, você deve ter observado que elas seguem o mesmo padrão. É que se trata de uma única fórmula que está sendo expressada para cada um dos três ângulos do triângulo. 

Basta você decorar uma e substituir nos lugares certos conforme a necessidade da questão, combinado?

Agora vamos ver alguns exemplos na prática de como usar isso!

Resumo do que é a Lei dos Cossenos

• A Lei dos Cossenos é uma relação métrica que envolve lados de um triângulo qualquer o cosseno de um de seus ângulos
• É usada em problemas em que conhecemos dois lados e o ângulo entre eles, mas precisamos descobrir o terceiro lado.
• Também é possível usar quando conhecemos os três lados do triângulo, mas precisamos calcular um de seus ângulos.

Lembre-se que é muito importante estudar matemática fazendo exercícios. Por isso, não deixe de usar o Simulado Enem Gratuito e Online que o Beduka preparou para você!

Exemplo de aplicação da Lei dos Cossenos

1- Um triângulo ABC tem o lado “a” medindo 12 cm e o lado “b” medindo 16 cm. Entre eles, há um ângulo de 60°. Descubra quanto mede o terceiro lado “c”.

Solução

Já segura a vontade de usar pitágoras, porque o enunciado não disse que era um triângulo retângulo… O que te resta é usar a Lei dos Cossenos! 

Vamos começar organizando os dados que temos:

(Esse é um dos ângulos notáveis, é bom saber o valor de cór ou olhar na tabela. Também é importante ver sua posição no ciclo trigonométrico para definir se o sinal será negativo ou positivo)

Agora é só substituir corretamente esses valores na fórmula:

c² = 12² + 16² – 2 . 12 . 16 . (1/2)
c² = 144 + 256 – 192
c² = 208
c = √208
c ≅ 14,5

Logo, o terceiro lado mede aproximadamente 14,5 cm.

Gostou do nosso resumo sobre o que é a Lei dos Cossenos? Compartilhe com os seus amigos e comente abaixo sobre algo que você deseja mais explicações.

Nós também queremos te conectar à faculdade! Experimente fazer o Teste vocacional ou procurar uma bolsa de estudos para o curso dos sonhos no Beduka Bolsas.

Boa sorte!