Você conhece as representações gráficas formadas por infinitos pontos que não fazem curva e são unidimensionais? Essas são as retas! Leia o nosso resumo com os seus tipos e fórmulas. Ao final, resolva os exercícios sobre Retas e confira seu desempenho com o gabarito!
Quer seguir diretamente para alguma parte? Clique em um dos tópicos abaixo:
- O que são Retas?
- Quais são os tipos de retas?
- Quais são as fórmulas das retas?
- Os 10 melhores exercícios sobre Retas!
- Gabarito das questões sobre Retas.
Quando você terminar os exercícios de Retas, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil!
O que são Retas?
Na Geometria Plana, as retas são definidas como o conjunto de pontos em sequência. Isso significa que elas são um traço que não faz curva.
Já que todo o espaço possui inúmeros pontos possíveis, concluímos que as retas são infinitas. Não tem começo nem fim.
Também podemos afirmar que as retas são unidimensionais. Em outras palavras, só medimos o seu comprimento e não conseguimos encontrar valores para profundidade ou altura.
Note que é preciso ter, no mínimo, dois pontos para formar uma reta. Além disso, a reta que passa por esses dois pontos (A e B) é uma reta específica (a reta r). A reta que passa pelos pontos A e D, por exemplo, é outra.
Com isso, concluímos que por um ponto qualquer e sozinho, podem passar infinitas retas. Porém, quando determinamos os demais pontos, estamos identificando uma reta específica.
Dependendo de onde esses pontos estão alinhados, as retas podem estar em 3 posições diferentes: horizontal, vertical ou inclinada.
- São mais de 200 resumos no instagram do Beduka!
Quais são os tipos de retas que existem?
Comparando duas ou mais retas, podemos classificá-las assim:
- Concorrentes: se cruzam em apenas um ponto, formando ângulos. Quando o ângulo formado é de 90°, recebem o nome de perpendiculares. Se não for, recebe o nome de oblíqua.
- Paralelas: não se cruzam nunca, nem se forem prolongadas. Isso significa que possuem a mesma inclinação em relação ao chão.
- Coincidentes: possuem os pontos em comum, então estão sobrepostas.
- Transversais: duas paralelas cortadas por uma terceira reta oblíqua. Seu ângulos têm propriedades de congruência.
- Coplanares: estão presentes no mesmo plano, ou seja, no mesmo universo geométrico.
- Reversas: estão presentes em diferentes planos, não estão no mesmo universo.
Você pode encontrar uma descrição completa com exemplos e imagens no nosso resumo sobre Retas!
Quais são as fórmulas das retas?
Esse assunto pertence à Geometria Analítica, matéria em que se relaciona geometria com álgebra.
Agora, nós só vamos te mostrar as duas fórmulas mais comuns sobre as retas, mas não deixe de ler nosso artigo sobre Geometria Analítica, pois ele tem as informações completas!
Equação Geral da Reta
ax + by + c = 0
Nesta fórmula, os números dos pontos que a compõem são colocados no lugar de “x” e “y”, referindo às coordenadas. “a”, “b” e “c” são coeficientes que determinam outras características, como inclinação.
Na realidade, nós temos o costume de usar mais a fórmula reduzida, que é um resumo desta. Vamos vê-la:
Equação Reduzida da Reta
A equação reduzida da reta é a usada nas funções de 1° grau, dada por:
y = mx + n
Para encontrar a equação reduzida de uma reta, é necessário descobrir os valores do coeficientes m e n e montar a equação final!
O coeficiente linear (n) é simples: basta saber que ele é o valor da ordenada (y) quando x = 0. Isso significa que n é onde a reta corta o eixo y, o ponto (0,n).
Para calcular o coeficiente angular (m) da reta, existem duas possibilidades:
- Saber que ele é igual à tangente do ângulo α:
m = tg α
- Usar a fórmula quando se tem dois pontos coordenados da reta:
Seja A(x1,y1) e B (x2,y2), então o coeficiente angular pode ser calculado por:
m = y2 – y1 / x2 – x1
Há ainda a possibilidade de encontrar o valor do coeficiente angular (m) e conhecer um ponto.
Os 10 exercícios sobre Retas!
Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.
Obrigado por ter lido até aqui!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM.
Questão 1- (UFRN)
Na figura a seguir, tem-se o gráfico de uma reta que representa a quantidade, medida em mL, de um medicamento que uma pessoa deve tomar em função de seu peso, dado em kgf, para tratamento de determinada infecção.
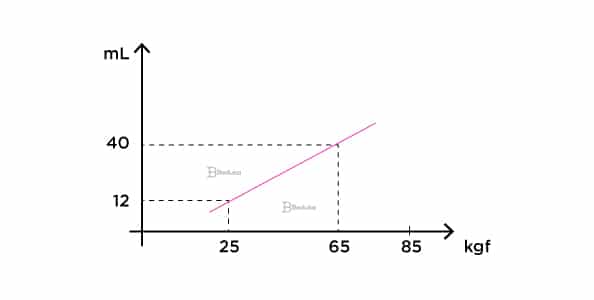
O medicamento deverá ser aplicado em seis doses. Assim, uma pessoa que pesa 85 kgf receberá em cada dose:
a) 7 mL.
b) 9 mL.
c) 8 mL.
d) 10 mL.
Questão 2- (FCC)
Na figura abaixo tem-se r//s; t e u são transversais. O valor de x + y é:
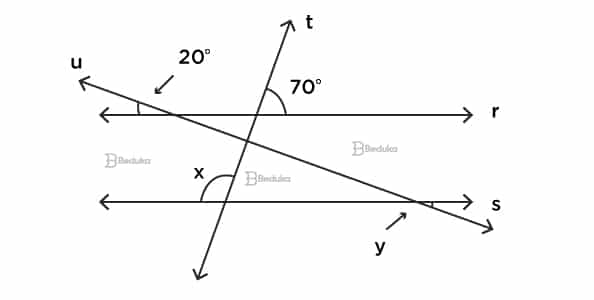
a) 100°.
b) 120°.
c) 130°.
d) 140°.
e) 150°.
- Você já fez 20% das questões sobre Retas. Continue assim!
Questão 3- (Cesgranrio)
A equação da reta mostrada na figura a seguir é:
a) 3x + 4y – 12 = 0.
b) 3x – 4y + 12 = 0.
c) 4x + 3y + 12 = 0.
d) 4x – 3y – 12 = 0.
e) 4x – 3y + 12 = 0.
Questão 4- (UFES)
Uma transversal intercepta duas paralelas formando ângulos alternos internos expressos em graus por (5x + 8) e (7x – 12). A soma das medidas desses ângulos é:
a) 40°.
b) 58°.
c) 80°.
d) 116°.
e) 150°.
Questão 5- (Uel)
As retas de equações x-2y+1=0 e -x-2y-1=0 são:
a) concorrentes e não perpendiculares entre si.
b) paralelas e não coincidentes.
c) perpendiculares entre si.
d) coincidentes.
e) ortogonais.
Nossa! Você já fez metade das questões de Retas. Vamos lá!
Questão 6- (UFMG)
Observe a figura.
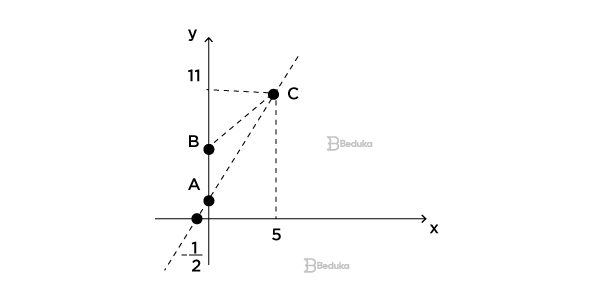
Nessa figura, a reta AC intercepta o eixo das abscissas no ponto (-1/2, 0 ), e a área do triângulo de vértices A, B e C é 10. Então, a ordenada do ponto B é
a) 20/11.
b) 31/11.
c) 4.
d) 5.
e) 6.
Questão 7- (FEI)
As retas 2x – y = 3 e 2x + ay = 5 são perpendiculares. Então:
a) a = -1.
b) a = 1.
c) a = -4.
d) a = 4.
e) n.d.a.
Questão 8- (Unitau)
A equação da reta que passa pelos pontos (3,3) e (6,6) é:
a) y = x.
b) y = 3x.
c) y = 6x.
d) 2y = x.
e) 6y = x.
- Ufa! Agora só faltam mais dois exercícios de Retas!
Questão 9- (USP)
A equação da reta que passa pelo ponto (3; 4) e é paralela à bissetriz do 2° quadrante é:
a) y = z – 1.
b) x + y – 7 = 0.
c) y = x + 7.
d) 3x + 6y = 3.
e) n.d.a.
Questão 10- (Unesp)
Seja A a intersecção das retas r, de equação y=2x, e s, de equação y=4x-2. Se B e C são as intersecções respectivas dessas retas com o eixo das abscissas, a área do triângulo ABC é:
a) 1/2.
b) 1.
c) 2.
d) 3.
e) 4.
- Parabéns, você fez todos os exercícios sobre Retas. Confira agora o Gabarito:
Gabarito das questões sobre Retas
Exercício resolvido da questão 1 –
Alternativa correta: b) 9 mL.
Exercício resolvido da questão 2 –
Alternativa correta: c) 130°.
Exercício resolvido da questão 3 –
Alternativa correta: b) 3x – 4y + 12 = 0.
Exercício resolvido da questão 4 –
Alternativa correta: d) 116°.
Exercício resolvido da questão 5 –
Alternativa correta: a) concorrentes e não perpendiculares entre si.
Exercício resolvido da questão 6 –
Alternativa correta: d) 5.
Exercício resolvido da questão 7 –
Alternativa correta: d) a = 4.
Exercício resolvido da questão 8 –
Alternativa correta: a) y = x.
Exercício resolvido da questão 9 –
Alternativa correta: b) x + y – 7 = 0.
Exercício resolvido da questão 10 –
Alternativa correta: a) 1/2.
- Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos exercícios sobre Retas? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.





