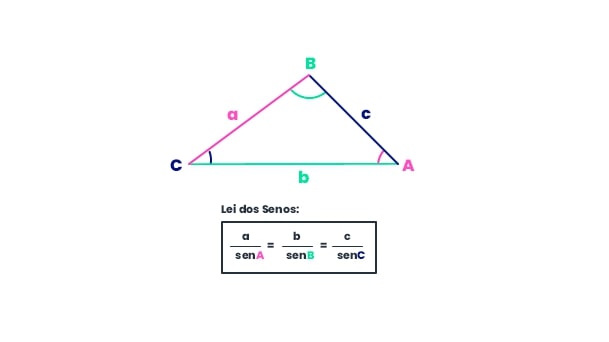
A Lei dos Senos é uma importante ferramenta matemática na hora de resolver problemas com triângulos. Essa lei estabelece uma relação de proporcionalidade entre os lados de um triângulo e os senos dos ângulos opostos a eles.
Por isso, os matemáticos desenvolveram uma fórmula que vai te ajudar a resolver questões onde você não tem todas as informações. Com isso, é possível achar o comprimento de um lado ou o valor de um ângulo que esteja faltando.
Neste artigo, vamos explorar em detalhes o que é a Lei dos Senos, como usar sua fórmula e resolver um exercício. Pois essa matéria é muito importante não só na matemática, mas também na física. Se você quer aprimorar seus conhecimentos, continue lendo!
E para te ajudar mais ainda, saiba que você está a poucos cliques de baixar o nosso Plano de Estudos Mágico. Ele te guiará na jornada rumo à aprovação no Enem. Não deixe a oportunidade passar, adquira o seu agora!
Fizemos um resumo bem completo explicando o que é a Lei dos Senos. Clique em um dos tópicos desse resumo para ir direto ao assunto:
- O que é Seno?
- O que é a Lei dos Senos? (Conceito e utilidade)
- Qual é a fórmula da Lei dos Senos?
- Resumo da Lei dos Senos
- Exemplo e aplicação da Lei dos Senos
O que é Seno?
Não dá para explicar o que é a Lei dos Senos se você nem sabe o que é um seno, então vamos começar do começo para esclarecer tudinho.
O Seno é uma medida específica que podemos tirar de um ângulo. Ela é única para cada ângulo, então ele sempre terá o mesmo valor de seno, não importa onde esteja. É como uma carteira de identidade!
Os matemáticos descobriram esse valor quando analisavam os ângulos em um triângulo retângulo. Bastou dividir o cateto oposto ao ângulo pela hipotenusa e encontraram o valor do seno.
Pode parecer sem sentido fazer essa conta, mas ela é muito útil. Se você estiver resolvendo uma questão onde x é a hipotenusa, mas você tem o valor do ângulo e do cateto oposto, é só “jogar” na fórmula do seno e achará o que falta.
Só que essa fórmula só funciona no triângulo retângulo, e é justamente por isso que surge a Lei dos Senos!
O que é a Lei dos Senos?
A Lei dos Senos é uma relação métrica que analisa a medida dos lados e ângulos de um triângulo qualquer, com base em sua proporcionalidade.
Para que ela serve?
Ela é útil pelo mesmo motivo que explicamos no tópico anterior: ajuda a calcular valores de ângulos e lados quando temos poucas informações.
O mais legal dessa lei é que você pode usá-la em qualquer tipo de triângulo, seja obtusângulo ou acutângulo!
Pode usar a Lei dos Senos no triângulo retângulo?
Sim! Você pode usar a Lei dos Senos em qualquer tipo de triângulo. Só que o Teorema de Pitágoras costuma ser usado neste caso por ser um caminho mais simples.
O que diz a Lei dos Senos?
“Em qualquer triângulo, a relação do seno de um ângulo é sempre proporcional à medida do lado oposto a esse ângulo.”
Essa é a definição formal do que é a lei dos Senos. Eu sei que essa definição parece aqueles problemas de lógica, mas quando a gente traduz isso tudo em fórmulas, fica mais fácil de entender.
Dá uma olhada no próximo tópico!
Qual é a fórmula da Lei dos Senos?
Não se assuste!
Essa fórmula gigante só quer dizer que toda vez que você dividir a medida de um lado pelo seno do ângulo que é oposto a ela, resultará num mesmo valor.
E você pode fazer isso com qualquer um dos três lados que encontrará sempre a mesma razão, porque é proporcional!
Às vezes você precisará até mesmo de uma mãozinha da regra de três para desenvolver a fórmula.
Atenção! É importante ressaltar que é preciso tomar cuidado na hora de usar essa lei para achar um ângulo.
Por se tratar de um cálculo, pode ser que o problema termine com uma raiz que dê dois valores: um positivo e outro negativo. Aí você terá que analisar para ver qual das duas respostas numéricas faz mais sentido naquele contexto.
Agora vamos ver um exemplo na prática de fazer isso!
Resumo do que é a Lei dos Senos
- A Lei dos Senos é uma relação métrica que envolve lados e ângulos de um triângulo qualquer, com base em sua proporcionalidade.
- É usada em problemas em que conhecemos dois ângulos e um lado que seja oposto a um deles.
- Também é possível usar quando conhecemos dois lados e um dos ângulos opostos a ele. Mas é preciso tomar cuidado neste caso.
Lembre-se que é muito importante estudar matemática fazendo exercícios. Por isso, não deixe de usar o Simulado Enem Gratuito e Online que o Beduka preparou para você!
Exercício de aplicação do que é a Lei dos Senos
1- Um homem tentou atravessar um rio de largura 100 m em linha reta, perpendicularmente ao rio. Se tivesse conseguido, ele teria saído do ponto A e chegado à B. Porém, a correnteza fez com que o barco viajasse numa inclinação de 30° em relação a A, por isso ele acabou percorrendo 160 m. Como consequência, o homem chegou à outra margem no ponto C, inclinado 45° em relação a B. Qual é a distância entre o ponto B e C?
Considere que é um rio real e que possui uma curvatura na margem, portanto, não se pode dizer que o ponto B e C estejam alinhados perpendicularmente.
Considere √2 = 1,4.
Solução:
Já segura a vontade de usar pitágoras, porque o enunciado deixou claro que o desenho dessa situação não formará um triângulo retângulo. O que te resta é usar a Lei dos Senos!
Vamos começar organizando os dados que temos:
Lado b (largura do rio) = 100 m
Lado c (trajetória real do barco) = 160 m
Lado a (o que eu quero achar) = ? m
Sen A = Sen 30° = 1/2
Sen C = Sen 45° = √2/2
Esses são ângulos notáveis, então é bom saber o valor de cór ou olhar na tabela. Também é importante ver sua posição no ciclo trigonométrico para definir se o sinal será negativo ou positivo.
Agora é só substituir corretamente esses valores na fórmula:
a / ½ = 160 / √2/2
2a = 320 / √2
2a = √2.320 / 3
2a = 106,6.√2
2a = 127,92
a = 63,96 m
Logo, o homem desceu a uma distância de 63,96 m do ponto que queria.
Gostou do nosso resumo sobre o que é a Lei dos Senos? Compartilhe com os seus amigos e comente abaixo sobre algo que você deseja mais explicações.
Nós também queremos te conectar à faculdade! Experimente fazer o Teste vocacional ou procurar uma bolsa de estudos para o curso dos sonhos no Beduka Bolsas.
Boa sorte!





