Radiciação: tudo o que você precisa para lidar com ela!

A Radiciação é uma operação matemática que usamos para descobrir a raiz de um número, seja a raiz quadrada ou cúbica. Ela é inversa à potenciação, isso significa que buscamos descobrir qual é o número que foi multiplicado por ele mesmo e quantas vezes, até que resultasse no número que nos foi dado.

Neste artigo sobre radiciação, você encontrará:

1. O que é Radiciação: símbolo e exemplos
2. Como calcular raiz com Fatoração
3. 6 Propriedades da radiciação + exemplo
4. Operações com radicais (multiplicação, divisão, soma e subtração)

• Estudando para as provas? Conheça O melhor Simulado do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!

O que é Radiciação?

A Radiciação é a operação matemática que nos permite encontrar a raiz de um número. O símbolo que marca essa operação é “√”. 

Você deve se lembrar que o oposto da adição é a subtração e que o oposto da multiplicação é a divisão. 

Da mesma forma, a radiciação é a operação oposta à potenciação. Por isso, é necessário que você conheça a potenciação antes de ler esse artigo!

Apenas para recapitular, vamos lembrar que a potenciação é definida como:

“A Potenciação é uma operação usada para multiplicar vários números iguais, ou seja, quando queremos multiplicar um número várias vezes por ele mesmo. O algarismo a ser multiplicado é a base e a quantidade de vezes é indicada no expoente.”

Se a radiciação é o contrário, então definimos que:

“A radiciação é uma operação em que descobrimos qual foi o número multiplicado e quantas vezes, para chegar ao número que já nos foi dado” 

• A radiciação serve para responder às perguntas do tipo: “Qual é o número que multiplicado por ele mesmo 3 vezes resulta em 125?” Por tentativa, podemos descobrir que é o número 5, mas há uma forma de representar isso em potências e raízes.

Símbolo da Radiciação e leitura da operação

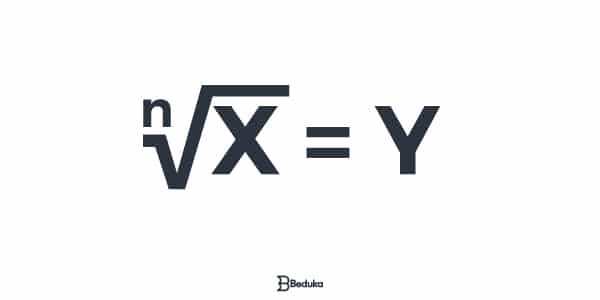
Para indicar a radiciação, usamos símbolo acima, sendo que:

• n → é chamado de índice, ele indica quantas vezes o número que estamos procurando foi multiplicado por ele mesmo
• X → é chamado de radicando, ele indica o resultado da potenciação feita, normalmente é o número que já nos foi dado.
• Y → é o resultado, o número que estamos procurando e que foi a antiga base da potenciação realizada.

Agora veja como fazemos a leitura dessa operação:

• ²√64 → lemos “raiz quadrada de 64”. Portanto, sempre que o índice da raiz for 2, diremos que é quadrada. A raiz quadrada é a mais comum, então ela pode vir representada apenas com o símbolo de raiz “√”, sem o índice “2” explícito.
• ³√8 → lemos “raiz cúbica de 8”. Portanto, sempre que o índice for 3, diremos que é cúbica.
• ²³√564 → lemos “vigésima terceira raiz de 564”. Do índice 4 em diante não há nomes específicos, dizemos apenas o ordinal do número: quarta raiz, quinta raiz, etc.

Exemplos de radiciação

Se pegarmos a potência 4³, sabemos que 4³ = 4 x 4 x 4 e que seu resultado é igual a 64. Para fazermos a operação contrária, precisamos da radiciação. Ela é escrita assim:

 ³√64 = 4

Quando dizemos raiz cúbica de 64, estamos buscando um número que foi multiplicado por ele mesmo 3 vezes e que o resultado é 64. 

Então, conseguimos enxergar que o 64 tem como raiz cúbica o número 4.

Se queremos descobrir a raiz quadrada de 64, estamos buscando um número que foi multiplicado por ele mesmo 2 vezes e resultou em 64. Basta observar a potência 8² = 8 x 8 = 64. Então, podemos dizer que:  

²√64 = 8

• Importante!

Um número tem raiz exata quando o resultado da radiciação é um número inteiro (sem casas decimais).

Você percebeu que o número 64 tem raiz quadrada e cúbica exatas, mas nem sempre é assim. Alguns números podem ter apenas uma dessas raízes exatas.

Não se preocupe quando aparecer uma raiz não exata! Os professores costumam dar esses valores por escrito ou permitem o uso de calculadora para encontrá-los.

Como calcular uma raiz? (Fatoração)

Até agora ficou tudo muito fácil porque tínhamos a potência escrita e bastava transformar no contrário. 

Mas o que fazer quando nos for pedido a raiz de um número e não soubermos a potência?

Neste caso, fazemos a fatoração do número! 

Nesse processo, pegamos o valor e vamos dividindo ele e seus resultados pelos menores número primos que conseguirmos, até que chegue a 1.

Veja:

1° Exemplo: determine a raiz quadrada de 144 

Para fazer √144 sem ter uma potência, precisamos fatorar. Observe a imagem acima!

Agora que já está fatorado, precisamos ver quais números se repetem em grupos de 2 (pares). Isso porque a raiz é quadrada (índice 2).

Por fim, vemos que que há 2 pares de número “2” e 1 par de número “3”. 

Com isso, vamos multiplicar os pares formados: 2 x 2 x 3 = 12.

O resultado foi 12, então sabemos que a raiz quadrada de 144 é 12! 

2° Exemplo: determine a raiz cúbica de 8

Para fazer ³√8 sem ter uma potência, precisamos fatorar (imagem acima).

Agora que já está fatorado, precisamos ver quais números se repetem em grupos de 3  (trinca). Isso porque a raiz é cúbica (índice 3).

Por fim, vemos que há apenas 1 trinca de número “2” 

Com isso, não há por quem multiplicar, existe apenas essa trinca valendo “2”.

O resultado foi 2, então sabemos que a raiz cúbica de 8 é 2! 

3° Exemplo: determine a raiz quadrada de 200

Para fazer √200 sem ter uma potência, precisamos fatorar (imagem acima).

Agora que já está fatorado, precisamos ver quais números se repetem em pares, pois a raiz é quadrada (índice 2).

Por fim, vemos que há 1 par do número “5”, 1 par do número “2” e sobra um “2” sem par.

Com isso, vamos multiplicar apenas os pares formados, enquanto o que ficou sem par deve permanecer dentro da raiz.

5 x 2 = 10. 

O resultado foi 10 fora da raiz e um 2 dentro da raiz. Então sabemos que a raiz quadrada de 200 é 10√2! 

• √2 não é uma raiz exata, por isso não conseguimos encontrar agora. Se você puder usar calculadora ou o professor te der o valor dela, basta multiplicar pelo 10 que está fora da raiz. Se não, escreva desse jeito acima!

As 6 propriedades da radiciação (exemplos)

As propriedades matemáticas são “atalhos” que podemos pegar para chegar ao resultado. Elas são deduções lógicas que, se decorarmos, é só bater o olho e escrever o resultado. Ela nos poupa do trabalho de resolver uma conta!

Veja quais são as propriedades da radiciação:

1° A raiz de um número n elevado a n é igual a esse mesmo número.

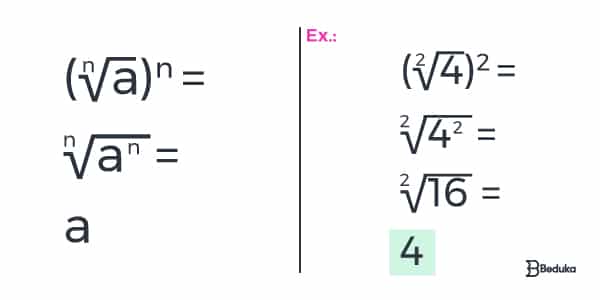
2 ° O Índice e o expoente do radicando podem ser multiplicados ou divididos pelo mesmo número, sem prejudicar o resultado.

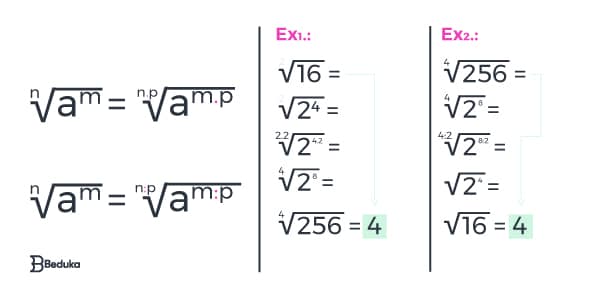
3 ° Para realizar a raiz de uma raiz, basta multiplicar seus índices. 

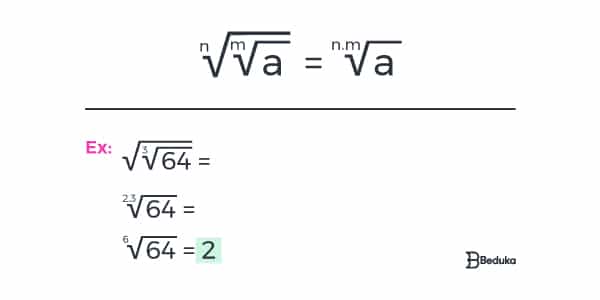
4° Na multiplicação ou divisão com radicais de mesmo índice realiza-se a operação com os radicandos e mantém-se o índice do radical.

5° Todo radical pode ser escrito na forma de potência.

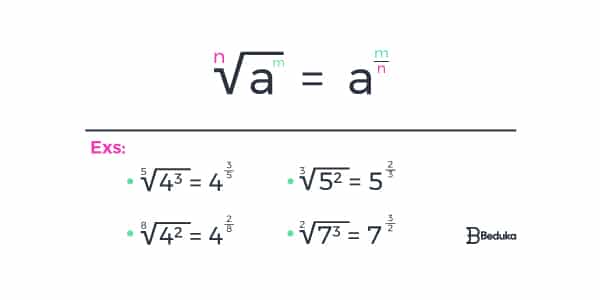
6° A potência da raiz pode ser transformada no expoente do radicando para que a raiz seja encontrada.

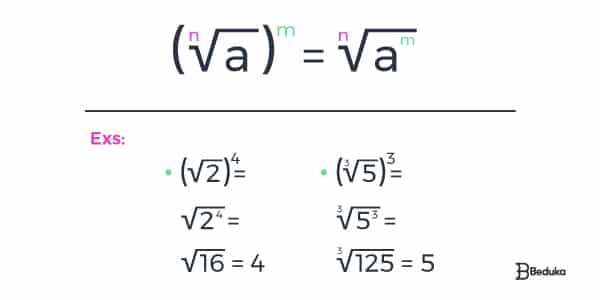
Operações com radicais ou raízes

Pode aparecer alguma expressão numérica que contenha as 4 operações básicas (adição, subtração, multiplicação e divisão) entre raízes. Para saber como resolver, veja os exemplos a seguir!

Lembre-se: caso aconteça de haver uma raiz no denominador de um número, precisaremos fazer a racionalização da fração!

Soma e Subtração

A regra para somar ou subtrair começa identificando qual o grau de semelhança entre os radicais, ou seja, se apresentam índice e radicando iguais. 

Pode ser que os radicais dados não estejam “limpos”, ou seja, precisaremos de simplificá-los antes de qualquer coisa. Após a simplificação é que veremos em qual caso se enquadra!

• 1º caso – Radicais semelhantes

Para somar ou subtrair radicais semelhantes, devemos repetir o radical e somar ou subtrair seus coeficientes.

• 2º caso – Radicais não são semelhantes

Calculamos os valores dos radicais individualmente e depois efetuamos a soma ou a subtração, se for possível.

Multiplicação e Divisão

A regra para multiplicação e divisão também começa identificando qual o grau de semelhança entre os radicais.

Pode ser que também seja necessário simplificá-los antes, mas você irá identificar na hora que se deparar com essas questões.

• 1º caso – Radicais com mesmo índice

Quando isso acontecer, basta repetir a raiz e realizar a operação com os radicandos.

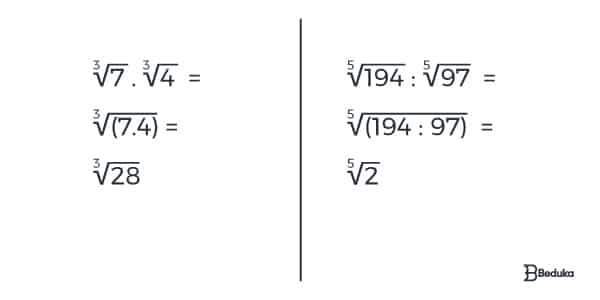
• 2º caso – Radicais com índices diferentes

Aqui, precisamos primeiro reduzir para chegar ao mesmo índice, depois realizar a operação com os radicandos.

Gostou do nosso artigo sobre Radiciação? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.

Experimente agora!