Racionalização de denominadores é conseguir simplificar uma fração que tem uma raiz no denominador. Na matemática, uma fração com raiz em baixo é um número irracional, então precisamos transformá-lo em racional. Para eliminar a raiz sem alterar o valor final da fração, descobrimos um número adequado para multiplicar em cima e em baixo.
Neste artigo sobre Racionalização, você encontrará:
- O que é e como funciona a Racionalização?
- Porque temos que racionalizar?
- Como fazer racionalização?
- Fator racionalizante, conjugado, raiz quadrada e somas
- Depois de ler o artigo, treine com os exercícios de racionalização!
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
O que é Racionalização?
A Racionalização de denominadores é um processo de cálculos matemáticos. Ela é um tipo de ferramenta para facilitar as contas que envolvem os denominadores incomuns nas frações.
Nós estamos acostumados a ver números racionais no denominador, tais como: “2”, “0,25”, “-4” ou no máximo “½”.
Mas, quando aparece algo diferente disso, precisamos recorrer à racionalização!
Porque temos que racionalizar?
No desenrolar de uma equação, podemos nos deparar com uma fração de denominador irracional, tal como uma raiz. Isso pode ser um impedimento para fazer a simplificação. Por isso, inventou-se o recurso chamado racionalização.
Esse processo nos permite achar uma fração equivalente que não tenha o problema da raiz no denominador.
Observe as frações 4/2 e 8/4 . Elas são formadas por números diferentes, mas quando resolvemos a divisão, o resultado é o mesmo: 2. Na fração equivalente a divisão resultará em um mesmo valor final, mesmo que os números sejam outros.
No caso da racionalização, o valor da primeira fração-problema será o mesmo que o da equivalente que encontraremos. Porém, os números que a compõem não serão mais irracionais, permitindo o desenrolar da simplificação.
Vamos entender como isso funciona:
Como funciona a Racionalização?
Como foi dito, a Racionalização funciona transformando um denominador irracional em um racional.
Para achar uma fração equivalente, é preciso realizar a mesma operação em ambos os membros da fração. Isso só funciona porque tanto o numerador quanto o denominador foram multiplicados ou divididos pelo mesmo número.
O número escolhido para isso é chamado de conjugado. O cálculo ficará mais fácil de compreender, como você verá no exemplo adiante!
O que é fator Racionalizante e Conjugado de um número?
Fator racionalizante ou Conjugado são os nomes do número que será multiplicado em ambos os termos para permitir que o denominador deixe de ser problemático.
Como fazer racionalização de raízes?
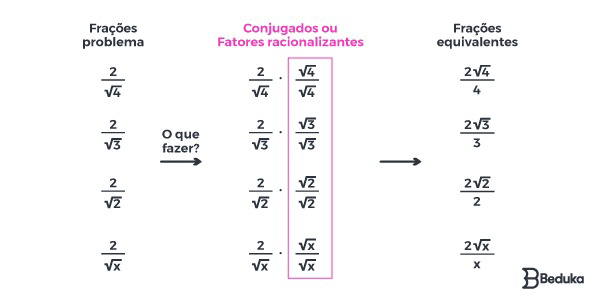
Como a maior parte dos números irracionais são raízes quadradas, precisamos que o conjugado elimine esta raiz.
Observe o exemplo:
- Note que conjugado de qualquer raiz quadrada sempre será a própria raiz quadrada. O resultado dessa multiplicação sempre será o número que estava dentro.
- Não há problema em deixar a raiz no numerador, ela só não pode ficar no denominador porque impede a simplificação. Se não for possível simplificar tudo, podemos deixar na forma mais reduzida possível.
- Lembre-se: uma raiz quadrada costuma ser indicada como ²√x . Porém, se não houver índice explícito, consideramos que também é quadrada (√x). Já a cúbica (³√x), ou índices maiores, precisam estar indicados numericamente.
Como fazer racionalização em casos especiais?
Portanto, podemos resumir que, para racionalizar o denominador-problema de uma fração, basta dar três passos:
- Encontrar o conjugado do denominador problema
- Multiplicar o conjugado pelos dois termos da fração para que seja equivalente
- Simplificar a fração encontrada, se for possível
Mas as coisas sempre podem complicar! Por isso, existem casos especiais com operação entre raízes ou índices não quadráticos. Acompanhe:
Racionalização de denominador com raiz não quadrada
Quando a raiz apresentar índice diferente de 2, o conjugado terá o mesmo índice da raiz. Porém, será necessário encontrar o expoente do número interno que, quando somado ao expoente do número inicial, resulte em um valor igual ao índice da raiz.
Isso porque quando multiplicamos raízes de mesmo índice e base, a regra é somar os expoentes. Com os expoentes iguais aos índices, podemos simplificá-los e tirar a raiz.
Confuso? Veja o exemplo:
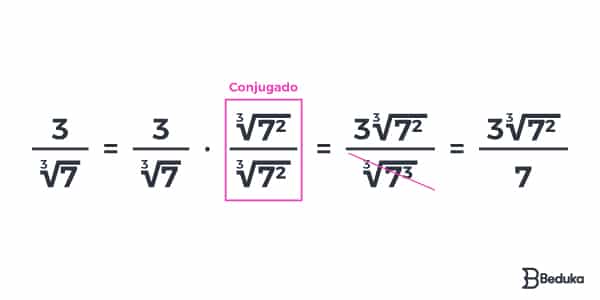
- Lembre-se: um número sem expoente explícito significa estar elevado ao 1. Por isso, temos dentro da raiz cúbica: 7¹ . 7² = 7³
Como racionalizar a soma de raízes?
Para finalizar, pode aparecer no denominador uma soma ou subtração de raízes quadradas! Mas calma, é mais simples do que aparenta: o conjugado será igual às raízes com a operação inversa.
Nesse caso, é preciso fazer isso porque utilizamos as propriedades do produto da soma pela diferença dos mesmos termos. Assim, se tivermos uma fração com denominador “√2 + √5”, basta arranjar um conjugado que seja “√2 – √5” para multiplicar.
Veja um exemplo completo:
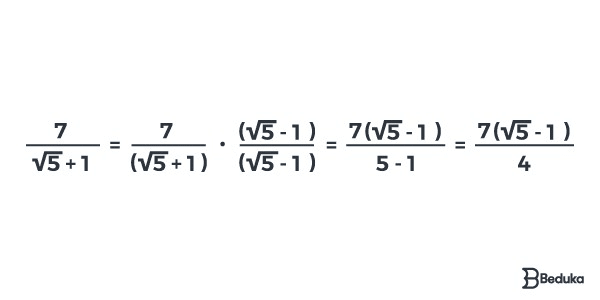
Gostou do nosso artigo sobre racionalização? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!







