A Decomposição de Vetores é uma operação matemática para encontrar as componentes verticais e horizontais de um vetor. A partir dela, descobrimos a projeção no eixo x e y do plano cartesiano. Usando a trigonometria, podemos determinar até mesmo o módulo!
Neste artigo sobre Decomposição de Vetores, você encontrará:
- O que são vetores e grandezas vetoriais
- Operações de soma (4 casos) e subtração com vetores
- Método poligonal, paralelogramo e lei dos cossenos
- Decomposição de Vetores: como fazer e utilidade
- Exemplo resolvido
- Estudando para as provas? Conheça O melhor Simulado do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!
O que são vetores e grandezas vetoriais
Você já deve ter ouvido falar em grandezas da química ou grandezas da física. No meio científico, a palavra grandeza se refere a tudo o que pode ser medido.
Na física, dizemos que existem 2 tipos de grandezas:
- Grandezas escalares: basta um número e sua unidade de medida para entendermos o que é medido. A massa (50 kg) ou a distância (50 m) são exemplos disso.
- Grandezas vetoriais: além do valor e sua unidade, precisamos também da direção e do sentido para entender a informação completa do que se mede. As forças físicas são exemplos disso.
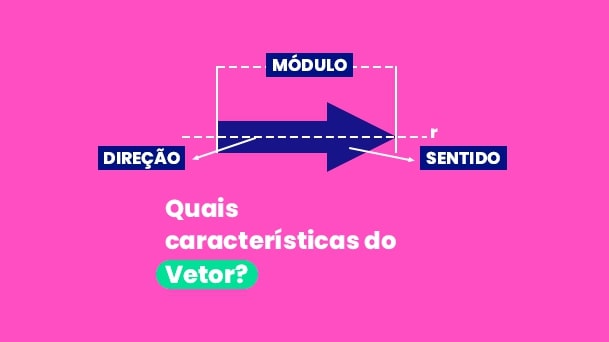
Para representar as informações completas das grandezas vetoriais criou-se os vetores. Os vetores são segmentos de reta orientados que possuem:
- Módulo: corresponde à intensidade da força, ou seja, o seu valor numérico.
- Direção: é a própria direção em que o corpo se move ou que a força atua. Pode ser na horizontal ou vertical.
- Sentido: equivale ao lado onde a força é aplicada. Cada direção possui dois sentidos, sendo eles esquerda e direita quando falamos em horizontal, positivo e negativo quando falamos em vertical.
Todos os vetores são definidos com essas três características ao mesmo tempo, é como um “nome completo”, permitindo sua identificação e diferenciação dos outros.
Operações com vetores
Em algum momento da sua vida escolar você já se trombou com as leis de Newton, com a cinemática e todas aquelas imagens cheias de setinhas.
Pois bem, as fórmulas que você encontra foram deduzidas através de vários fatores, incluindo a análise de vetores.
Mas nem tudo são fórmulas! Por isso, você deve ter feito algum exercício de Empuxo ou Atrito em que era preciso desenhar, encontrar a resultante e depois calcular!
Tudo o que você tem feito, mesmo sem perceber, são operações de soma ou subtração de vetores!
Soma vetorial
Somar é unir elementos… essa é fácil não é? Pois bem, você também pode juntar vetores e ver qual é o resultado final. Vamos explicar com exemplos para ficar mais fácil:
Caso 1: soma com mesma direção e sentido
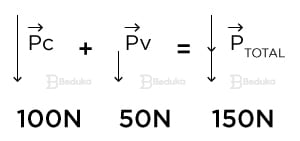
Vamos supor que um funcionário colocou um caixote sobre o chão. Já sabemos que o objeto exerce a força peso na superfície em que está posicionado. Se o caixote tem massa de 10 kg, sabemos que o peso gerado será de 100 N, vertical e para baixo.
Agora imagine que eu acrescentei um vaso em cima do caixote, de massa 5kg. Se eu quero saber qual é a força resultante no chão, eu preciso calcular a soma dos pesos do vaso com o do caixote.
Simples, não é? Só tem um detalhe que muda tudo:
Como estamos tratando de grandezas vetoriais, não basta somar os módulos, é preciso ver o que acontece com a direção e o sentido.
No exemplo acima, falamos de duas forças peso que sempre têm a mesma direção e sentido. Por isso, tínhamos dois vetores verticais para baixo, somando-os, obtemos o resultado igual a um vetor vertical para baixo de módulo 150 N.
Caso 2: soma com direção ou sentido diferente
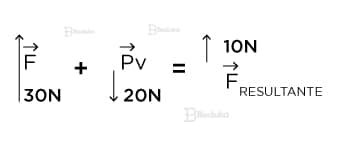
Quando você está com os braços estendidos tentando levantar um haltere de 2kg (pezinhos de metal) na academia, temos duas forças opostas atuando.
O haltere exerce um peso vertical para baixo (20 N) na sua mão e você exerce uma força vertical para cima (superior a 20N, vamos supor 30N) para conseguir levantá-lo.
Assim como no plano cartesiano, o que está para cima do eixo x é positivo e o que está abaixo dele é negativo. Também temos que à direita do eixo y é positivo e à esquerda dele é negativo.
Seguindo esse raciocínio, para realizar a soma vetorial de uma força vertical para baixo com uma vertical para cima, nós mantemos o módulo positivo da que aponta para cima e o somamos com um valor negativo da que aponta para baixo:
(+30N) + (-20N) = 10N
Assim, podemos dizer que a força resultante é de 10N vertical para cima, significando que o haltere está sendo levantado.
Não se preocupe se uma conta der um valor negativo, lembre-se que o sinal aponta apenas qual é o sentido!
Caso 3: soma com direção e sentido diferentes
Para ilustrar esse exemplo, vamos supor que 2 crianças estão brigando por uma boneca: Maria puxa para cima e Joana puxa para a direita.
Observe que os vetores são perpendiculares entre si, ou seja, formam um ângulo de 90°.
Nesse caso, nós precisaremos usar um dos dois métodos:
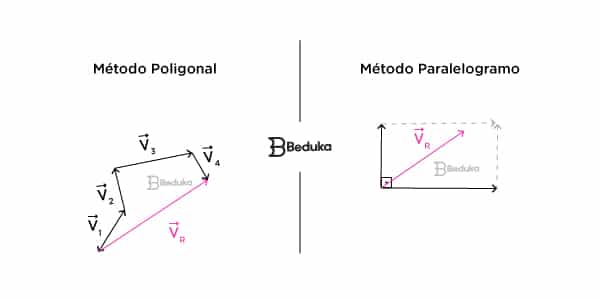
- Método da linha ou poligonal
Colocamos os vetores conectados, ou seja, a cabeça de um vetor encostará na origem do outro vetor e assim por diante.
Esse método pode ser feito usando vários vetores, o que importa é não alterarmos o seu tamanho, sentido e direção.
Depois de uní-los corretamente, o primeiro vetor colocado terá o seu final livre e o último terá a cabeça livre. Basta traçar uma linha partindo do rabo até a cabeça para descobrir qual é o sentido e direção do vetor resultante.
Normalmente eles são feitos em malhas quadriculadas, então você pode contar o número/ medida de quadradinhos para descobrir o módulo final.
- Regra do paralelogramo
Esse método é mais prático, rápido e ocupa menos espaço, mas só pode ser aplicado com 2 vetores por vez, quando formam um ângulo de 90° graus (perpendiculares).
Nesse caso, primeiro unimos as duas origens dos vetores. Depois, traçamos uma linha pontilhada perpendicular às cabeças dos vetores. Na realidade, elas representam a projeção de um vetor sobre o outro.
Esses prolongamentos se encontrarão e aí podemos traçar o resultado. O vetor resultante partirá da origem dos dois e sua cabeça terminará onde os prolongamentos se encontram.
Caso 4: Soma de vetores de qualquer direção com cálculo do módulo
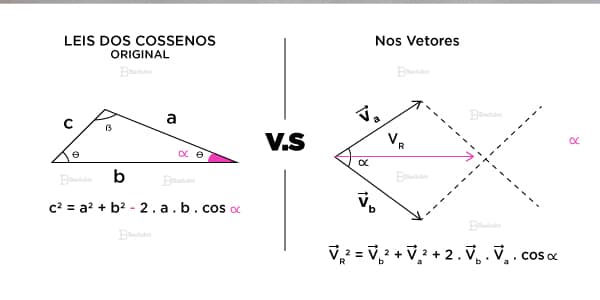
Como calcular qualquer par de vetores de qualquer direção e ainda saber o módulo por meio de contas? Primeiro usamos o método dos paralelogramos e depois aplicamos a Lei dos Cossenos!
Observe a imagem acima!
Note que, no caso das grandezas vetoriais, precisamos mudar o sinal original da lei (era negativo e passou a ser positivo).
Por que mudou o sinal? Porque esses vetores deveriam formar um triângulo como o indicado no original, e aí usaríamos a fórmula original.
Mas, aplicando o método do paralelogramo e deslocando os vetores para formar um triângulo, o ângulo de referência será superior a 90° e inferior a 180°.
Isso significa que, nessa faixa de valores, o cosseno de um número é sempre negativo. Por isso, invertemos o sinal da equação original.
Subtração vetorial
Se você já entendeu tudo da soma, certamente saberá fazer a subtração. Tudo o que você precisa lembrar é que a subtração é o oposto da soma.
Portanto, você pode manter o sinal de negativo para um dos vetores e realizar uma soma de acordo com o tipo de caso que se encaixar melhor!
- Você é uma daquelas pessoas que tem fome de conhecimento? Então siga o Beduka no Instagram para conteúdos diários!
Decomposição de vetores
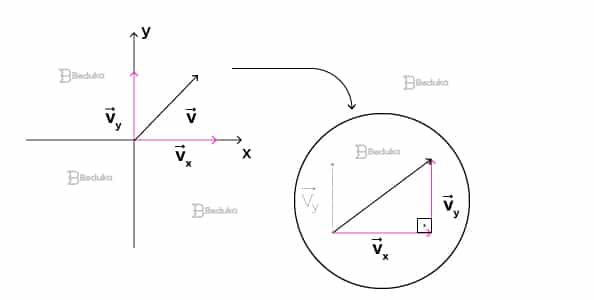
Você observou que a soma vetorial ocorre quando temos dois vetores e buscamos encontrar um resultante ao final. A decomposição vetorial é o processo inverso: temos um vetor e queremos descobrir quais os outros 2 que o geraram.
Assim, a decomposição é uma das operações realizadas com os vetores. Nela, definimos os seus componentes originais tendo como base os eixos x e y do plano cartesiano.
Por fim, entendemos que o nosso vetor V pode ser decomposto em vetores Vx e Vy. Se aplicarmos a soma vetorial pela regra do paralelogramo nos vetores Vx e Vy, ele nos trará de volta o V.
Como fazer decomposição de vetores?
Agora vamos aos cálculos!
Para decompor um vetor (determinar as componentes perpendiculares) basta seguir 4 passos:
- Posicionar o vetor no plano cartesiano, de modo que sua origem coincida com a origem do plano.
- Traçar uma linha pontilhada que sai da cabeça do vetor e é paralela ao eixo x.
- Traçar outra linha pontilhada paralela ao eixo y, que sai da cabeça do vetor.
- Ver até onde vai a projeção do vetor horizontal (Vx) e do vertical (Vy).
E se precisarmos saber os módulos?
Para isso, podemos mudar o vetor Vy de lugar para formar um triângulo retângulo. Depois, recorremos à Trigonometria do triângulo retângulo para resolver os cálculos e encontrar os valores!
Assim, chegamos às fórmulas:
Vy = V. senθ
e
Vx = V. cosθ
Como vou saber qual é a fórmula certa de usar?
Se um determinado lado do triângulo está com o ângulo, usamos a fórmula do cosseno. Se estiver sem (for cateto oposto), usa-se a fórmula do seno.
Por fim, sabemos que o Teorema de Pitágoras é aplicado em triângulos retângulos. Então podemos estabelecer mais uma fórmula:
V² = Vx² + Vy²
Quando a decomposição de vetores é útil?
A decomposição de vetores é usada quando lidamos com uma força ou grandezas vetoriais que estão “inclinadas”. Assim, forma-se um ângulo entre o vetor e o eixo x em que ele se apoia.
Com esses cálculos, descobrimos suas componentes e facilita nossos cálculos nas questões envolvendo atrito, cinemática, tração, empuxo, etc.
Exemplo resolvido de exercício com decomposição vetorial
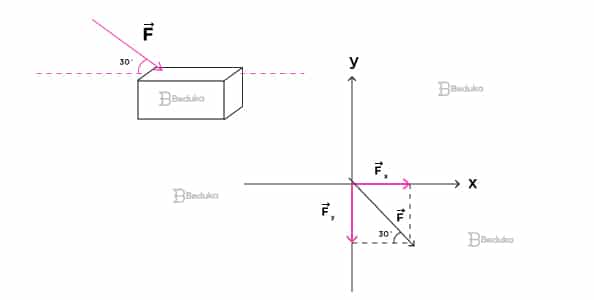
Imagine que Pedro aplicou uma força F de 100N em um bloco de 2kg que estava parado sob uma superfície plana. Essa força foi aplicada fazendo um ângulo de 30°, pois a posição da mão dele assim o fez.
Determine qual é o peso resultante que o bloco exerce na superfície, no momento em que Pedro aplica a força no bloco.
O cálculo de resolução é o seguinte:
Se o objeto pesava 2k, ele já exercia uma força peso de 20N naturalmente. Porém, Pedro pressionou o objeto com uma força de 100N.
Não podemos dizer que o peso resultante foi 120 porque a força aplicada por Pedro não era vertical para baixo, era inclinada em 30°.
Por isso, preciso somente do valor da componente vertical Fy do vetor F. Assim saberemos qual parte dessa força pressiona o objeto para baixo.
Fy = F. sen 30°
Fy = 100. Sen30º
Fy = 100 x 0,5
Fy = 50 N
Por isso, o peso resultante que o chão sofre enquanto Pedro pressiona o objeto, vale 50 + 20 = 70N.
Gostou do nosso artigo sobre Decomposição de Vetores? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet!