O Hexágono é uma figura plana que possui 6 lados. Este polígono pode ser convexo ou côncavo, regular ou irregular. Para entender mesmo a matéria, você precisa conhecer cada tipo, suas propriedades, as fórmulas de área e perímetro e como ele se relaciona com as figuras triangulares.
Neste artigo sobre Hexágono, você encontrará:
- O que é um Hexágono? Conceitos da geometria plana
- Tipos de hexágonos: regular, irregular, côncavo ou convexo
- Ângulos e propriedades
- Cálculo da área, perímetro e apótema
- Prismas e pirâmides de base hexagonal
- O hexágono na natureza
- Estudando para as provas? Conheça O melhor Simulado Enem do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!
O que é um hexágono?
O Hexágono é uma das várias figuras da Geometria Plana, aquelas que apresentam bidimensionalidade. Sua principal característica é ser um polígono de 6 lados. Se ele for do tipo regular, os seus lados serão todos iguais.
É muito conceito de uma vez?
Calma! Vamos te explicar cada coisa:
Geometria plana e polígonos
A geometria plana é a área da matemática que estuda as figuras planas e suas partes. Provavelmente você já ouviu falar nessas figuras: retângulos, círculos, triângulos, e a estrela da vez, os hexágonos!
Assim, os seus objetos de estudo são as formas que possuem duas dimensões (altura e largura), além dos conceitos de reta, área e ângulo.
As figuras planas são sempre uma região fechada formada por, no mínimo, 3 segmentos. Quando já temos uma figura formada, deixamos de falar “segmentos de reta” e chamamos de “lados”.
- Dentro desse grande grupo, temos uma divisão que separa as figuras planas poligonais e as não-poligonais.
Os polígonos são figuras planas de 3 ou mais lados com segmentos retos que não se cruzam. Suas extremidades se encontram formando ângulos!
As não-poligonais são como o círculo, que são formados pelas linhas. Diferentemente dos segmentos de retas, as linhas possuem formatos curvos.
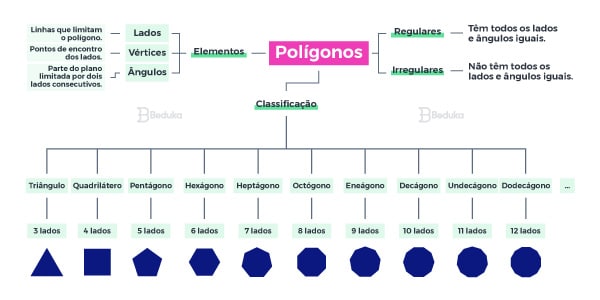
- Dependendo da quantidade de lados de um polígono, podemos dar nomes para eles.
O polígono de 3 lados se chama triângulo, o de 4 lados se chama quadrilátero, o de 5 lados é pentágono e o de 6 lados é hexágono.
Tipos de Hexágono: regularidade e concavidade
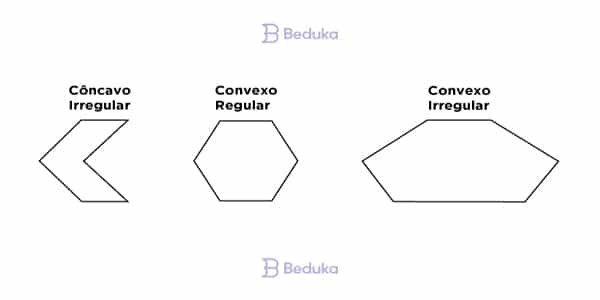
Você já deve ter ouvido falar em diferentes tipos de triângulos e quadriláteros. No caso dos Hexágonos, só podemos classificá-los quanto a dois aspectos:
- Regulares ou Irregulares: depende da presença ou ausência de simetria. Os que são simétricos são regulares e, automaticamente, sabemos que todos os seus lados são iguais (mesma medida). Os irregulares não têm essa propriedade.
- Côncavos ou Convexos: os hexágonos côncavos são aqueles com lados que formam uma “área para dentro”. Se traçamos retas entre seus vértices, veremos que algumas reta não passam por dentro da figura. Já nos convexos, todas as retas traçadas entre os vértices são parte da figura.
Em quase todos os casos, trabalhamos com os hexágonos convexos e regulares. Eles são clássicos nos vestibulares!
Ângulos nos hexágonos
Quanto aos ângulos, é importante lembrar que eles são a região formada entre duas retas (lados), determinando a inclinação entre elas.
A soma dos ângulos de um polígono de 4 ou mais lados sempre é 360°, então esse valor se aplica ao hexágono.
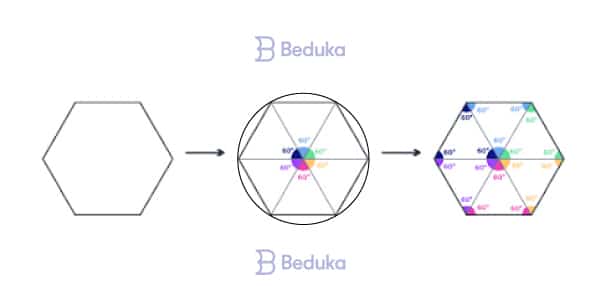
Mas a mágica acontece quando lidamos com um hexágono circunscrito (dentro de um círculo).
Nós sabemos que todos os raios do círculo são iguais. Observando a figura acima, deduzimos que o ângulo das partes de um hexágono regular e convexo sempre mede 60°! Basta fazer 360° dividido por 6 e entenderemos.
Agora note: se um hexágono regular, convexo e circunscrito é formado por 6 áreas triangulares de mesmo lado e ângulo, só podemos estar falando dos triângulos equiláteros!
Área e perímetro do hexágono
Perímetro e área são conceitos próprios da geometria plana e os usamos para medir diferentes elementos da figura. Você pode acessar o artigo Área, Perímetro e Volume para saber com detalhes.
Resumidamente, os conceitos são:
- Área (A): medida da superfície de uma figura.
Podemos dizer que é o preenchimento de uma figura plana. É como se você quisesse pintar uma folha inteira e calculasse quanto de tinta precisaria para cobrir tudo!
- Perímetro (2P): medida do contorno de uma figura.
Para enxergar o que estamos dizendo, basta que você se imagine pegando um barbante e contornando um caderno. Depois de marcar até onde foi com o barbante, você desenrola ele e mede na régua. O valor encontrado é o perímetro e o semiperímetro (P) é sua metade.
Como calcular a área dos hexágonos? (fórmulas)
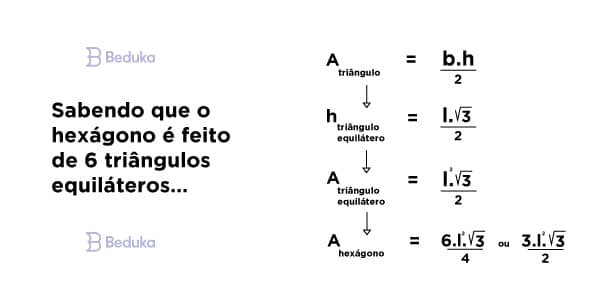
No tópico passado, nós chegamos à conclusão de que um hexágono é formado por 6 triângulos equiláteros. Por isso, não é preciso decorar uma fórmula do hexágono, mas simplesmente saber a do triângulo e multiplicar por 6!
A área (A) de um triângulo (t) qualquer é dada como “base vezes altura sobre 2”, assim:
A (t) = b.h / 2
A base (b) será o próprio valor do lado (l) do triângulo equilátero (t.eq.), pois todos eles são iguais. Só precisamos descobrir a altura (h) para achar a fórmula de sua área.
A altura do triângulo equilátero pode ser encontrada usando o teorema de pitágoras ou a trigonometria. Independente do meio escolhido, encontramos que altura é “lado vezes raiz de 3 sobre 2”, assim:
h (t.eq) = l.√3 / 2
Por fim, encontramos a fórmula que dá a área de um triângulo equilátero. Basta substituir o valor da altura na primeira fórmula:
A (t.eq) = b.( l.√3 / 2) / 2
A (t.eq) = l².√3 / 4
Finalmente, sabemos que a área de um hexágono regular será igual à soma das seis áreas dos triângulos equiláteros. Então podemos escrever que a fórmula da área do hexágono é:
A (hex) = 6 . l² . √3 / 4
Você ainda pode encontrar a fórmula simplificada, que dá no mesmo:
A (hex) = 3 . l² . √3 / 2
Perímetro do hexágono
O perímetro (2P) é a medida do contorno de todos os lados (l) de uma figura. Se o hexágono tem 6 lados, podemos dizer que:
2P (hex) = 6.l
Da mesma forma, o semiperímetro (P) é a metade do perímetro, então teremos:
P (hex) = 6.l / 2
P (hex) = 3.l
Apótema do hexágono
O apótema (a) do hexágono é o segmento de linha que liga o centro da figura até o ponto central ou ponto médio (divide ao meio) de um dos seus lados. Já que há 6 lados, podemos traçar 6 apótemas, cada um saindo do centro e dividindo todos os 6 lados ao meio.
- Você é uma daquelas pessoas que tem fome de conhecimento? Então siga o Beduka no Instagram para conteúdos diários!
E se for um prisma ou pirâmide de base hexagonal?
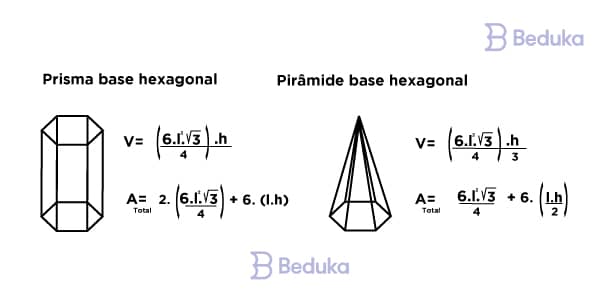
A figura hexágono é da geometria plana, mas pode servir de base para a formação de um prisma (um sólido da geometria espacial). Nesses casos, falamos do volume ou da área total de um sólido geométrico.
- Volume (V): medida da capacidade de um sólido geométrico. Usamos para medir quanto cabe dentro dele, ou seja, falamos dos corpos que possuem três dimensões (largura, altura e profundidade).
Para calcular o volume de um prisma qualquer, a fórmula é “área da base vezes altura”. Se for uma pirâmide, dividimos por 3. Assim:
V (pris) = b.h
e
V (pir) = b.h / 3
Em se tratando de um sólido com base hexagonal, basta encontrar a área do hexágono e multiplicar pela altura (h), substituindo nas fórmulas acima. Assim:
V (pris. hex) = (6 . l² . √3 / 4) . h
e
V (pir. hex) = (6 . l² . √3 / 4) . h / 3
- Área total (At): é dada pela soma de todas as faces da figura geométrica.
Se for um prisma de base hexagonal, teremos 2 áreas hexagonais + 6 áreas retangulares. Se for uma pirâmide de base hexagonal, teremos 1 área hexagonal + 6 áreas triangulares. Agora basta aplicar as fórmulas.
Em resumo, temos:
At (pris.hex) = 2 A(hex) + 6 A (ret)
e
At (pir.hex) = A(hex) + 6 A (t)
A importância dos hexágonos pelo mundo!
Você já tinha parado para pensar que as colméias, as nuvens de Saturno e as estruturas químicas da grafita e os cristais de gelo são todos em formato hexagonal? Pois é!
As formas geométricas estão presentes em diversas manifestações da natureza como animais e plantas. No caso das abelhas, por exemplo, isso permite ter uma visão angular muito ampla.
A presença dessa forma geométrica em animais, por exemplo, auxilia na ampla visão já que conseguem abarcar diversos ângulos de uma vez só.
Os cientistas não tem uma explicação para tudo, mas eu imagino que isso acontece porque ele é uma estrutura cheia de propriedades regulares, fazendo com que as coisas funcionem de forma eficiente e organizada!
E você, o que acha disso? Conta pra gente!
Gostou do nosso artigo sobre Hexágono? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet!





