O que é ponto, reta e plano? Conceitos e exemplos!

Ponto, reta e plano são os elementos básicos da Geometria. Eles não possuem uma definição formal, mas podemos identificá-los se conhecermos suas características e postulados. Superficialmente, dizemos que a reta é um conjunto de pontos assim como o plano é um conjunto de retas, mas é preciso entender as outras propriedades.

Neste artigo sobre Ponto, Reta e Plano, você encontrará:

1. Qual a definição de ponto, reta e plano
2. Como podemos indicá-los
3. Quais sãos suas propriedades e características (de cada um)
4. Diferença entre plano e espaço
5. Outros assuntos matemáticos que precisam dessa matéria

• Estudando para as provas? Conheça O melhor Simulado do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!

Qual a definição de espaço, ponto, reta e plano?

Ponto, reta, plano e espaço são noções da Geometria que não possuem uma definição sistemática (certinha). Podemos reconhecê-los por meio de suas características e postulados, além de precisarmos deles para formar todos os outros conceitos geométricos.

Esses elementos são a base da Geometria Plana, então são conhecidos como entes primitivos (as coisas que vieram primeiro).

A Geometria Plana também pode ser chamada de Euclidiana, pois foi o matemático grego Euclides quem a descobriu. Desde a época, os matemáticos notaram que não conseguimos definir de maneira formal esses elementos, pois os percebemos usando a nossa intuição.

Mesmo pela intuição, podemos confiar que esses elementos são verdadeiros porque, com base neles, formulamos outras definições verdadeiras. Além disso, elas vêm das características ou das consequências dessas ideias. 

A isso damos o nome de postulados ou axiomas. São algumas verdades que sustentam todo o sistema geométrico-matemático.

Essa foi apenas uma introdução, continue lendo esse artigo para entender as características importantes de cada um deles!

Como devemos indicar um ponto, uma reta e um plano?

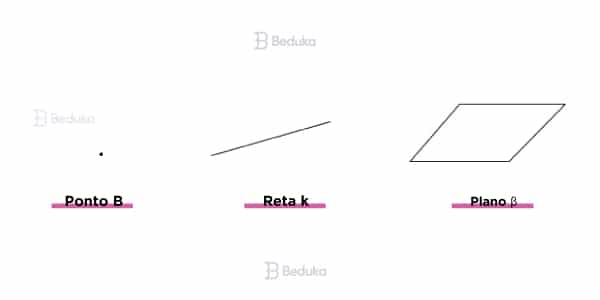
Para indicar, se referir ou representar um ponto, reta e plano; precisamos conhecer o símbolo usado para cada um deles:

• O ponto é representado por qualquer letra maiúscula do alfabeto latino (o normal, que usamos no dia a dia).
• A reta é indicada por qualquer letra minúscula do alfabeto latino.
• O plano é referido por alguma letra minúscula do alfabeto grego.

A seguir, vamos descrever os postulados de cada conceito (ponto, reta e plano) para você entender melhor o que são eles:

O que é o ponto? (características)

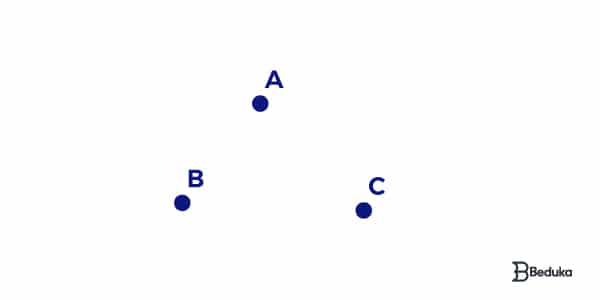
O ponto é o único ente geométrico que realmente não pode ser definido. O que sabemos sobre ele são suas características, ou seja, aquilo que podemos perceber e que os axiomas nos garantem:

• É a noção geométrica mais primitiva de todas.
• Não possui dimensão (adimensional) e nem formato.
• Usamos para indicar localização, pois são mais precisos (se fosse um triângulo, por exemplo, não saberíamos em qual parte da figura o local indicado se encontra).
• O ponto é dito como algo que “não tem partes”. 
• Ele é literalmente um pontinho, como o ponto final ou quando você faz um ponto com a caneta sobre uma folha.
• É representado por uma letra maiúscula latina.

O que é uma Reta? (Definição)

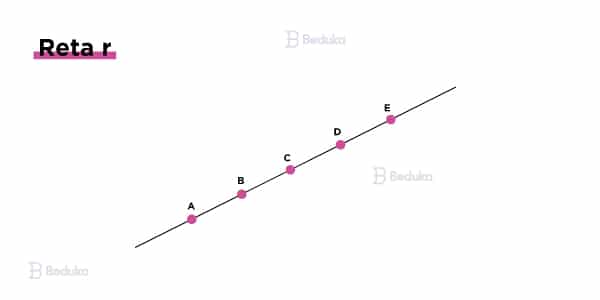
Apesar de não existir uma definição sistemática, podemos dizer que uma reta é um conjunto de pontos alinhados, ou seja, não fazem curvas. Outras características que nos ajudam a identificá-la são:

• É preciso, no mínimo, dois pontos para se traçar uma reta.
• Elas são infinitas nas duas direções (nas duas pontas), porque os pontos são infinitos e espalhados “por aí”.
• Uma reta não tem origem ou extremidade.
• Não conseguimos determinar o seu comprimento (é ilimitada).
• Os pontos que a compõe não são coincidentes, ou seja, não estão em um mesmo lugar (uns sobre os outros).
• Por isso, é possível medir a distância entre os pontos ou medir uma parte da reta.
• A reta possui apenas uma dimensão (unidimensional), porque os pontos são adimensionais, então não podemos medir sua altura ou largura. Só podemos medir o seu comprimento (distância).
• Cada reta é indicada por uma letra minúscula latina.
• Podemos dizer que é uma “linha” reta, sem curva.

Quando paramos para analisar partes das retas, podemos falar sobre os segmentos de retas (tem início e fim bem definidos) ou as semirretas (tem início mas segue infinito ao longo da reta).

Os segmentos são aqueles que compõem os lados ou arestas das figuras geométricas e são indicados assim: AB. Isso significa que o segmento começa no ponto A da reta e termina no ponto B.

As retas podem aparecer em 3 posições: horizontal, vertical ou inclinada.

Posição relativa entre retas

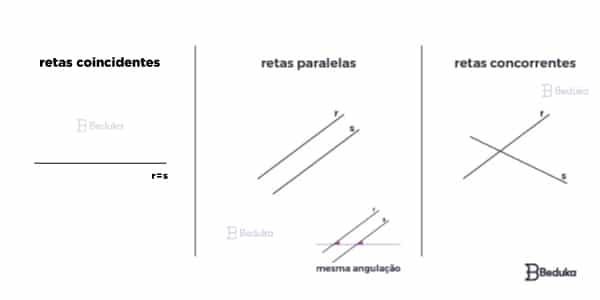
Quando estamos analisando diferentes retas ao mesmo tempo, dependendo da forma que elas se cruzam, podemos dar nomes a esses fenômenos:

• Retas paralelas: quando elas não possuem nenhum ponto em comum, estão perfeitamente alinhadas lado a lado. O símbolo usado para representar é: c // b , ou seja, a reta c é paralela a b.
• Retas concorrentes: quando as retas possuem um único ponto em comum, ou seja, se cruzam em um único lugar. Dependendo do ângulo que formam quando se cruzam, ainda podem ser classificadas em perpendiculares (formam ângulo de 90°) ou transversais (formam outros ângulos).
• Retas coincidentes: são retas que estão sobrepostas, ou seja, possuem todos os  pontos em comum. Nesse caso, elas são iguais.

O que é o Plano?

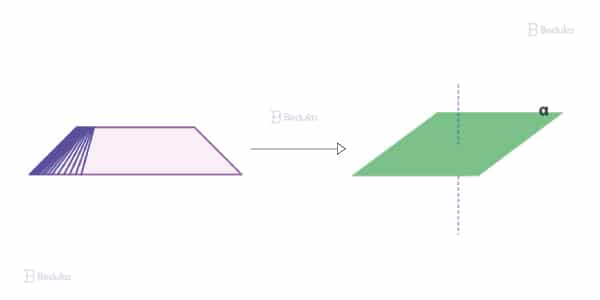
Dizemos que o plano é um conjunto de retas alinhadas, coladinhas umas nas outras. Pela consequência da definição da reta, podemos dizer que o plano também é um conjunto de pontos. 

A área formada por esse alinhamento de retas e pontos é uma superfície plana, então chamada de Plano. Outras características são:

• O plano é uma superfície reta, não faz curva.
• O plano é bidimensional (podemos medir sua altura e largura, como uma folha de papel).
• É possível desenhar figuras sobre o plano. 
• Um plano pode ser formado por 3 pontos não colineares (imagine um triângulo, ele é uma região plana com 3 vértices).
• Também pode ser formado por 1 reta mais um ponto fora dela.
• É representado por letras gregas minúsculas, como α, β, etc.
• Um plano pode ser formado por duas retas concorrentes ou paralelas distintas.

Alguns matemáticos, como Descartes, fizeram o esquema de planos com elementos destacados. Estamos falando daquele que tem 2 retas em sentidos diferentes e alguns de seus pontos são representados por números. 

É isso mesmo, estamos falando do Plano Cartesiano! É essencial saber seus elementos e como usá-lo, não deixe de ler o artigo!

Outros postulados importantes que envolvem ponto, reta e plano

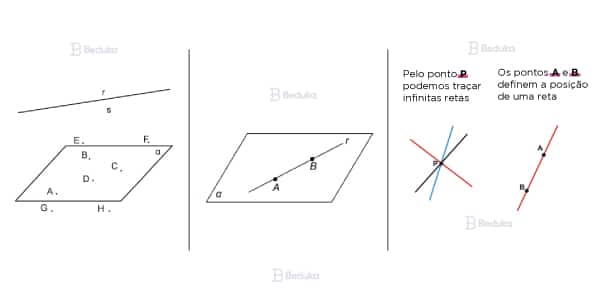
Agora que você já entendeu o que caracteriza cada um, podemos relacioná-los uns com os outros. Já falamos de postulados ao longo do texto até aqui, mas vamos acrescentar mais alguns que são importantes de gravar, pois te ajudam na hora de resolver exercícios:

“Por um único ponto no espaço, passam infinitas retas.” 

Isso significa que uma reta é formada por pontos não exclusivos. Ou seja, eu posso ter uma reta r que passa pelos pontos A e B, mas também ter uma reta s que passa pelos pontos A e C.

“Todo ponto que pertence a uma reta divide-a em duas semirretas, das quais o ponto é a origem.”

Esse postulado é explicado quando lembramos do conceito de semirreta (começa em um ponto definido e não tem fim, percorrendo o restante da reta).

“Existem infinitos pontos dentro e fora de uma reta.”

Quando analisamos toda a região ao redor desses entes, vemos que podemos tomar quantos pontos quisermos dentro de uma reta e outros tantos ficarão fora dela.

Como consequência disso e seguindo o mesmo raciocínio, podemos definir outros dois postulados:

“Existem infinitos pontos dentro e fora de um plano.” e “Existem infinitas retas dentro e fora de um plano”.

“Se dois pontos distintos de uma reta forem pontos de um plano, então a reta também é parte desse plano.”

Esse é chamado de postulado da inclusão. São aquelas afirmações lógicas que vamos deduzindo.

• Posição relativa entre retas e pontos

 Quando estamos analisando os pontos ao redor de uma reta, podemos dar nomes a esses fenômenos dependendo da forma que se relacionam:

→ Pontos pertencentes: o ponto está localizado sobre a reta ou é um dos que formam a reta.

→ Pontos que não pertencem: estão ao redor da reta, mas a reta não passa por eles.

É na Geometria Analítica que aprendemos a fazer os cálculos que medem essas distâncias!

Quais os símbolos que indicam pertencimento e contenção?

• Quando queremos dizer que um ponto pertence a uma reta ou uma reta pertence a um plano, usamos o símbolo ∈. Se for para afirmar que algo não pertence, usamos o ∉

Exemplo: “O ponto K pertence à reta s” seria indicado como “K ∈ s”.

• Se queremos dizer que um ponto/reta está contido em um plano, o símbolo usado é o ⊂. Quando não está contido, usamos o ⊄.

Exemplo: “A reta r está contida no plano β” seria indicado como “r ⊂ β”.

• Para dizer que um plano contém uma reta/ponto, o símbolo usado é o ⊃. Quando não contém, usamos o ⊅.

Exemplo: “O plano α não contém o ponto L” seria indicado como “α ⊅ L”.

Você é uma daquelas pessoas que tem fome de conhecimento? Então siga o Beduka no Instagram para conteúdos diários!

Qual a diferença entre Plano e Espaço?

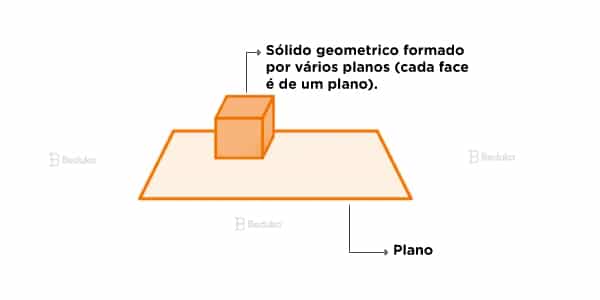
Chegamos ao nosso último conceito! Muitos estudantes confundem plano e espaço, mas a diferença é até simples: o espaço é o local geral, que engloba tudo o que conhecemos e todos os tipos de Geometria que estudamos até o Ensino Médio.

Assim como a reta é o alinhamento de pontos e o plano é o alinhamento de retas, dizemos que o espaço é formado pelo alinhamento de planos!

Sim, como você deve suspeitar, ele é infinito para todas as direções e contém todas as figuras geométricas planas e formas tridimensionais (sólidos da Geometria Espacial).

Como é formado por vários planos em diferentes sentidos, o espaço envolve a terceira dimensão (largura, altura e profundidade). Enquanto no plano só representamos quadrados, no espaço nós podemos representar cubos.

Gostou do nosso artigo sobre Ponto, Reta e Plano? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet!