A Combinação (C n,p) é um tipo de agrupamento da análise combinatória que calcula quantos subconjunto de “p” elementos podemos formar partindo de um conjunto inicial com “n” elementos. Nesse caso, a ordem das combinações não importa, pois trocá-la gera o mesmo resultado. Há 2 tipos de Combinações que possuem suas próprias fórmulas.
Ficou confuso?
Calma, nós vamos te explicar desde o início!
Neste texto sobre Combinação, você encontrará os tópicos abaixo. Clique em um deles para ir diretamente ao conteúdo:
- Introdução à Análise Combinatória.
- O que é Combinação?
- Características das Combinações.
- Símbolo das Combinações.
- Fórmula da Combinação Simples.
- Tipos de Combinação e quando usá-las.
- Combinação Simples + Exemplo de questão resolvida.
- Combinação Composta + Exemplo de questão resolvida.
- Diferença entre Permutação, Arranjo e Combinação.
- Curiosidade.
- Estudando para as provas? Conheça O melhor Simulado do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!
Introdução à Análise Combinatória
A Análise Combinatória é a área da Matemática que estuda as formas de resolver problemas com contagem de elementos ou possibilidades de algo ocorrer. Ela vai nos dizer quais as técnicas e métodos para cada tipo de situação.
O Princípio Fundamental da Contagem (PFC) e o Fatorial são contas que aprendemos a fazer desde o Ensino Fundamental, pois eles são a base da análise combinatória e seu raciocínio. Não deixe de ler antes de continuar!
Em outras situações, os cálculos tendem a se tornar complexos. Para facilitar o desenvolvimento das ideias, nós dividimos as técnicas de acordo com as situações. Elas podem ser um caso de Permutação, Arranjo ou Combinação.
O que é Combinação?
Combinação é a quantidade de grupos que podemos fazer com “p” elementos retirados de um conjunto de “n” elementos. Nessa contagem, buscamos identificar todos os subconjuntos com n elementos de um conjunto inicial p.
Quando escolhemos alguns elementos de um conjunto, podemos organizá-los em grupos menores. Neste caso, a ordem desses elementos dentro do grupo não interfere. Isso significa que trocar a posição dos elementos nos dá os mesmos resultados.
Exemplo
Vamos tomar como base um conjunto “n” formado por 4 elementos (José, Maria, Gabriel e Ana). Se nós queremos agrupar-los em subconjuntos de 2 elementos (2 a 2), teremos 6 resultados de combinações diferentes e possíveis:
José e Maria / José e Gabriel / José e Ana / Maria e Gabriel / Maria e Ana / Gabriel e Ana.
Cada uma dessas 6 duplas é uma combinação diferente dentre os 4 elementos do conjunto organizados em grupos de 2 elementos.
- São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!
Quais as Características da Combinação?
É importante notar que as Combinações levam em conta somente a natureza dos elementos. Vamos explicar:
Olhando as duplas acima, você é capaz de perceber que uma dupla feita por “Ana e João” é exatamente a mesma feita que “João e Ana”, porque envolve as mesmas pessoas.
O critério para organizar combinações é ter uma natureza diferente (ser pessoas, números ou cores diferentes). Por isso dizemos que, na Combinação, a ordem com que os elementos estão dispostos não importa.
É interessante saber que o ramo da genética na biologia utiliza combinações como ferramentas para estudar os possíveis genótipos e fenótipos dos seres. Para engenheiros da computação, o desenvolvimento de senhas e códigos também depende.
O estudo das combinações está mais presente no nosso dia a dia do que percebemos!
Qual o símbolo da Combinação?
O símbolo que representa a definição de Combinação é:
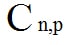
Lemos assim: “Combinação de n elementos, de p em p.”
Em que:
- n = número de elementos do conjunto inicial.
- p = número de elementos do subconjunto.
- C = quantidade de combinações possíveis nessas condições.
Isso é válido desde que n ≥ p, pois é impossível eu querer combinar 3 números em grupos de 4 algarismos, por exemplo.
Dessa forma, representamos o exemplo do primeiro tópico como C 4,2 = 6 (4 pessoas organizadas em duplas que resultam em 6 opções diferentes).
Qual a fórmula da Combinação Simples e Composta?

Você viu no tópico anterior que é trabalhoso ficar montando combinações manualmente. Imagina se a questão pedisse um C 40,3… Além de dar trabalho e poder fazer confusão, quanto mais elementos maior o tempo gasto.
Pensando justamente nas questões de vestibulares, há fórmulas que nos poupam tempo e trabalho! Basta substituir cada elemento na posição correta e resolver como uma equação normal.
Assim, não é necessário gastar tempo montando todas as combinações possíveis, basta aplicar a fórmula de Combinação Simples: C n,p = n! / p!(n – p)! Ela deve ser usada em situações em que a ordem não importa e seguindo a condição n ≥ p.
Para a Combinação Composta há outra fórmula. Falaremos sobre essas diferenças e daremos exemplos no próximo tópico!
Lembre-se:
- A exclamação (!) na frente do número/letra indica a operação de Fatorial.
- O espaço entre “p!” e o parênteses (no denominador), indica uma multiplicação.
Quais os tipos de combinações e quando usá-las?
Nós sempre usaremos a Combinação quando a questão não der importância à ordem. Ainda assim, existem várias situações diferentes que esse fator aparece. É daí que surgem os 2 tipos de Combinações: Simples ou Composta.
Vamos conhecê-los!
O que é uma Combinação Simples? [Exemplo]
A Combinação Simples é um tipo de agrupamento da análise combinatória em que a ordem não importa e não há repetição de elementos no conjunto inicial.
De uma maneira mais formal, a combinação simples pode ser definida como:
“Dados n elementos distintos, chama-se combinação desses n elementos tomados p a p (com p ≤ n) qualquer subconjunto formado por p elementos distintos, escolhidos entre os n.”
Exemplo
1) Em um congresso há 50 homens e 30 mulheres. Quantas comissões de 6 pessoas podemos formar, obedecendo a condição de que cada uma tenha 4 mulheres e 2 homens?
Solução
O primeiro passo é notar que trocar a ordem das pessoas que fazem parte de uma comissão não a torna diferente. Além disso, cada pessoa é um indivíduo, é único. Portanto, temos certeza que se trata de uma Combinação Simples.
O segundo passo é perceber que, no grupo de 6 membros, é preciso haver 4 mulheres e 2 homens. Isso nos mostra que faremos duas combinações diferentes (uma para cada sexo). Depois, basta multiplicar os resultados para saber a combinação total de comissões.
- Para homens:
C 50,2 = 50! / 2!(50-2)!
C 50,2 = 50.49.48! / 2!.48!
C 50,2 = 50.49 / 2.1
C 50,2 = 25.49
C 50,2 = 1225
- Para mulheres:
C 30,4 = 30! / 4!(30-4)!
C 30,4 = 30.29.28.27.26! / 4!.26!
C 30,4 = 30.29.28.27 / 4.3.2.1
C 30,4 = 10.29.7.27 / 2
C 30,4 = 27 405
- Comissões totais:
C30,4 . C50,2 =
27 405 . 1225 =
33 571 125 possibilidades de comissões.
- Atenção: Se no enunciado não houvesse a condição de 4 mulheres e 2 homens em cada subconjunto de 6, bastaria fazer um C 80,6 para achar as possibilidades.
Combinação Composta + Exemplos
A Combinação Composta, também chama de “com Repetição”, é um tipo de agrupamento da análise combinatória em que a ordem não importa e há a repetição de elementos no conjunto inicial.
Exemplo
1) Ângela foi à sorveteria para comprar um sorvete com quatro sabores. Chegando lá, viu que só tinha 3 disponíveis: chocolate, baunilha e morango. Quantas são as possibilidades que ela tem para montar um sorvete?
Solução
O primeiro passo é notar que se trata de uma combinação composta porque: a ordem dos sabores não interfere nas possibilidades e ela deverá repetir um sabor se quiser ter 4 bolas. Esse é um caso de combinação em que p > n.
Por causa disso, teremos de usar a fórmula própria:
C composta 3,4 = (3 + 4 – 1)! / 4! (3 – 1)!
C composta 3,4 = 6! / 4! . 2!
C composta 3,4 = 6.5.4! / 4! . 2.1
C composta 3,4 = 3.5
C composta 3,4 = 15 possibilidades.
Qual a diferença entre Permutação, Arranjo e Combinação?
Nós te dissemos que a análise combinatória é a área que estuda diferentes métodos para diferentes casos, sendo eles: Arranjo, Permutação e Combinação.
A essa altura, você já entendeu o que é Combinação: apenas a natureza importa, a ordem não.
Resumidamente, os Arranjos são agrupamentos em que a ordem importa, bem como a natureza. Imagine uma senha numérica: o número 23 é diferente do número 32, porque mesmo contendo os mesmos elementos (natureza), a ordem produz números distintos.
Já a Permutação é um caso específico de Arranjo. Nela, só a ordem importa (a natureza não). Isso porque o número de elementos do conjunto é igual ao número de elementos agrupados, ou seja, n = p.
Curiosidade
Você sabia que os Números Binomiais podem ser representados por Combinações?
É isso mesmo, esses temíveis números são expressos pela mesma fórmula que a Combinação Simples…
Se você entendeu esse artigo, com certeza é capaz de dar o próximo passo e enfrentar esse medo dos binomiais!
Gostou do nosso artigo sobre Combinação? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!






4 Comentários
otimo post, explicacao simples e funcional
Ficamos felizes que conseguimos te ajudar Gustavo.
Excelente. Poderia complementar informando como calcular a combinação de n elementos de p em p, com garantia g? Ex: Combinação de 6 elementos 4 a 4 “com garantia de 3”, ou seja, a menor quantidade de linhas da combinação resultante que atenda a garantia. Sabemos que a C6,4 = 15 => Isto é, escolhendo qualquer conjunto de 4 elementos dentre os 6, teremos pelo uma combinação com 4. Agora, e se a garantia for 3, quantas linhas dessa combinação serão necessárias para que pelo menos 1 tenha 3 dentre as 6? Já perguntei à vários professores e ninguém respondeu. Também não encontrei na internet. Grato.
Marcelus, ficamos felizes que tenha gostado do texto, mas sentimos em informar que também não temos resposta para sua questão. 🙁