Números Binomiais: o que são, importância e como usar!

Os Coeficientes ou Números Binomiais são formas algébricas de representar um valor. Ele é genericamente expressado por “n” sobre “p”, dentro de um parêntesis. Esse valor pode ser calculado desenvolvendo-se uma fórmula com fatorial, semelhante a da análise combinatória. Eles possuem propriedades e tipos, como o de Newton ou o de Pascal.

Neste texto sobre Números Binomiais, você encontrará os tópicos abaixo. 

Clique em um deles para ir diretamente ao conteúdo!

1. O que são Números Binomiais?
2. Elementos do Coeficiente Binomial.
3. Condição de Existência.
4. Como desenvolver um Coeficiente Binomial?
5. Para que servem? (quando usar).
6. Propriedades dos Coeficientes Binomiais (como usar).
7. Binômios particulares.
8. Binomiais complementares.
9. Relação de Stifel.
10. Triângulo de Pascal.
11. O Binômio de Newton.

• Estudando para as provas? Conheça O melhor Simulado do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!

O que são Números Binomiais?

Os Números Binomiais são aqueles representados por dois termos sobrepostos e entre parênteses. Também conhecidos como Coeficientes Binomiais, eles são apenas uma representação algébrica para indicar valores.

Pode não fazer sentido agora, mas vamos te explicar, em um tópico a frente, qual a sua importância. 

Antes disso, precisamos conhecer os elementos e o símbolo de um Coeficiente Binomial. 

• São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!

Elementos do Coeficiente Binomial

Número Binomiais são genericamente representados por:

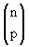
Lemos esse número binomial da seguinte forma: “n sobre p”. 

Essas letras foram escolhidas aleatoriamente, apenas para mostrar que podem ser substituídas por quaisquer valores. Elas são incógnitas.

É como se fosse uma fração com numerador (n) e denominador (p). Porém, não usamos o traço entre eles, justamente para diferenciar. O coeficiente binomial não equivale a uma simples divisão.

Condição de existência

Quando estudamos as equações e funções da álgebra, sempre falamos em condição de existência. 

Ela é apenas uma informação que indica quais valores numéricos aquela incógnita (nesse caso, “n” e “p”) podem assumir para que esse cálculo seja válido.

A condição de existência de um Coeficiente Binomial é:

(n, p ∈ N e n ≥ p)

Em outras palavras, quer dizer duas coisas:

• “n” e “p” só podem assumir valores que pertencem ao conjunto dos números naturais.
• “n” deve ser um número maior ou igual a “p”.

Como desenvolver um Coeficiente Binomial?

Você deve estar se perguntando: se isso é a representação de um número, como saber seu valor? 

Os matemáticos que inventaram essa representação já deram a fórmula para calculá-lo. Por definição, sabemos que:

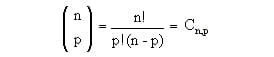
Se você já estudou análise combinatória, essa fórmula vai te parecer familiar, pois é usada na Combinação. Daí é que surge a possibilidade de representar com o “C n,p”.

Para aqueles que ainda não estudaram, vamos explicar: 

A exclamação (!) significa que devemos realizar a operação do fatorial desse número. Então, para calcular o valor de um número binomial, devemos:

Realizar o fatorial do numerador (n!) dividido pela multiplicação entre o fatorial do denominador (p!) e o fatorial da subtração entre numerador e denominador ([n – p]!).

Para que servem os Números Binomiais?

Pode parecer complicado para nós, que só usamos números normais no dia a dia, qual o sentido de usar essas representações cheias de fórmulas e contas. 

Ainda assim, os números binomiais são uma ferramenta que acelerou os avanços na matemática e na engenharia, porque facilitaram o cálculo de produtos notáveis (fatoração de polinômios).

Um binômio é uma expressão matemática composta por dois termos que se subtraem ou somam. Veja os exemplos:

• (4x + 2y)
• (x – 3y)
• (2x + y)

Note que eles não são uma equação que nos permite calcular algo, pois não existe um sinal de igual (=). Ele é um valor abstrato.

Na vida escolar, nós lidamos com esse tipo de número quando estamos resolvendo expressões polinomiais e temos que desenvolver os binômios, por estarem sob uma potência. 

Aí usamos as regrinhas de produtos notáveis:

• (n+p)⁰= 1
• (n+p)¹= (n+p)
• (n+p)²= n² + 2np + p²
• (n+p)³= n³ + 3n²p + 3np³ + p³

Lembrou? No Ensino Fundamental, nós só aprendemos a resolver binômios com potências para os expoentes menores ou iguais a 3.

Porém, os binômios de Newton (sim, o cientista) servem justamente para as situações em que precisamos resolver binômios elevados a expoentes maiores ou iguais a 4.

Concluímos que o coeficiente binomial é importante para o que vem depois da matemática básica e, graças a ele, os físicos, químicos e matemáticos puderam evoluir nas ciências.

• Agora que já entendemos o que é esse número, como descobrir seu valor e qual sua aplicação, vamos trabalhar as propriedades dele:

Propriedades dos Números Binomiais

Toda vez que falamos em “propriedades” em algum assunto matemático, estamos nos referindo a instruções. Elas são regrinhas que nos indicam qual o procedimento que faremos ao se deparar com um contexto específico (neste caso, que envolva binômios).

Vamos conhecer as propriedades dos coeficientes binomiais:

Binômios particulares

Existem 3 casos particulares em que não é necessário fazer o desenvolvimento usando a fórmula. A gente consegue bater o olho e saber o resultado, porque ele sempre será o mesmo.

Ainda assim, aqui nós vamos te apresentar o desenvolvimento, apenas para provar que é verdade. Mas, de agora em diante, tente decorar essas 3 relações para não ter esse trabalhão todo:

Binomiais Complementares

Dois coeficientes binomiais serão do tipo complementares se seus numeradores forem iguais e a soma de seus denominadores for igual ao numerador. 

É importante saber dessa definição, pois os valores de binômios complementares são iguais.

Exemplo

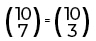
Para saber se eles são complementares mesmo, vamos fazer:

1° binômio: n = 10 e p = 7

2° binômio: n = 10 e p = 3

De fato, seus numeradores são iguais (valem 10) e a soma de seus numeradores (7 + 3) é igual ao numerador (10).

Agora, podemos afirmar que o valor desses binômios serão os mesmos, por isso foram escritos em uma equação (sinal de = entre eles) verdadeira. 

Desenvolvendo:

1° binômio:   10! / 7! (10 – 7)!   =   10! / 7! . 3!   =  120

2° binômio:   10! / 3! (10 – 3)!   =   10! / 3! . 7!   =   120

Relação de Stifel

Essa propriedade tem esse nome por causa da homenagem ao matemático alemão que a descobriu, Michael Stifel. Ela diz que: 

“Ao somar dois binômios, se o primeiro possui um denominador que é antecessor do denominador do segundo, o resultado será um binômio com o denominador do segundo, mas com o sucesso de seu numerador.”

Parece confuso? Veja o esquema que representa essa propriedade para facilitar:

Triângulo de Pascal e os números binomiais

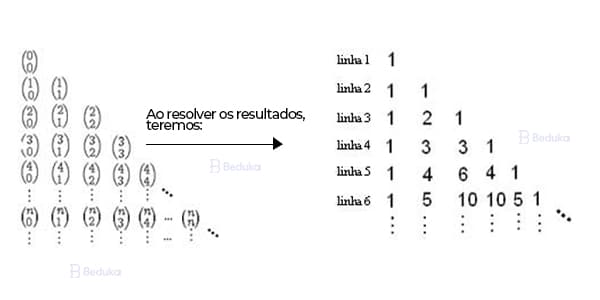
Os coeficientes binomiais podem ser organizados, em ordem crescente, em um formato de triângulo retângulo. A esse fenômeno chamamos de Triângulo de Pascal ou Tartaglia.

Organizá-los dessa forma nos permite observar uma série de propriedades internas, que podem ajudar na hora de resolver questões de progressão numérica. Na imagem acima, você pode ver como fica esse triângulo.

Note que a ordem adotada faz com que os binômios de mesmo numerador fiquem em uma mesma linha (horizontal). Já os binômios de mesmo numerador ficam em uma mesma coluna (vertical).

Resolvendo esses binômios no triângulo, teremos os resultados apresentados. Você consegue observar o padrão? É incrível e há uma utilidade nisso tudo:

Quando somamos os elementos de uma mesma linha, os resultados nos dão uma progressão de base 2 (vem dos binômios):

1° Linha = 1 (equivale a 2⁰)

2° Linha = 1 + 1 = 2 (equivale a 2¹)

3° Linha = 1 + 2 + 1 = 4 (equivale a 2²)

4° Linha = 1 + 3 + 3 + 1 = 8 (equivale a 2³)

5° Linha = 1 + 4 + 6 + 4 + 1 = 16 (equivale a 2⁴)

E assim por diante…

O Binômio de Newton

O famoso cientista Isaac Newton, além de tudo, ainda desenvolveu uma fórmula usando binômios. 

O binômio de Newton é uma fórmula que nos permite calcular um termo do binômio sem precisar desenvolvê-lo todo. Em outras palavras, calculamos diretamente o termo que estamos procurando.

Lembra que, no início do texto, nós desenvolvemos alguns binômios que estavam elevados a expoentes de 0 a 3? 

Pois é, logo depois falamos que havia uma fórmula, usando coeficientes ou números binomiais, que nos permite calcular os de 4 para cima.

Se você voltar naquele tópico e reparar o resultado dos desenvolvimento, verá que existe um padrão. Newton foi o primeiro a perceber essa relação:

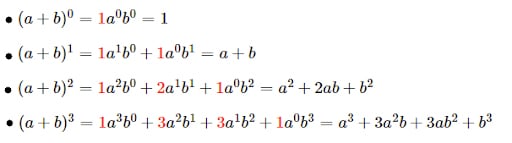
Logo acima, nós também vimos o Triângulo de Pascal.

Perceba: cada termo do desenvolvimento do produto notável elevado a qualquer número (a+b)ⁿ, associa-se a um binomial no triângulo de pascal.

Por causa disso, podemos dizer que o desenvolvimento de um produto notável pode ser representado assim:

Gostou do nosso artigo sobre Números Binomiais? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.

Experimente agora!