O Baricentro de um triângulo é o ponto (G) em que todas as medianas se cruzam. Ele pode ser chamado de centróide, centro de massa ou centro de gravidade; por que é o ponto de equilíbrio da figura plana. Ele também divide as medianas em uma razão de 2:1 e há fórmulas específicas da Geometria Analítica para calculá-lo!
Neste texto sobre Baricentro, você encontrará os tópicos abaixo.
Clique em um deles para ir diretamente à parte que você deseja!
- O que é Baricentro do triângulo?
- Qual sua importância e para que serve.
- Introdução: conceitos básicos da Geometria Analítica.
- O que é Ponto Médio e Mediana.
- Sistema de Coordenadas e Plano Cartesiano.
- Como calcular o Baricentro? (3 passos + fórmula).
- De onde veio a fórmula?
- Exemplos de questões resolvidas.
- Estudando para as provas? Conheça O melhor Simulado do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!
O que é o Baricentro do Triângulo?
O Baricentro de um triângulo é o ponto (G) no qual todas as três medianas se cruzam. Ele sempre estará presente, independente do tipo de triângulo que analisamos.
Ele também pode ser chamado de centróide, centro de massa ou centro de gravidade; porque é o ponto de equilíbrio. Isso significa que, se o dedo embaixo de uma figura plana triangular com a ponta bem no baricentro, a figura não cai.
Outra característica do Baricentro é dividir as medianas em duas partes numa razão de 2:1 (uma parte é o dobro da outra). Assim, o maior segmento é que tem sua extremidade no vértice do triângulo.
Pareceu abstrato demais? Calma! Esse foi só o conceito.
Nos próximos tópicos, nós vamos te dar a explicação completa com imagens! Antes, vamos apenas entender o porquê disso ser importante.
Qual a importância do centróide e sua aplicação?
O baricentro foi descoberto na Geometria Matemática, mas sua aplicação se dá na Física, na Arquitetura, na Engenharia e muitas outras áreas presentes no nosso dia a dia.
Ele é o ponto onde a força da gravidade atua em um corpo, então é nele que podemos equilibrar as forças de atração. Graças a esse conceito, é que as construções de diversos formatos se mantêm em pé, foram criados foguetes e trajes espaciais, máquinas, etc.
Além disso, os triângulos e os baricentros são queridinhos da Geometria Analítica, matéria que cai nos vestibulares e no Enem.
Os assuntos que aparecem relacionados aos triângulos são relações métricas, tipos e semelhanças. Mas, hoje, focaremos no conceito de baricentro e na fórmula de suas coordenadas.
Introdução: conceitos básicos da Geometria Analítica
A Geometria é a área da Matemática que estuda as figuras, formas e suas características. Existem três tipos: Plana (figuras 2D), Espacial (figuras 3D) e a Analítica (medidas e coordenadas).
No estudo analítico dos triângulos, buscamos conhecer as coordenadas dos seus vértices. Com isso, será possível determinar qual é o tipo de triângulo, qual a sua área, outras medidas internas e onde está seu baricentro.
Por isso, vamos relembrar como funciona o sistema de coordenadas e o que é mediana. Logo depois, mostraremos a fórmula do Baricentro e um exemplo resolvido!
O que é Ponto Médio e Mediana?

Na geometria plana existem dois conceitos muito importantes, ponto médio e mediana. Vamos entender a definição de cada um deles, que formarão a ideia do Baricentro:
- Ponto Médio: um ponto que divide um segmento de reta em duas partes iguais. Em outras palavras, esse ponto divide ao meio cada lado do triângulo.
- Mediana: a mediana é o segmento de reta que liga um vértice do triângulo ao ponto médio oposto a ele.
Só por essas definições já conseguimos deduzir que todo triângulo, independente de seu formato, possui três pontos médios e três medianas.
Para facilitar, observe a imagem acima. Nela:
- Os vértices do triângulo são “A,B,C”.
- O ponto “M” é ponto médio do lado “AB”
- O ponto “N” é ponto médio do lado “AC”
- O ponto “O” é ponto médio do lado “BC”.
- Os riscos nos lados indicam que se dividem em segmentos iguais.
- A reta “r” é mediana que parte do vértice “C” e chega ao ponto médio oposto “M”
- A reta “q” é mediana que parte do vértice “A” e chega ao ponto médio oposto “O”
- A reta “s” é mediana que parte do vértice “B” e chega ao ponto médio oposto “N”.
- O ponto “G” é o baricentro, pois é onde as três medianas se cruzam.
Sistema de coordenadas e Plano Cartesiano
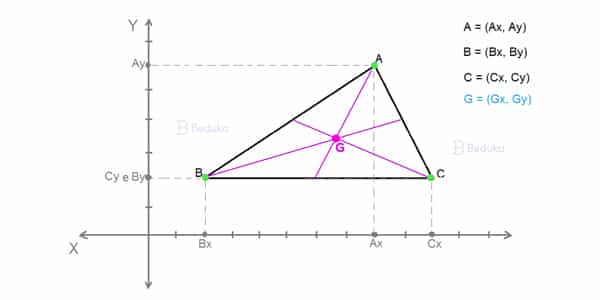
O Plano Cartesiano é uma ferramenta desenhada. Ele possui duas dimensões (altura e largura) marcadas com duas retas cheias de números. Ele é usado para localizar elementos em um espaço.
Imagine um tabuleiro de batalha naval ou de xadrez. Eles são malhas quadriculadas que nos permitem localizar algo quando temos duas referências (uma vertical, outra horizontal). Também é assim que o plano funciona.
A reta x possui números para marcar os pontos horizontais (abcissas) e a reta y tem números que marcam os pontos verticais (ordenadas). A partir disso criou-se o Sistema de Coordenas, a maneira de representar um ponto usando duas informações: (x,y).
Portanto, ao representar um triângulo no plano, nós podemos determinar as fórmulas e as coordenadas do Baricentro.
- São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!
Como se calcula o Baricentro? (3 passos)
Para calcular o baricentro de um triângulo, usamos uma fórmula da geometria analítica:
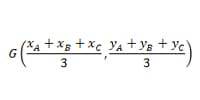
São necessários três passos:
- 1° Passo: devemos determinar os pares ordenados de cada vértice do triângulo e o do baricentro: (Ax, Ay), (Bx, By), (Cx, Cy) e (Gx, Gy).
- 2° Passo: depois, substituímos os valores que foram dados no enunciado da questão ou que conseguimos enxergar no plano, por meio da reta numérica.
- 3° Passo: por fim, aplicamos todos os números na fórmula, que se tornará uma equação de primeiro grau. Basta resolver a equação normalmente e encontraremos as coordenadas do baricentro.
Se for preciso, voltar na imagem do tópico anterior para enxergar esses pontos no plano cartesiano. Mas fique tranquilo, vamos te explicar um detalhe importante agora:
De onde veio a fórmula do centro de massa?
Você deve estar se perguntando que fórmula mais feia é essa! Por incrível que pareça, ela é mais simples do que imaginamos. Se você entender o raciocínio que tem por trás dela, não será uma mera questão de decorar. Vamos lá:
Anteriormente, vimos que o ponto médio divide um lado do triângulo ao meio, em dois segmentos iguais, não é? Pela lógica, se queremos saber sua localização, basta somar os valores dos vértices do lado em que ele está e dividir por dois.
Mas é preciso fazer duas operações, uma para os valores horizontais (x) e outra para os verticais (y), pois um vértice é dado por um par de coordenadas. É com base nesse raciocínio que surgiu a fórmula do baricentro.
Ele é formado pelo encontro das medianas do triângulo, dividindo-o em 3 partes de iguais pesos. Por isso, para descobrir o par ordenado do Baricentro, basta somar os valores horizontais de cada vértice e dividir por três. Depois, faça o mesmo com os valores verticais.
Exemplos de exercício resolvido sobre Baricentro
Questão 1) Determine as coordenadas do baricentro de um triângulo que possui vértices A(3, 8), B(6, 4) e C(3, 3).
Solução: O baricentro será determinado pelo par (Gx, Gy). Você pode jogar todos os valores dados na fórmula e resolver normalmente, mas aqui nós vamos fazer tudo separado para não confundir.
Primeiro, vamos calcular qual será o valor de Gx. Para isso, somamos todos os valores “x” dos vértices e os dividimos por 3:
Gx = (Ax + Bx + Cx) / 3
Gx = (3 + 6 + 3) / 3
Gx = 12 / 3
Gx = 4
Agora, vamos calcular o valor de Gy. Para isso, somamos todos os valores “y” dos vértices e os dividimos por 3:
Gy = (Ay + By + Cy) / 3
Gy = (8 + 4 + 3) / 3
Gy = 15 / 3
Gy = 5
Portanto, concluímos que a localização do baricentro será dada pelo par G(4,5).
Questão 2) João observou que o triângulo de uma figura estava com o valor do vértice B apagado. Mas ele conseguiu ler que as coordenadas do baricentro eram G(3, 4) e que os outros dois vértices eram A(2, 6) e C(2, 2). Ele era muito curioso e resolveu calcular qual seria a coordenada de B. Qual foi o valor corretamente encontrado por João?
Solução: a fórmula que usamos para descobrir o baricentro poderá ser usada aqui também.
Isso acontece porque ela funciona como uma equação, ou seja, foram dados três valores e iremos descobrir o quarto. Basta substituir cada coisa corretamente em seu lugar e realizar as operações.
Vamos começar descobrindo a coordenada Bx:
Gx = (Ax + Bx + Cx) / 3
3 = (2 + Bx + 2) / 3
3 . 3 = 4 + Bx
9 = Bx + 4
9 – 4 = Bx
Bx = 5
Agora, só precisamos de fazer o mesmo com a coordenada By:
Gy = (Ay + By + Cy) / 3
4 = (6 + By + 2) / 3
4 . 3 = 8 + By
12 = By + 8
12 – 8 = By
By = 4
João descobriu que o vértice B tem coordenadas B(5, 4).
Gostou do nosso artigo sobre Baricentro? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!






2 Comentários
Um dos site mas explicativos que já encontrei❤
Muito obrigado, Kaique! Conte conosco sempre!