6 exercícios de fração com gabarito para melhorar seu raciocínio. Responda agora!

Você sabia que o tracinho da fração significa divisão? Pois é,trata-se apenas uma outra forma de representar que um objeto foi dividido em partes iguais.

Esse é um dos conceitos mais básicos da matemática, mas acaba causando confusão entre os estudantes. Porém, com uma boa explicação e a prática de exercícios de comparação de frações, o assunto pode ser dominado facilmente.

Neste artigo, apresentaremos um resumo seguido de exercícios sobre fração justamente para te ajudar. Independentemente do seu nível atual de conhecimento, eles te ajudarão a testar seu conhecimento. Vamos começar!

Clique em um dos tópicos para ir direto ao conteúdo da sua escolha:

• O que é uma fração?
• Quais são os elementos de uma fração?
• Quais são os tipos de fração?
• Como fazer operações com fração?
• Lista de exercícios de Fração!
• Respostas das questões sobre Fração.

Esse assunto cai muito no Enem. E você está a poucos cliques de baixar o nosso Plano de Estudos para te guiar nesse jornada rumo à aprovação!

O que é fração?

Antes de resolver os exercícios de comparação de frações, você precisa conhecê-las né! Então vamos explicar brevemente só para refrescar a memória:

Fração é apenas uma forma de representar números que indicam uma divisão. Inclusive, usamos a fração especificamente quando queremos falar de um elemento que foi divido em partes iguais.

Talvez seja difícil imaginar isso, então vamos ver um exemplo em uma situação cotidiana:

Exemplos de frações no dia a dia

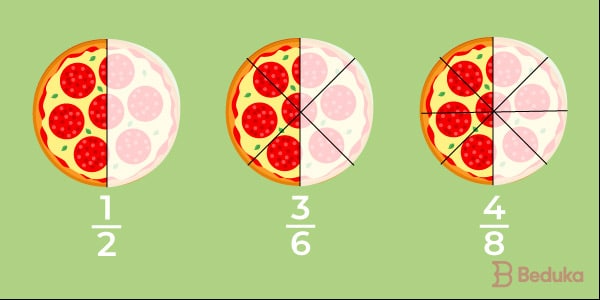
Imagina que você vai a uma pizzaria e recebe aquela pizza bem redonda. Aí você a corta em duas metades iguais. Em termos matemáticos, cada uma dessas metades é vista como uma parte das duas que haviam, ou seja, um meio (1/2). 

Só que você não estava sozinho. Tinha mais 7 amigos e cada um cortou um pedaço igual de pizza para sí. Sendo assim, na visão matemática, cada um comeu um oitavo (1/8) da pizza que antes era inteira (8/8).

Mas, agora vamos supor que um dos seus amigos não gosta de pizza, então ele dá o pedaço pedaço dele pra você. Você comeu dois pedaços do inteiro dividido em oito partes. Logo, você comeu dois oitavos (2/8).

Viu? Não é tão difícil quanto parece!

Quais são os elementos da fração?

Pelo exemplo aí de cima você já entendeu que, na fração, o total fica no número de baixo e a parte escolhida fica no número de cima.

Só tem um porém: nos textos de internet é difícil escrever um número em cima do outro, então escrevemos em linha reta. Aí o número à esquerda da barra é o número de cima, quanto o número à direita é o de baixo. Então, 2/8 é o mesmo que 2 dividido por 8 em pé.

E você sabia que esses números tem nomes? Eles são justamente os dois elementos da fração: 

• Numerador: é o dividendo, número que será dividido e que representa a parte. Comumente conhecido como “o número de cima”.
• Denominador: é o divisor, número que representa o todo e que vai dividir a parte. Ele representa a quantidade total de partes em que o numerador será dividido. Comumente conhecido como “o número de baixo”.

O numerador também é conhecido como o número que vai te fazer passar raiva… Continue lendo para entender o porquê!

Quais são os tipos de fração?

Há inúmeros tipos de fração e nós até já fizemos um artigo completo sobre Frações para você aprender toda a parte teórica.

Como este aqui é apenas um resumo para fazer os exercícios de fração, focaremos nos 5 tipos principais:

Fração Própria

É toda fração em que o numerador é menor que o denominador. Como consequência, sempre que você fizer uma divisão o resultado será menor que 1.

Imagine que numa caixa de bombom vieram 5 deles, mas 10 pessoas irão comer. Então cada bom bom terá de ser repartido igualmente para que todos comam, e ninguém vai comer um bombom inteiro sozinho.

Exemplos: 1/8 = 0,125 2/10 = 0,2 3/4 = 0,75

Todas as frações próprias resultam em números decimais. Ah, também é importante saber transformar frações em números decimais. Não deixe de ler esse artigo!

Fração imprópria

Pelo nome já dá para imaginar que essa é o contrário da de cima. Ou seja… a fração imprópria é uma fração em que o numerador é maior que o denominador, por isso tem um resultado maior que 1.

Lembra da caixa de bombom? É como se essa mesma caixa com 5 bombons fosse divida para 3 pessoas igualmente. Cada uma delas vai comer um bombom inteiro mais um pedacinho incompleto de outro.

Exemplos: 10/6 = 1,67 20/8 = 2,5

Se você estiver estranhando o termo “número inteiro”, precisa ler nosso artigo sobre conjuntos numéricos!

Fração aparente

Essas são as queridinhas, porque resultam em números inteiros, ou seja, dão resultados exatos, são divisões sem resto.

Ainda no caso da caixa de bom bom com 5 deles, seria o mesmo que pegar essa caixa e dividir para 5 pessoas. Cada uma delas receberia exatamente um, nem mais, nem menos. Também daria certo se fosse uma caixa grande com 10 bombons para 5 pessoas, cada uma receberia exatamente 2.

• Se você prestou atenção, já percebeu que uma fração aparente pode ser também imprópria. 10/2 é imprópria porque o numerador é maior que o denominador e continua sendo aparente porque o resultado é um número exato!

Já uma fração própria nunca poderá ser aparente. Isso porque elas possuem o denominador menor que o numerador, portanto, nunca poderão dar resultados exatos. 

Você sabia que também dá para transformar frações em porcentagens? Clique para ler nosso artigo explicando tudinho.

Fração equivalente

Esse tipo aqui é mais uma dica, não tem a ver com os elementos da fração. É que algumas frações podem ser reduzidas ou simplificadas.

Por exemplo, se olharmos a fração 5/15 , vemos claramente que o numerador e o denominador são divisíveis por 5. Quando dividimos os dois termos pelo mesmo número, obtemos a fração 1/3.

A prova de que podemos fazer isso é que o resultado de 5/15 e de 1/3 é o mesmo decimal: 0,33. Por isso, dizemos que são frações equivalentes.

Fração mista

Por último, a fração mista. Dos quatro tipos principais, esse é o mais complicado porque junta uma fração com uma parte inteira.

Exemplo: 2 3/6 (dois inteiros e três sextos)

Isso significa que nós temos dois elementos inteiros (6/6) + (6/6) e um terceiro que não se completou (3/6).

Isso equivale ao número 2,5 (dois inteiros e metade), que também pode ser representado pela fração 25/10. Simplificando, temos mais outra forma de representar que é 5/2. Viu? Diferentes jeitos de representar uma mesma coisa!

Existe uma fórmula que vai agilizar sua vida:

Denominador x número inteiro + numerador

Você pode simplesmente fazer o que dissemos agorinha em cima e conseguirá transformar uma fração mista em uma fração comum e equivalente: 15/6.

Como fazer operações com fração?

Você já conhece as frações, então está na hora de aplicá-las. Acompanhe com atenção para não errar na hora dos exercícios de fração. 

Soma de frações de mesmo denominador

Quando queremos somar duas frações e o denominador é o mesmo, só precisamos somar os numeradores e manter o denominador para ter o resultado.

Exemplo: 2/8 + 3/8 = 5/8

Mas se prepare porque isso quase nunca acontece em vestibulares. O caso mais comum é o que vamos mostrar agora:

Soma de frações com denominador diferente

Quando falamos que o denominador te faria passar raiva, não era brincadeira. É que não tem como somar frações com denominadores diferentes. Nesses casos, a primeira coisa a fazer é torná-los iguais.

Exemplo: 2/3 + 1/2 = ?

O Primeiro passo é descobrir o MMC (Mínimo Múltiplo Comum) desses denominadores. No caso de 3 e 2 o MMC é 6, esse será o novo denominador.

E tem mais: na matemática, não podemos mudar alguma coisa sem mudar outra. Se o denominador mudou, temos que mudar o numerador.

Para descobrir os novos numeradores, teremos que fazer as seguintes operações: 

• 6 (novo denominador) : 3 (antigo denominador) x 2 (antigo numerador) = 4 (novo numerador)
• 6 (novo denominador) : 2 (antigo denominador ) x 1 (antigo numerador) = 3 (novo numerador)

Assim, nós temos duas frações novas e com denominadores iguais: 4/6 e 3/6.

Agora sim podemos somar as frações, conservando o denominador e somando os numeradores.
4/6 + 3/6 = 7/6

Subtração de frações

A subtração funciona com a mesma lógica da adição. Em caso de denominadores iguais, basta subtrair um numerador do outro e manter o denominador.

Se os denominadores forem diferentes, você vai ter que fazer todo o processo de transformar as duas frações para só então subtraí-las.

Multiplicação de Frações

A multiplicação vai te deixar muito feliz, porque é como uma multiplicação normal.

Você multiplica o que está em cima pelo que está em cima. Depois multiplica o que está embaixo pelo que está embaixo. Pronto, está feito.

Exemplo: 3/4 x 5/2 = 15/8

Divisão de frações

Ufa, você não precisa mais se preocupar com denominadores. Para dividir uma fração por outra basta conservar a primeira e multiplicar pelo inverso da segunda. 

Exemplo: 1/2 : 3/4 = 1/2 x 4/3 = 4/6

Comparações de frações

Se eu te pedir para comparar 6/2 e 4/1, provavelmente você falaria que a primeira fração é maior.

Mas… é o contrário! Quando comparamos o tamanho das frações, as aparências enganam.

É porque as frações são divisões, então quanto maior for o número de baixo, menor o resultado final.

6/2 = 3 enquanto 4/1 = 4.

Viu? A segunda fração é maior no final das contas.

Exercícios de Fração

Bom, nós te ensinamos o que é fração e agora você pode fazer os exercícios de fração.

Só saiba que esse assunto é muito importante para o Enem, então capricha! E você pode treinar especificamente para essa prova com o nosso Simulado online e gratuito.

Agora vamos lá:

Questão 1 – (UFMG-2009)

Paula comprou dois potes de sorvete, ambos com a mesma quantidade do produto.

Um dos potes continha quantidades iguais dos sabores chocolate, creme e morango; e o outro, quantidades iguais dos sabores chocolate e baunilha.

Então, é CORRETO afirmar que, nessa compra, a fração correspondente à quantidade de sorvete do sabor chocolate foi:

a) 2/5.

b) 3/5.

c) 5/12.

d) 5/6.

Questão 2 – (Unesp-1994)

Duas empreiteiras farão conjuntamente a pavimentação de uma estrada, cada uma trabalhando a partir de uma das extremidades. Se uma delas pavimentar 2/5 da estrada e a outra os 81 km restantes, a extensão dessa estrada é de:

a) 125 km.

b) 135 km.

c) 142 km.

d) 145 km.

e) 160 km.

Questão 3 – (UECE-2009)

Uma peça de tecido, após a lavagem, perdeu 1/10 de seu comprimento e ficou medindo 36 metros. Nessas condições, o comprimento, em metros, da peça antes da lavagem era igual a:

a) 39,6 metros.

b) 40 metros.

c) 41,3 metros.

d) 42 metros.

e) 42,8 metros.

• Boa! Estamos na metade dos exercícios de comparação de frações.

Questão 4 – (ETEC/SP-2009)

Tradicionalmente, os paulistas costumam comer pizza nos finais de semana. A família de João, composta por ele, sua esposa e seus filhos, comprou uma pizza tamanho gigante cortada em 20 pedaços iguais. Sabe-se que João comeu 3/12 e sua esposa comeu 2/5 e sobraram N pedaços para seus filhos. O valor de N é?

a) 7.

b) 8.

c) 9.

d) 10.

e) 11.

Questão 5 – (Enem-2011)

O pantanal é um dos mais valiosos patrimônios naturais do Brasil. É a maior área úmida continental do planeta – com aproximadamente 210 mil km2, sendo 140 mil km2 em território brasileiro, cobrindo parte dos estados de Mato Grosso e Mato Grosso do Sul. As chuvas fortes são comuns nessa região. O equilíbrio desse ecossistema depende, basicamente, do fluxo de entrada e saída de enchentes. As cheias chegam a cobrir até 2/3 da área pantaneira. Durante o período chuvoso, a área alagada pelas enchentes pode chegar a um valor aproximado de:

a) 91,3 mil km2.

b) 93,3 mil km2.

c) 140 mil km2.

d) 152,1 mil km2.

e) 233,3 mil km2.

Questão 6 – (Enem-2017)

Em uma cantina, o sucesso de vendas no verão são sucos preparados à base de polpa de frutas. Um dos sucos mais vendidos é o de morango com acerola, que é preparado com 2/3 de polpa de morango e 1/3 de polpa de acerola.

Para o comerciante, as polpas são vendidas em embalagens de igual volume. Atualmente, a embalagem da polpa de morango custa R$ 18,00 e a de acerola, R$ 14,70. Porém, está prevista uma alta no preço da embalagem da polpa de acerola no próximo mês, passando a custar R$ 15,30.

Para não aumentar o preço do suco, o comerciante negociou com o fornecedor uma redução no preço da embalagem da polpa de morango.

A redução, em real, no preço da embalagem da polpa de morango deverá ser de

a) 1,20.

b) 0,90.

c) 0,60.

d) 0,40.

e) 0,30.

• Parabéns! Você terminou os exercícios de fração e pode conferir o gabarito aqui embaixo.

Respostas dos exercícios sobre fração

Exercício resolvido da questão 1 –

Alternativa correta: c) 5/12.

Exercício resolvido da questão 2 –

Alternativa correta: b) 135 km.

Exercício resolvido da questão 3 –

Alternativa correta: b) 40 metros.

Exercício resolvido da questão 4 –

Alternativa correta: a) 7.

Exercício resolvido da questão 5 –

Alternativa correta: c) 140 mil km2.

Exercício resolvido da questão 6 –

Alternativa correta: e) 0,30.

Gostou dos nossos Exercícios de Fração? Compartilhe com os seus amigos e comente abaixo sobre algo que você deseja mais explicações.

Nós também queremos te conectar à faculdade! Experimente fazer o Teste vocacional ou procurar uma vaga no seu curso dos sonhos com desconto no Beduka Bolsas. Por lá você pode encontrar o que está procurando e não vai se arrepender de ter se dado uma chance.Boa sorte!