Inequação é uma sentença matemática que é o oposto da equação. Por isso, ela possui uma incógnita e representa uma desigualdade. Por isso, no lugar do “=”, utilizamos os símbolos: >, <, ≥ e ≤. Sua solução é um conjunto numérico que pode ser representado no gráfico, na reta real ou no conjunto solução.
Neste artigo sobre Inequação, você encontrará:
- Como identificar uma inequação?
- Como resolver uma Inequação? Quando se muda o sinal?
- O que é inequação de primeiro e segundo grau?
- Sistema de Inequações
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
Como identificar uma inequação? O que é e exemplos!
A Inequação é o contrário da equação, ou seja, ela é uma sentença matemática que expressa uma desigualdade. Os demais elementos são semelhantes, como a presença de um valor desconhecido (incógnita).
Por esse motivo, no lugar do sinal “=”, usamos os seguintes símbolos na inequação:
- “>” , que lemos como “maior que”
- “<” , que lemos como “menor que”
- “≥” , que lemos como “maior ou igual que”
- “≤” , que lemos como “menor ou igual que”
Exemplos
- 3x – 5 > 62
- 3x – 2 < 34
- 2x + 4 ≥ 2
- 10 + 2x ≤ 20
Como resolver uma Inequação?
O objetivo de resolver uma inequação é descobrir quais os valores para “x” que atendem à condição (menor que, maior que…).
De modo geral, o modo de resolução das inequações é semelhante ao das equações, por seguirem os princípios básicos. Mas ao final ocorrem mudanças e pode haver uma situação em que devemos trocar o sinal para o seu oposto.
Cada tipo de inequação terá seu diferencial, portanto, vamos analisá-las individualmente nos próximos tópicos.
Quando se muda o sinal da inequação?
Numa equação, há momentos em que a incógnita está negativa e precisamos multiplicar toda a sentença por -1. Isso também pode ocorrer em uma inequação, mas nesse caso também precisamos inverter o sinal da desigualdade para o seu oposto!
- Sempre inverteremos o sinal da inequação quando ela for multiplicada ou dividida por um número negativo. Haverá um exemplo no próximo tópico!
O que é inequação de primeiro grau e como resolvê-la?
Uma inequação do 1º grau segue as mesmas condições da equação de primeiro grau, só muda o sinal da igualdade por uma desigualdade.
Sendo a e b números reais e a ≠ 0, além de o maior expoente da incógnita ter de ser 1, temos a forma genérica:
- ax + b >0
- ax + b < 0
- ax + b ≥ 0
- ax + b ≤ 0
Como resolver uma inequação de primeiro grau?
Seguimos aquela lógica básica que foi detalhada no artigo das equações:
1.Eliminar os parênteses (se houver) e fazer as operações prioritárias
2. Efetuar a transposição de termos
3. Reduzir os termos semelhantes
4. Isolar a incógnita
Depois, encontraremos o valor numérico e analisaremos a condição de desigualdade.
Exemplo: resolva a inequação 15 – 7x ≥ 2x – 30
15 – 7x ≥ 2x – 30
– 7x – 2x ≥ – 30 -15
– 9x ≥ – 45
9x ≤ 45 (observe que invertemos o símbolo ≥ para ≤, pois multiplicamos a equação por -1)
x ≤ 45/9
x ≤ 5
Podemos ainda resolver a equação da seguinte forma:
1- Substituir o sinal da desigualdade pelo da igualdade
2 – Passar todos os números para o primeiro membro, zerar o segundo e resolver a equação normalmente
3 – Fazer o estudo do sinal da equação no gráfico, identificando os valores de x que representam o símbolo da inequação.
Como a solução da equação é qualquer número menor ou igual a cinco, trata-se de um conjunto de números, podendo ser representado de três formas: conjunto solução, plano cartesiano ou reta real. Observe:
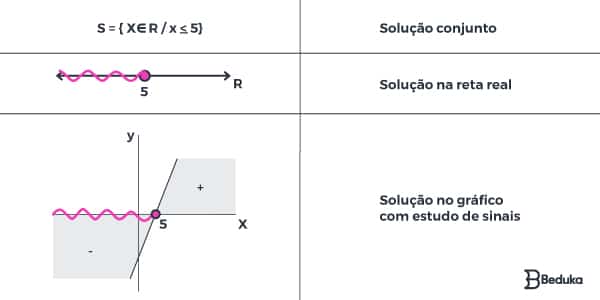
Atenção!
Note que a função pode assumir valor negativo (menor ou igual a zero) com o x tendo valores positivos (1, 2, 3, 4 e 5). Não confunda o sinal da variável e o sinal da função!
Note que a bolinha que contém o 5, na reta real, está colorida / fechada. Isso significa que aquele número pode fazer parte da solução (menor ou igual a 5). A bolinha só estará aberta / incolor se o número não fizer parte da solução (ex: menor que cinco, não inclui o 5).
Sistema de Inequações
Bem como existem os sistemas de equações, também existem os sistemas de inequações!
Nele, precisamos analisar e responder cada inequação separadamente. Depois, comparamos as retas reais de cada uma e encontrar o conjunto solução que satisfaz as duas ao mesmo tempo.
Exemplo:
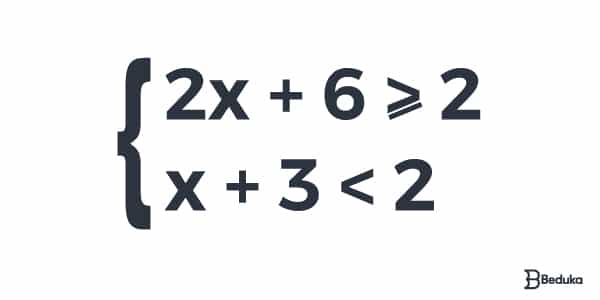
Então, vamos resolver a “inequação I”:
2x + 6 ≥ 2
2x ≥ 2 – 6
2x ≥ -4
x ≥ –4⁄2
x ≥ -2
Portanto, para qualquer valor maior ou igual a -2 satisfaz essa inequação.
Agora vamos resolver a “inequação II”:
x + 3 < 2
x < 2 – 3
x < -1
Portanto, neste problema temos que qualquer valor menor que -1 satisfaz essa inequação.
Então, temos a seguinte solução para o sistema de inequações:
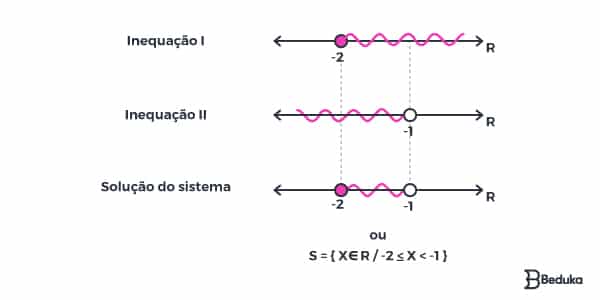
Inequação de segundo grau e como resolvê-la
Uma inequação do 2º grau segue as mesmas condições da equação do segundo grau, só muda o sinal da igualdade por uma desigualdade.
Sendo a, b e c números reais e a ≠ 0, além de ter de haver uma incógnita com expoente 2, temos a forma genérica:
- ax² + bx + c > 0
- ax² + bx + c < 0
- ax² + bx + c ≥ 0
- ax² + bx + c ≤ 0
Como resolver uma inequação de segundo grau?
Neste caso usamos aquela lógica dita acima:
1- Substituir o sinal da desigualdade pelo da igualdade
2 – Resolver a equação normalmente (usando a fórmula de bháskara)
3 – Fazer o estudo do sinal da equação no gráfico, identificando os valores de x que representam o símbolo da inequação.
Exemplo: resolva a inequação x² -x -6 < 0
Note que, pelo sinal da desigualdade, é preciso encontrar valores negativos, cuja expressão do lado esquerdo do sinal < dê uma solução menor do que 0.
Primeiro, identifique os coeficientes:
a = 1 / b = – 1 / c = – 6
Utilize a fórmula de Bhaskara (Δ = b2 – 4ac):
Δ = (- 1)2 – 4 . 1 . (- 6)
Δ = 1 + 24
Δ = 25
Continuando na fórmula de Bhaskara, substituindo o discriminante para encontrar as raízes:
x = (1 ± √25) / 2
x = (1 ± 5) / 2
x’ = (1 + 5)/ 2 e x” = (1 – 5) / 2
x’ = 6 / 2 x” = – 4 / 2
x’ = 3 x” = – 2
Como o coeficiente “a” dessa equação é positivo, seu gráfico terá a concavidade voltada para cima. Traçamos as raízes ( -2 e 3) e observamos a região que condiz com o sinal da inequação: valores negativos da equação.
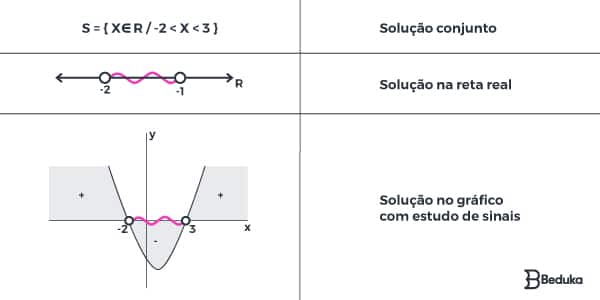
Atenção!
Note que a função pode assumir valor negativo (menor ou igual a zero) com o x tendo valores positivos (1 e 2). Não confunda o sinal da variável e o sinal da função!
Note que as bolinhas que contém o -2 e o 3, na reta real estão incolores / abertas. Isso significa que aquele número não faz parte da solução. A bolinha só estará fechada / colorida se o número poder fazer parte da solução.
Gostou do nosso artigo sobre Inequação? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





