Entenda o que é Permutação, tipos e fórmulas com exemplos!

A Permutação (Pn) é um tipo de agrupamento da análise combinatória em que trocamos a ordem dos elementos de um conjunto. Assim, sabemos quantas são as possibilidades de formar novos agrupamentos com a mesma quantidade de elementos. Há 3 tipos de Combinações que possuem suas próprias fórmulas: simples, com repetição e circular.

Ficou confuso? 

Calma, nós vamos te explicar desde o início!

Neste texto sobre Permutação, você encontrará os tópicos abaixo. Clique em um deles para ir diretamente ao conteúdo:

1. Introdução à Análise Combinatória.
2. O que é Permutação?
3. De onde veio a ideia de Permutação.
4. Símbolo das Permutações.
5. Fórmula das Permutações.
6. Tipos de Permutação e quando usá-las.
7. Permutação Simples + Exemplo de questão resolvida.
8. Permutação com Repetição + Exemplo de questão resolvida.
9. Permutação Circular + Exemplo de questão resolvida.
10. Diferença entre Permutação, Arranjo e Combinação.

• Estudando para as provas? Conheça O melhor Simulado do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!

Introdução à Análise Combinatória

A Análise Combinatória é a área da Matemática que estuda as formas de resolver problemas com contagem de elementos ou possibilidades de algo ocorrer. Ela vai nos dizer quais as técnicas e métodos para cada tipo de situação. 

O Princípio Fundamental da Contagem (PFC) e o Fatorial são contas que aprendemos a fazer desde o Ensino Fundamental, pois eles são a base da análise combinatória e seu raciocínio. Não deixe de ler antes de continuar!

Em outras situações, os cálculos tendem a se tornar complexos. Para facilitar o desenvolvimento das ideias, nós dividimos as técnicas de acordo com as situações. Elas podem ser um caso de Permutação, Arranjo ou Combinação.

O que é Permutação?

Permutação é a quantidade de formas que podemos trocar os elementos de um conjunto “n”. Nessa contagem, buscamos identificar quais são as formas de reorganizar um mesmo conjunto inicial, trocando seus elementos de lugar/ordem.

Quando observamos um conjunto, podemos pegar seus componentes e trocá-los de posição, sem acrescentar ou tirar partes. Assim, o número de elementos do grupo se mantém, mas a ordem desses elementos interfere e nos dá novos resultados.

Exemplo:

Vamos tomar como base um conjunto “n”, que será uma palavra de 3 letras: “SOL”. Se nós queremos ver quais são as possibilidades totais de organizar uma palavra com essas letras, teremos 6 resultados de permutações ao trocá-las de lugar: 

SOL / SLO / LOS / LSO / OSL / OLS  

Cada uma dessas palavras, existentes ou não, é uma permutação de 4 elementos (letras) do conjunto “n” (palavra). 

Por isso, dizemos que se x é uma permutação de n, então x e n são constituídos pelos mesmos elementos, ordenados de formas diferentes.

• Podemos fazer permutação com vários temas diferentes, como números e pessoas. No caso da permutação de letras, chamamos de Anagrama.

De onde vêm as Permutações?

As permutações são casos específicos dos Arranjos Simples. Você pode ler o artigo com a explicação completa, mas vamos resumir aqui para contextualizar:

Arranjos são agrupamentos em que a ordem importa e podemos mudar a quantidade de elementos. É como se pegássemos a palavra “SOL” e contássemos as possibilidades de agrupar suas 3 letras em conjuntos de 2 elementos (SO, OS, LS…). 

Por isso, o Arranjo Simples precisa que o número de componentes do agrupamento seja menor ou igual ao número de elementos do conjunto inicial. Note que esse exemplo não se trata de um anagrama, pois é um arranjo de letras 3 letras 2 a 2, não sua permutação.

Quando o número de elementos do agrupamento é igual ao número de elementos do conjunto inicial, apenas iremos trocar a ordem dos componentes. Aí sim é que chamamos de Permutação.

• São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!

Qual o símbolo das Permutações?

O símbolo que representa a definição de Permutação é:

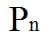
Lemos assim: “permutação de n elementos”

Em que:

• n = número de elementos do conjunto inicial.
• P = quantidade de permutações possíveis.

Dessa forma, representamos o exemplo do primeiro tópico como P3 = 6 (3 letras organizadas em ordens diferentes resultam em 6 possibilidades).

Curiosidade: Você sabia que o nome Iracema, personagem de um dos romances mais famosos de José de Alencar, é um anagrama da palavra América? Teste para conferir!

Quais as fórmulas de Permutação Simples, com Repetição e Circular?

Você viu no tópico anterior que tivemos que montar as permutações manualmente, escrevendo uma por uma. Imagine se a questão pedisse uma P 40… Além de dar trabalho e podermos fazer confusão, o tempo gasto seria enorme.

Pensando justamente nas questões de vestibulares, em que precisamos de agilidade, há fórmulas que nos poupam tempo! Basta substituir cada elemento na posição correta e resolver como uma equação normal. 

Não é necessário gastar tempo montando todas as permutações possíveis, basta aplicar a fórmula de Permutação Simples: P n = n!. Use-a nas situações em que a ordem importa e que apenas iremos trocar a posição de elementos, mantendo sua quantidade.

• Lembre-se: A exclamação (!) na frente do número/letra indica a operação de Fatorial. Por lógica, podemos entender o porquê disso:

Tomando novamente o exemplo dos anagramas da palavra SOL, podemos estabelecer o seguinte raciocínio: 

Há 3 letras para preencher 3 espaços. Não importa qual letra eu pegue primeiro, sempre haverá 3 opções para a primeira “casa”. Depois, haverá duas opções para a do meio e só restará uma para a última casa. 

Seguindo o PFC, sabemos que o esquema será “3.2.1”, o mesmo resultado de 3!

Note que a fórmula da permutação simples também é derivada do arranjo simples. O arranjo é dado por n! / (p-n)!. Porém, quando n=p temos: n!

• Existem ainda outros 2 casos especiais de Permutações: com Repetição e Circular. Falaremos sobre suas diferenças e exemplos no próximo tópico! Já deixamos a fórmula aqui para você ir se familiarizando…

Quais os tipos de Permutação e quando usá-los?

Nós sempre usaremos a Permutação quando a questão der importância à ordem e mantiver o números de elementos nos conjuntos. Ainda assim, existem várias situações diferentes que esses 2 fatores aparecem. 

É daí que surgem os 3 tipos de Permutações: Simples, com Repetição e Circular.

Vamos conhecê-los!

O que é uma Permutação Simples? [Exemplo]

A permutação Simples é aquela em que precisamos fazer as trocas dos elementos de um conjunto, sendo que não há nenhum elemento repetido.

Exemplo

1) A senha de chamada de um escritório possui 4 algarismos. Além disso, ela é sempre formada pelos números do conjunto {2,5,6,8}. Quantas são as senhas disponíveis?

Solução

O primeiro passo é notar que estamos falando de uma permutação, pois a senha tem que ter 4 dígitos e há 4 algarismos diferentes para preenchê-la.

Agora, basta aplicar na fórmula:

P4 = 4!

P4 = 4.3.2.1

P4 = 24 senhas

Permutação com Repetição [Exemplo]

A permutação com Repetição é aquela em que precisamos fazer as trocas dos elementos de um conjunto, mas há elementos repetidos nele. Por causa disso, o raciocínio muda um pouco:

Se um conjunto tiver um determinado elemento repetido, como duas letras“A”, a troca entre esses dois elementos iguais não gera um grupo novo. Por isso, essa repetição deve ser retirada da fórmula de permutações.

Para subtrair as repetições, devemos dividir o número normal de permutações (n!) pela quantidade de repetições do elemento repetido (k!).

Se houver dois elementos repetidos, devemos acrescentar ao denominador a quantidade de vezes que este outro elemento se repete (j!), e assim por diante.

Exemplo

1) Qual é a diferença entre o número de anagramas da palavra ANAGRAMA e ARARA?

Solução

O primeiro passo é sabermos que todos os anagramas são calculados por meio de permutações. Além disso, devemos ficar atentos e observar que cada uma dessas palavras têm um determinado número de elementos que se repetem tantas vezes.

Por isso, vamos usar a fórmula de permutação com repetição e calcular o número de anagramas de cada uma delas, separadamente.

• Palavra ANAGRAMA: Possui 8 letras mas apenas 5 são diferentes (A,N,G,R,M). Observamos então que a letra A aparece 4 vezes. Então:

P₈⁽⁴⁾ = 8! / 4!

P₈⁽⁴⁾ = 8.7.6.5.4! / 4!

P₈⁽⁴⁾ = 8.7.6.5

P₈⁽⁴⁾ = 1 680 anagramas possíveis

• Palavra ARARA: Possui 5 letras mas apenas 2 são diferentes (A,R). Observamos então que a letra A aparece 3 vezes e a letra R aparece 2 vezes. Então:

P5 ^(3,2) = 5! / 3! . 2!

P5 ^(3,2) = 5.4.3! / 3! . 2!

P5 ^(3,2) = 5.4 / 2.1

P5 ^(3,2) = 20 / 2

P5 ^(3,2) = 10 anagramas possíveis

Portanto, a diferença entre o número de anagramas da palavra ANAGRAMA e ARARA é: 1680 – 10 = 1670.

Permutação Circular [Exemplo]

A permutação circular é uma permutação com as mesmas bases das outras, a diferença é que ao invés de os elementos estarem posicionados em uma fila, eles estão em círculo. 

Isso muda tudo, pois um círculo não tem início nem fim. Por isso, dependendo de onde começamos a contar, pode ser que vejamos agrupamentos iguais. Então precisamos retirá-los do número total de permutações.

Para entender melhor, vamos resolver um exemplo:

Exemplo

1) De quantas maneiras uma professora pode organizar 4 criancinhas em uma roda de ciranda?

Solução

Vamos supor que as crianças são Miguel, Carla, Fábio e Alice. A professora colocou-os exatamente nessa ordem, depois, pediu que Miguel e Alice dessem as mãos, formando uma roda.

Se tomarmos como primeira referência o Miguel, teríamos uma possibilidade de roda que começa nele e termina em Alice. Se tomarmos como referência Carla (é uma roda, não tem início nem fim), o último a contar seria Miguel. E assim por diante.

Porém, ainda que tomemos referenciais diferentes para começar a contar, eles não são absolutos já que não se trata de uma fila, mas de uma roda. Por isso, independente de onde começamos a contar, a ordem entre as crianças permanece a mesma.

Note que, nesta disposição e independente de onde contamos, Carla sempre estará entre Miguel e Fábio. Assim como Fábio sempre estará entre Carla e Alice e assim por diante.

Por isso, nesta disposição, há 4 referenciais que nos dão uma mesma ordem. Logo, teremos que retirar 3 casos para não repetir a ordem.

A partir daí surge a fórmula de permutação circular PC n = (n-1)!

Então, o número de permutações circulares diferentes entre 4 crianças será:

PC 4 = (4-1)!

PC 4 = 3!

PC 4 = 3.2.1

PC 4 = 6 possibilidades

Qual a diferença entre Permutação, Arranjo e Combinação?

Nós te dissemos que a análise combinatória é a área que estuda diferentes métodos para diferentes casos, sendo eles: Arranjo, Permutação e Combinação.

A essa altura, você já entendeu o que é Permutação: troca dos elementos de um conjunto, com a ordem sendo importante e sem modificar o números de elementos do grupo. Mas os outros dois são diferentes:

Resumidamente, os Arranjos são agrupamentos em que a ordem também importa, mas mudamos o número do agrupamento. Imagine as senhas de 2 dígitos que podemos fazer com 3 algarismos. 

Já a Combinação é um caso em que a ordem não importa. Imagine a possibilidade de duplas entre 4 crianças. Uma dupla com João e Maria é a mesma que Maria e João, então a ordem não nos dá diferentes resultados.

Gostou do nosso artigo sobre Permutação? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.

Experimente agora!