Os Pontos na matemática e suas funções: saiba o que eles são e como usá-los!

Você já pensou em algo que não pode ser definido, não tem partes ou forma e é adimensional (0 dimensões)? Este é o ponto: o elemento mais básico que forma toda a Geometria. Neste resumo sobre os pontos na matemática, você aprenderá as características e as diferentes formas com que eles são usados!

Neste resumo sobre os pontos na matemática, você encontrará os tópicos abaixo. Se quiser, clique em um deles para ir diretamente ao conteúdo:

1. Introdução: o que é a Geometria?
2. O que é o ponto na matemática?
3. Quais são as funções e propriedades do ponto?
4. Cuidado: diferencie os tipos de pontos!
5. As 3 fórmulas com pontos na Geometria Analítica.

Depois você pode testar o que aprendeu. É só fazer o nosso Simulado ENEM gratuito! Ele pode ser personalizado com as matérias que você quiser.

Introdução: o que é a Geometria?

Antes de tudo, é preciso saber que o ponto é um elemento da Geometria. Isso significa que estamos lidando com uma parte da matemática que se baseia nas representações gráficas (desenhos).

O conceito de ponto surge na Geometria Plana de forma bem básica. Depois, eles são estudados com outra visão na Geometria Espacial. Por fim, são muito usados na Geometria Analítica, uma área que relaciona os desenhos com álgebra.

Nós só estamos querendo te mostrar que esse é um elemento muito básico e importante de ser compreendido. Mas fique tranquilo, nos próximos tópicos explicaremos os conceitos em cada área e daremos exemplos!

O que é o ponto na matemática?

O ponto é um dos entes primitivos da matemática. É a base para construir os outros conceitos dessa área. Ele é o primeiro de todos, então é extremamente simples.

Inclusive, os pontos não possuem uma definição. Então, nós só podemos falar sobre suas características, propriedades e utilidades!

Isso acontece porque eles são adimensionais, ou seja, não possuem dimensão. Assim, não podemos medir sua altura, comprimento ou largura. Sequer podemos definir seu formato.

Como consequência disso, a nossa maneira de representá-lo visualmente, é fazer, literalmente, um pontinho no papel. O “nome” de cada ponto, que vai diferenciar um do outro, é dado por uma letra maiúscula qualquer.

Para finalizar essa ideia, podemos dizer que os pontos são “aquilo que não tem partes”. Nós não podemos dividi-lo, ele é inteiro.

• São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!

Quais são as funções e propriedades do ponto?

Agora que você já entendeu que ele é a base de tudo, nós podemos dizer que só existe geometria porque existe o ponto! Veja só:

A realidade é que o conjunto de pontos alinhados formam uma reta. Já o conjunto de retas formam as figuras planas e espaciais, que são o foco da geometria. Portanto, o ponto constitui a geometria assim como os átomos formam o universo!

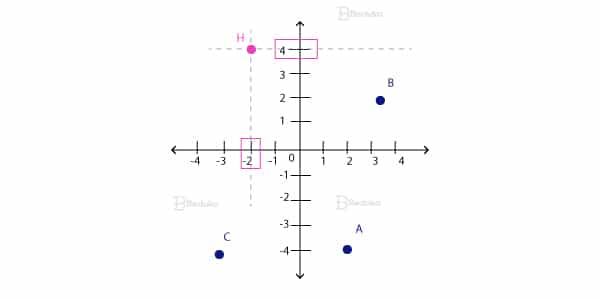
Além disso, a função prática dos pontos é servir como um localizador ou uma referência geográfica.

Pense só: você está olhando um mapa e acha o lugar que queria. Quando for marcar esse lugar, pode até usar o símbolo de um quadrado, estrela ou xis. Mas em qual parte dessas figuras está, exatamente, o lugar que você quer?…

O melhor mesmo é marcar com um ponto. Já que ele não tem partes, ele nos indica a posição com mais precisão, é literalmente alí!

Você já brincou de batalha naval? Se sim, fica mais fácil entender isso. Se não, saiba que eles são ótimo localizadores porque podem ser facilmente identificados pelo sistema de coordenadas no plano cartesiano.

Cuidado: não confunda os pontos!

Já que os pontos são simples, básicos e úteis, é comum que sejam usados em outros contextos. Mas é importante que você saiba diferenciar cada um deles.

O ponto que estamos falando neste artigo pertence à geometria matemática. 

Porém, na lógica matemática, existe um sinal formado por três pontos triangulares. Este sinal (∴) é um símbolo que indica uma conclusão lógica, então costuma ser lido em voz alta como “portanto” ou “então”.

Além disso, você já deve ter visto os sinais de pontuação no Português, que também inclui um ponto. Mas aí até a área é diferente, então você já sabe que se trata de outro assunto!

Agora, vamos voltar para o ponto da vez e finalizar o entendimento sobre ele:

As 3 Fórmulas com pontos na Geometria Analítica

Os vértices das figuras espaciais e planas podem ser identificados por pontos, já que estão justamente na quina. Então, quando vamos estudar as medidas dessas figuras, é uma ótima ideia colocá-las no plano e usar as coordenadas.

Diante disso, podemos saber qual a distância entre dois pontos para achar o lado de uma figura, por exemplo. Também podemos usar os pontos de uma reta para achar a equação que a descreve.

Viu como tudo está relacionado? Esse assunto é tratado na Geometria Analítica e é bem extenso. Por isso, só vamos colocar as 3 fórmulas básicas que focam nos pontos.

• Se você quiser se aprofundar e saber qual a relação do ponto com a reta, com a circunferência e tudo o mais, confira o nosso artigo completo!

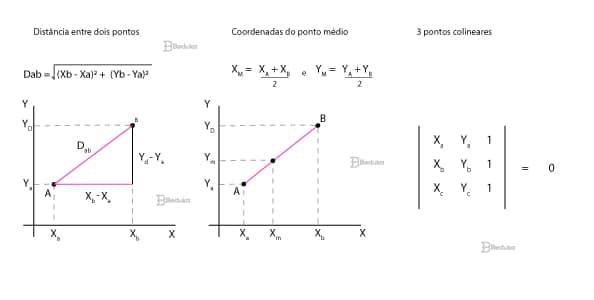
Como calcular a distância entre dois pontos?

Se estivermos querendo saber a distância entre dois pontos quaisquer, como A e B, precisamos anotar as suas coordenadas. Fica assim: A (x_a, y_a) e B (x_b, y_b).

Então, traçamos a distância entre eles e veremos que se forma um segmento de reta. Vamos chamá-lo de d_AB. 

Note que d_AB funciona como a hipotenusa de um triângulo que conseguimos descobrir os outros lados. Isso está representado na imagem do tópico anterior!

Fazemos “x_b – x_a” para achar a medida do cateto (lado) do triângulo que é paralelo ao eixo x. O mesmo foi feito com a operação “y_b – y_a” para achar a medida do cateto paralelo ao eixo y. 

Portanto, basta aplicar o teorema de Pitágoras e substituir essas informações Assim, conseguimos definir uma fórmula genérica para achar a distância entre quaisquer pontos.

d_AB = √ [(x_b – x_a) + (y_b – y_a)]

Exemplo

1) O lado DE de um pentágono é limitado pelos vértices de coordenadas D(5,4) e E(8,5). Determine qual é a medida desse lado.

Solução:

d_DE = √ [(x_e – x_d) + (y_e – y_d)]

d_DE = √ [(8 – 5) + (5 – 4)]

d_DE = √ [(3) + (1)]

d_DE = √[4]

d_DE = 2

Como calcular o ponto médio entre dois pontos?

Na geometria plana, o conceito de ponto médio (M) é aquele que divide um segmento ao meio. 

Na geometria analítica, o raciocínio é semelhante. Se um segmento tem dois pontos (A e B) nas suas extremidades, então o ponto médio M (x_m, y_m) será a média das coordenadas desses pontos!

Sendo assim, basta aplicar as coordenadas dos pontos na fórmula da média:

x_m = (x_a+x_b) / 2 

e

y_m = (y_a+y_b) / 2

Como saber se três pontos distintos são colineares?

Imagine que uma questão te fale de 3 pontos aleatórios. Depois, te perguntam se eles são parte de uma mesma reta. Acontece que não tem nenhum desenho na questão, apenas as coordenadas dos pontos… 

Você saberia resolver? Se não, nós te ajudamos:

Para resolver essa questão, é preciso lembrar que as matrizes são uma forma de organizar informações matemáticas. Além disso, nós podemos fazer uma operação chamada determinante, que resume a matriz em um número só.

Assim, para saber se os três pontos pertencem a uma mesma reta, nós só precisamos de:

• 1° Passo: Criar uma matriz com as coordenadas dos três pontos;
• 2° Passo: Calcular o seu determinante;
• 3° Passo: Se o resultado for 0, então eles fazem parte da mesma reta!

Gostou do nosso resumo sobre os pontos na matemática? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.

Experimente agora!