O plano cartesiano é estruturado por duas retas perpendiculares, ou seja, elas possuem apenas um ponto de interseção formando 90 graus. O formato é como o de uma cruz, ou como o sinal da soma (+). E é todo dividido por valores numéricos. O plano é utilizado para a localização de pontos do sistema de coordenadas, importante para geometria, geografia e outras áreas. Leia nosso resumo e faça os 4 Melhores Exercícios sobre Plano Cartesiano.
Quando você terminar os Exercícios de Plano Cartesiano, coloque em prática todo seu conhecimento com O Melhor Simulado Enem do Brasil.
O Plano Cartesiano foi desenvolvido pelo filósofo René Descartes com o objetivo de localizar pontos em um determinado espaço.
Desde então, ele vem sendo muito utilizado nas mais diversas áreas da Matemática, o que aumenta, e muito, a suas chances de cair no ENEM.
Algumas das áreas que podem utilizar esse recurso são:
- Geometria (plana, espacial e analítica)
- Trigonometria
- Astronomia
- Cartografia
- Física vetorial
- Arqueologia
- Engenharia
- Design
- Forças táticas e militares
- GPS e Navegação (aérea, terrestre e marítima)
Aplique seu conhecimento em Plano Cartesiano resolvendo Exercícios de Equação do 1° Grau.
O que é o Plano Cartesiano?
O Plano Cartesiano é um objeto matemático plano estruturado por duas retas perpendiculares, ou seja, elas possuem apenas um ponto de interseção com um formato parecido com o sinal de adição (+) e todo dividido por valores numéricos. Observe:
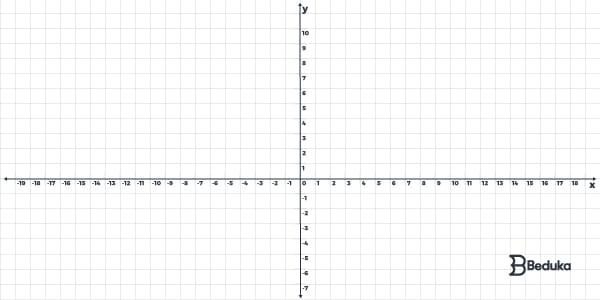
O Plano Cartesiano é aplicado principalmente com o objetivo de localizar elementos em um determinado espaço.
Como é formado o Plano Cartesiano?
O plano cartesiano é formado por duas retas perpendiculares entre si, ou seja, formam um ângulo de 90° (reto).
Elas precisam ser retas numéricas, cheias de números reais equidistantes (mesmo espaçamento entre si), como uma régua.
- Uma das retas está no sentido vertical, esse eixo é chamado de ordenadas e costuma ser representado pela letra “Y”.
- A outra reta está no sentido horizontal, esse eixo é chamado de abscissas e costuma ser representado pela letra “X”.
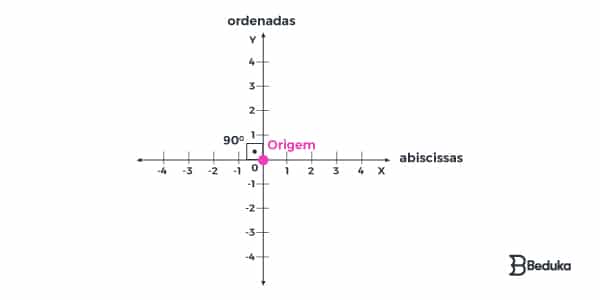
Essas retas só se encontram em um único ponto, chamado de Origem. Ele é o “marco 0” de ambas as retas. Também é o ponto central pois consideramos os valores negativos (à esquerda ou abaixo) e os positivos (à direita ou acima).
Cada ponto na reta está ligado a somente um número real. Como os números são infinitos, as retas também são. Porém, só representamos aqueles que dizem respeito ao contexto da situação que estamos.
Só assim teremos a garantia de que é possível medir, posicionar e localizar as coisas de forma correta.
- Quer conhecer ainda mais? Leia nosso Resumo Completo sobre Plano Cartesiano.
Como calcular as coordenadas de um plano?
Podemos localizar um ponto de maneira muito simples:
- Primeiro: devemos achar o número do par ordenado no eixo das abscissas (Eixo X);
- Segundo: devemos achar o número do par ordenado no eixo das ordenadas (Eixo Y);
- Terceiro: determinar o ponto encontrado representando-o da seguinte forma: (X, Y).
Observe este exemplo:
- Localize o ponto (3, 1).
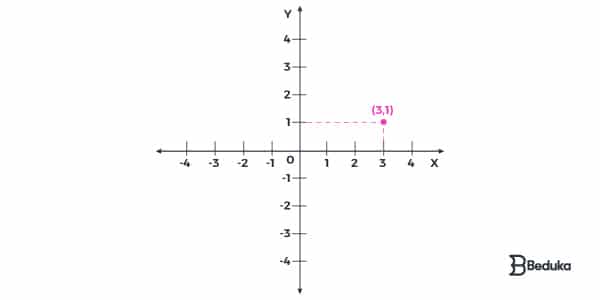
Qual é a estrutura de um Plano Cartesiano? (QUADRANTES)
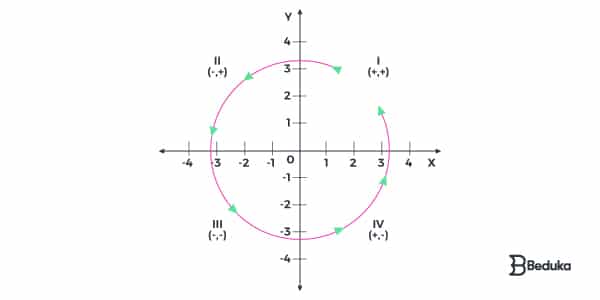
O Plano Cartesiano é dividido em quatro quadrantes:
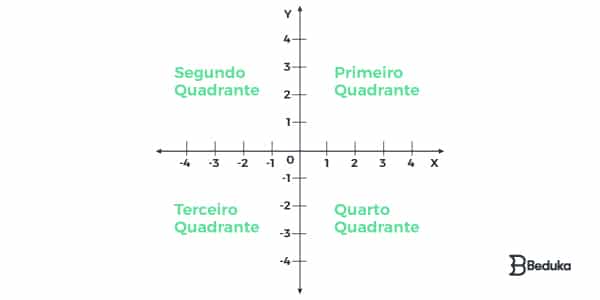
Podemos identificar nesses quadrantes padrões de sinais (negativo ou positivo). Observe como o sinal de X ou Y varia por quadrante:
Quer aumentar ainda mais suas chances de mandar bem no ENEM? Então conheça o Instagram do Beduka, lá postamos diariamente resumos perfeitos para você!
Exercícios de Plano Cartesiano com Gabarito
Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.
Parabéns por ter lido até aqui!
Baixe gratuitamente o Plano de Estudos do Beduka e tenha uma preparação perfeita para o ENEM
Questão 1 – (MACKENZIE) A representação gráfica do conjunto de pontos
(x,y) tais que x−2 − √4 −y2⩾0 é:
a)
b)
c)
d)
e)
Questão 2 – (EPUSP) O ponto P (3, m) é interno a um dos lados do triângulo A (1,2), B (3,1) e C (5,-4). Então:
a) m = -1
b) m = 0
c) m = ½
d) m = 1
e) nenhuma das respostas anteriores
- Ufa, estamos quase no fim! Faça os 2 últimos Exercícios de Plano Cartesiano
Questão 3 – (USP) Uma das diagonais de um quadrado tem extremidades A (1;1) e C (3;3) . As coordenadas dos outros dois vértices são:
a) (2 ; 3) e (3 ; 2)
b) (3 ; 1) e (1 ; 3)
c) (3 ; 0) e (1 ; 4)
d) (5 ; 2) e (4 ; 1)
e) nenhuma das anteriores
Questão 4 – (FUVEST) A equação x² + 2x + y² + my = n, em que m e n são constantes, representa uma circunferência no plano cartesiano. Sabe-se que a reta y = -x + 1 contém o centro da circunferência e a intersecta no ponto (-3, 4). Os valores de m e n são, respectivamente:
a) -4 e 3
b) 4 e 5
c) -4 e 2
d) -2 e 4
e) 2 e 3
- Parabéns, você chegou ao fim dos Exercícios de Plano Cartesiano. Confira agora o Gabarito:
Gabarito dos Exercícios de Plano Cartesiano
Exercício resolvido da questão 1 –
Alternativa correta: b)
Exercício resolvido da questão 2 –
Alternativa correta: a) m = -1
Exercício resolvido da questão 3 –
Alternativa correta: b) (3 ; 1) e (1 ; 3)
Exercício resolvido da questão 4 –
Alternativa correta: a) -4 e 3
Estude para o Enem com o Simulado Beduka. É gratuito!
Gostou dos nossos Exercícios de plano cartesiano? Compartilhe com os seus amigos e comente abaixo sobre as áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.





