A cinemática vetorial é a parte da cinemática que estuda os movimentos que já estão acontecendo, mas sua diferença é observar também os módulos, direções e sentidos dos vetores que representam velocidade, deslocamento e aceleração. Há as fórmulas específicas para cada caso, que confere neste resumo sobre a cinemática vetorial!
Neste texto com o resumo sobre a cinemática vetorial, você encontrará os tópicos abaixo. Se quiser, clique em um deles para ir diretamente ao conteúdo:
- O que é cinemática?
- O que são grandezas escalares e vetoriais?
- Resumo sobre o que é a cinemática vetorial
- Deslocamento vetorial.
- Velocidade vetorial (média, instantânea + fórmula).
- Aceleração vetorial (tangencial, centrípeta, média e resultante + fórmulas).
- Composição de movimentos + exemplo.
- Depois você pode testar o que aprendeu, é só fazer o nosso Simulado ENEM gratuito! Ele pode ser personalizado com as matérias que você quiser.
O que é cinemática?
A cinemática é uma das áreas da Física, sendo aquela que descreve o movimento que já está acontecendo. Ela determina sua posição, a velocidade do corpo e sua aceleração a cada instante.
Isso quer dizer que estuda-se os corpos em movimento, não preocupando-se com a causa desse movimento. A nossa única preocupação aqui é tentar entender o movimento que se faz e as suas características.
De um modo geral, nós falamos mais da cinemática escalar, aquela que estuda:
- Movimento uniforme (MU);
- Movimento circular uniforme (MCU);
- Movimento Retilíneo Uniforme (MRU);
- Movimento Retilíneo Uniformemente Variado (MRUV).
Ah! Você não sabe o que significa “escalar”? Vamos te explicar:
O que são grandezas escalares e vetoriais?
Na física, dizemos que existem 2 tipos de grandezas (coisas a serem medidas). São elas:
- Grandezas escalares: basta um número e sua unidade de medida para entendermos o que é medido. A massa (50 kg) ou a distância (50 m) são exemplos disso.
- Grandezas vetoriais: além do valor e unidade, precisamos também da direção e do sentido para entender a informação completa do que se mede. As forças físicas são exemplos disso.
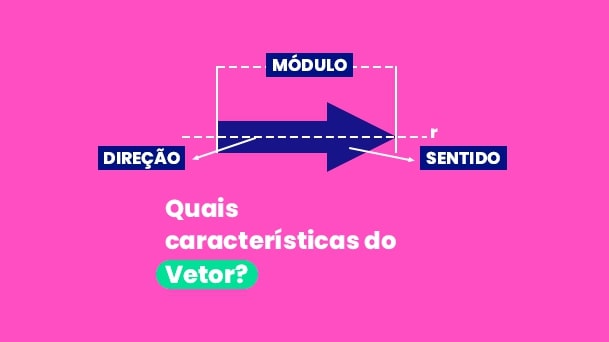
Para representar as informações completas das grandezas vetoriais criaram os vetores. Os vetores são segmentos de reta orientados por estas 3 características:
- Módulo: corresponde à intensidade da força, ou seja, o seu valor numérico.
- Direção: é a própria direção em que o corpo se move ou que a força atua. Pode ser na horizontal ou vertical.
- Sentido: equivale ao lado onde a força é aplicada. Cada direção possui dois sentidos: esquerda e direita quando falamos em horizontal, positivo e negativo quando falamos em vertical.
Todos os vetores são definidos com essas três características ao mesmo tempo. É como um “nome completo”, permitindo sua identificação e diferenciação dos outros.
- É necessário saber também como realizar as operações com vetores e a decomposição vetorial!
Resumo sobre o que é a cinemática vetorial
A cinemática vetorial é a parte da cinemática que estuda os movimentos quando ele está relacionado às grandezas vetoriais. Isso significa que vamos lidar com elementos que são representados por vetores, levando em conta mais de uma dimensão.
Nós vamos continuar analisando deslocamento, posição, distância, aceleração e velocidade. Porém, vamos precisar ainda de uma análise de módulo (ou intensidade), direção e sentido sobre cada elemento que for uma grandeza vetorial.
Agora, vamos analisar cada um deles e, depois, você poderá fazer os exercícios de cinemática vetorial para testar o conhecimento.
O que é deslocamento vetorial?
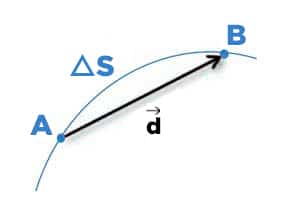
O deslocamento é tido como a diferença entre a posição final e a inicial. Portanto, se uma pessoa começa a andar de um determinado ponto e volta para ele, dizemos que o deslocamento foi nulo embora a distância não seja.
Dando continuidade a essa ideia, o deslocamento vetorial mostra a mudança de posição de um corpo, só que considerando o vetor que tem origem na posição inicial e termina na posição final. Isso independe da trajetória do objeto (se fez curva ou não).
O deslocamento é representado pela letra (d) com uma setinha em cima e é medido em metros (m) de acordo com o Sistema Internacional de Unidades (SI).
- Está gostando do nosso resumo sobre a cinemática vetorial? São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!
O que é velocidade vetorial média?
A velocidade é estudada como a variação da distância em um determinado tempo. Velocidade média é, como diz o nome, a média que se manteve em todo o trajeto.
Quando falamos em velocidade vetorial ela sempre será média, já que estamos analisando todo o caminho percorrido pelo vetor, que já sintetiza as informações.
A velocidade vetorial é o vetor velocidade, indicado pelo (v) com a setinha em cima. Nesse caso, a velocidade possuirá as seguintes características:
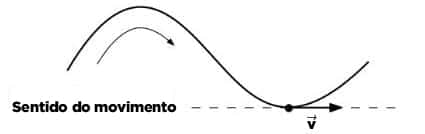
- O sentido será igual ao da trajetória do corpo em velocidade.
- A direção será a mesma da reta tangente à trajetória, no ponto que indica a posição do objeto.
- O módulo será igual ao da velocidade escalar, ou seja, será o módulo do vetor: |v|
Para esse cálculo, é utilizado o deslocamento total (Δd) do objeto e o período de tempo (Δt) para completar todo o caminho. É daí que surge a fórmula:
Vm = Δd/Δt
Em que:
- Vm = velocidade média em metros por segundo (m/s).
- Δd = deslocamento em metros (m).
- Δt = período de tempo em segundos (s).
Lembre-se que cada elemento vetorial (v e d) sempre terá uma setinha em cima dele!
Velocidade vetorial instantânea
A única vez em que não trataremos a velocidade vetorial como média é quando estamos querendo medir a instantânea. Isso é como se déssemos “pause” no movimento e medíssemos a velocidade exatamente alí, naquele segundo.
Como exemplo, temos o movimento circular. Nesse movimento, o vetor velocidade vetorial muda em cada ponto da trajetória, pois, a direção e sentido do vetor muda, mesmo que o módulo permaneça o mesmo.
Sendo assim, o módulo da velocidade vetorial instantânea é igual ao módulo da velocidade escalar naquele instante.
O que é aceleração vetorial?
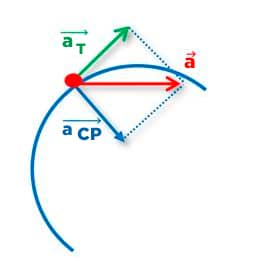
Se a velocidade é dada como um vetor, a aceleração também será. Isso porque a aceleração é definida como a variação da velocidade em um determinado período de tempo.
Mas, neste contexto, ela será dada pela composição de dois vetores:
Aceleração tangencial (at)
É aquela que altera o módulo da velocidade vetorial, indicando se está acelerando ou freando. Suas características são:
- Sua intensidade é igual à da aceleração escalar.
- Sua direção é tangente à curva da trajetória.
- Seu sentido será o mesmo da velocidade vetorial se o movimento for acelerado. Se for um movimento retardado, o sentido será oposto.
Por isso ela pode ser calculada por:
at = Δv / Δt
Em que:
- at = aceleração tangencial em metros por segundo ao quadrado (m/s²).
- Δv = variação da velocidade (final menos inicial) em metros por segundo (m/s).
- Δt = variação do tempo em segundos (s).
Lembre-se que cada elemento vetorial (a e v) sempre terá uma setinha em cima dele!
Aceleração centrípeta (ac)
É aquela que altera a direção da velocidade vetorial, já que está ligada à presença de uma trajetória curvilínea. Suas características são:
- A direção é sempre perpendicular à velocidade vetorial.
- Seu sentido está para o centro da curvatura.
- Sua intensidade é dada por uma fórmula que deixaremos abaixo.
Se a trajetória for retilínea, não existe aceleração centrípeta. Sendo assim, ela depende de dois fatores:
- Velocidade: quanto maior a velocidade, maior a aceleração centrípeta necessária para manter o corpo na curva.
- Raio da curva: quanto menor o raio da curva, maior a aceleração centrípeta necessária para manter o corpo na curva.
Por isso ela pode ser calculada por:
ac = v² / r
Em que:
- ac = aceleração centrípeta em metros por segundo ao quadrado (m/s²).
- v = velocidade em metros por segundo (m/s).
- r = raio da circunferência em metros (m).
Lembre-se que cada elemento vetorial (ac) sempre terá uma setinha em cima dele!
Aceleração resultante
Se temos dois vetores compondo uma aceleração, ela inteira será chamada de aceleração resultante. Portanto, a aceleração resultante é a adição vetorial das duas acelerações ac e at.
Por isso:
a² = at² + ac²
Em que:
- a = aceleração vetorial resultante em metros por segundo ao quadrado (m/s²).
- at = aceleração tangencial em metros por segundo ao quadrado (m/s²).
- ac = aceleração centrípeta em metros por segundo ao quadrado (m/s²).
Lembre-se que cada elemento vetorial (a, at e ac) sempre terá uma setinha em cima dele!
Note que esta fórmula é a mesma do Teorema de Pitágoras, já que decompomos o vetor pelo método do paralelogramo!
Aceleração média
Da mesma forma que a velocidade é média, a aceleração também o é. Isso significa que ela até pode variar durante cada momento do percurso, mas ao final, podemos estipular um valor mediano para representar todo o percurso.
Para calculá-la, é preciso utilizar a variação da velocidade vetorial (Δv) e o período de tempo. Assim, temos a seguinte fórmula:
am = Δv/Δt
Em que:
- am = aceleração média em metros por segundo ao quadrado (m/s²).
- Δv = variação da velocidade (final menos inicial) em metros por segundo (m/s).
- Δt = variação do tempo em segundos (s).
Lembre-se que cada elemento vetorial (a e v) sempre terá uma setinha em cima dele!
Composição de movimentos
Há alguns movimentos que acontecem combinados e são percebidos como uma coisa só, embora tenham direções diferentes. Exemplo disso é o carrossel que gira em torno do seu eixo enquanto os cavalos sobem e descem.
A construção dessa imagem é semelhante ao gráfico de uma função Seno.
Outro exemplo, é quando um barco está atravessando um rio de uma margem a outra e a correnteza faz com que realize um movimento diagonal.
Por isso, quando vamos resolver um problema com mais de um vetor atuando, é necessário considerá-los separadamente e depois entender a composição dos movimentos.
Exemplo
- Um barco deseja atravessar o rio em linha reta, margem à margem, com uma velocidade vetorial de 15 m/s. A correnteza desse rio segue na velocidade de 6 m/s. Qual é a velocidade vetorial resultante com que o barco se desloca?
Resolução:
Note que o barco andará em linha reta de um lado do rio para o outro, enquanto a correnteza atravessa esse trajeto. Por isso, essas velocidades são perpendiculares entre si.
Agora é só fazer a soma vetorial, lembrando-se do teorema de Pitágoras!
a² = b² + c²
v² = 15² + 6²
v² = 225 + 36
v² = 261
v = √261
v = 16,1 m/s
- Se ele estivesse realizando um deslocamento a favor da correnteza, era só somar a velocidade vetorial dele com a da corrente. Se estivesse contra, era só subtrair! Aí teríamos:
Barco contra a correnteza: (15 – 6) = 9 m/s.
Barco a favor da correnteza: (15 + 6) = 21 m/s.
Gostou do nosso artigo com o resumo sobre a cinemática vetorial? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!