Uma Função Exponencial é caracterizada pela presença da variável (x) no expoente de uma base numérica. Como toda função, há uma relação de dependência entre o valor de Y e esse expoente. Além disso, para que seja uma função real, é necessário que a base seja diferente de 1 e alguns outros detalhes… Fique conosco para saber tudo sobre Função Exponencial!
Neste artigo, você encontrará:
- O que é Função Exponencial: definição e importância
- Propriedades e condições da Função Exponencial
- Construção do Gráfico da função
- Exemplos
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
O que é Função Exponencial: definição
Podemos escrever uma função exponencial qualquer usando a definição geral:
- f: R→R tal que y = aˣ, sendo que a > 0 e a ≠ 1
Para facilitar, confira exemplos numéricos de funções exponenciais:
- y = 2ˣ + 1
- y = 0,3ˣ
- y = 5ˣ
Como resolvemos essa conta? Calma lá!
Dizemos que uma função é exponencial quando a variável (x) encontra-se no expoente de uma base (a). Essa base deve ser um número real, maior que zero e diferente de um. Essa condição pode não fazer sentido agora, mas explicaremos o porquê no próximo tópico!
Para avançarmos, é preciso que você já tenha alguns conhecimentos sobre: funções (1° grau, 2° grau, constante, afim…), potenciação, raiz quadrada e equações exponenciais!
Não se esqueça destes detalhes:
- Ser uma função significa ter dependência, ou seja, o valor da função (y) se modifica à medida que modificamos o valor de x, pois o resultado depende da conta que é feito com o outro número.
- Como se trata de uma função, um determinado valor de x produzirá um valor de y, logo, devemos resolver as funções pensando nos pares ordenados (x,y) que se adequam àquela regra. Assim, sempre será dado o valor de um deles para que possamos chegar ao outro.
- Quando usamos a expressão “f(x)” estamos nos referindo ao valor final daquela função de acordo com o valor que colocamos em x, ou seja, referimo-nos ao valor de Y. Logo, Y = f(x).
- Como você pode observar, somar um mesmo número repetidas vezes com ele mesmo é fazer a multiplicação: 2 + 2 + 2 = 2 x 3. Assim, multiplicar um número por ele mesmo repetidas vezes é fazer potenciação: 2 x 2 x 2 = 2³.
Se na multiplicação o resultado cresce de forma linear, dizemos que na potenciação o resultado cresce de forma exponencial. Compare as sequências:

Importância e aplicabilidade da função exponencial
Como você observou, as contas exponenciais apresentam resultados muito grandes em menos tempo. Por causa disso, é considerada uma importante ferramenta da Matemática e está presente em situações nos cálculos que levariam muito mais tempo se fossem usadas outras operações.
Na área financeira serve para calcular uma aplicação à taxa de juros compostos, na Química calcula-se o decaimento radioativo, na Biologia calcula-se o crescimento de bactérias em uma colônia, na Geografia mede-se o crescimento populacional…
Propriedades e condições da Função Exponencial
Vejas as propriedades fundamentais e necessárias para fazer os exercícios em geral. São regras que não podem ser quebradas, ou a função deixará de ser exponencial e os resultados e gráficos darão errado.
1° Condição geral: a base não pode ser negativa
Como estamos falando em exponencialidade, necessariamente falamos sobre potenciação. Assim, se pensarmos na fórmula geral: y = aˣ e quisermos colocar um número negativo, veremos que não há resultado possível!
Exemplo: Vamos supor que o -9 esteja elevado a um número fracionado, como quando o X vale ½. Pelas regras da potenciação, elevar um número a ½ é fazer sua raiz quadrada. Contudo, é impossível tirar a raiz de um número negativo. Por este motivo a base não pode ser menor que zero.
2° condição geral: a base deve ser diferente de 1
De acordo com as regras da potenciação, o número 1 elevado a qualquer número resulta sempre em 1. Portanto, não importa qual valor atribuímos ao X, o resultado Y sempre será 1. Dessa forma, teremos o gráfico de uma função constante e não exponencial.
Exemplo:
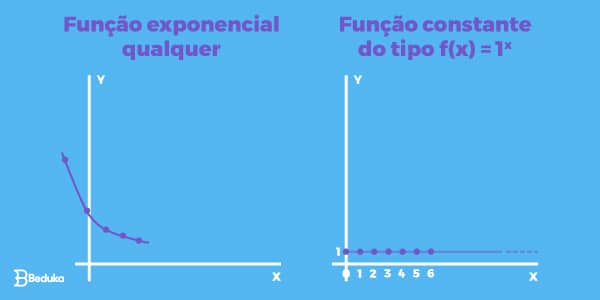
3° condição geral: a base não pode ser igual a 0
Novamente, resgatando os conceitos da potenciação, não existe resultado Real para a operação de elevar 0 a algum expoente. Portanto, a base não pode ser 0.
- 1ª propriedade: se x = 0, então f(x) = 1
As noções de potenciação nos apontam que qualquer número elevado a 0 é sempre igual a 1.
Exemplo: observe as funções f(x) = 3ˣ e f(x) = 2ˣ:
f(x) = 3ˣ → f(0) = 3⁰ → f(0) = 1 → Y = 1
f(x) = 2ˣ → f(0) = 2⁰ → f(0) = 1 → Y = 1
Atenção!
Cuidado para não confundir o fato de o número 0 não poder estar na base mas poder ser a variável (o expoente)!
- 2ª propriedade: se a > 1, a função será crescente
Uma função tem valores crescentes sempre que a > 1, independente do valor de x. O que importa é identificar que aˣ¹ < aˣ².
Exemplo: supondo a função f(x) = 3ˣ, neste caso a = 3 e 3 > 1. Vamos atribuir ainda os valores x₁ = 1 e x₂ = 2 seguindo a ordem numérica x₁ < x₂. Teremos:
f(x₁) = 3ˣ¹ e f(x₂) = 3ˣ²
f(1) = 3¹ e f(2) = 3²
f(1) = 3 < f(2) = 9
Então aˣ¹ < aˣ² porque 3 < 9. Logo, f(x) é uma exponencial crescente!
- 3ª propriedade: se 0 < a < 1, a função será decrescente
Já que a base (a) não pode ser negativa e nem 0 ou 1, o único modo da função ser decrescente é se (a) estiver entre 0 e 1! As condições x₁ < x₂ e 0 < a < 1 também podem ser representadas por uma expressão única: aˣ¹ > aˣ² é típico de uma função decrescente..
Exemplo: Vejamos a função f(x) = 0,5ˣ, em que a = 0,5. Atribuindo os valores x₁ = 1 e x₂ = 2, teremos:
f(x₁) = 0,5ˣ¹ e f(x₂) = 0,5ˣ²
f(1) = 0,5¹ e f(2) = 0,5²
f(1) = 0,5 > f(2) = 0,25
Então aˣ¹ > aˣ² porque 0,50 > 0,25. Logo, f(x) é uma exponencial decrescente!
- 4ª propriedade: sempre que x₁ = x₂, aˣ¹ = aˣ²
Todas as vezes que houver um sinal de igual entre as potências e tivermos a mesma base, as funções devem apresentar o mesmo resultado, ou seja, estão sobre o mesmo expoente.
Exemplo: Suponha que foi dada a função f(x) = 7ˣ. Se o enunciado quiser saber quanto vale x₁ e x₂ e der a informação de que f(x₁) = 49 e f(x₂) = 49, basta organizar e substituir os dados
Teremos que: 49 = 7ˣ¹ e 49 = 7ˣ²
Pela lógica da potenciação, podemos concluir que x₁ = x₂ = 2, pois 7 só será igual a 49 se estiver elevado a 2.
Outras informações importantes
- Juros compostos é função exponencial!
Quando decoramos as fórmulas da matemática financeira pela primeira vez, lá no Fundamental, não nos damos conta de que ela é uma função exponencial que vemos no Ensino Médio!
Já notou que quanto mais tempo(x) passa, maior é o montante (y)? É porque se trata de uma função exponencial, observe a fórmula:
M=C(1+i)t
Viu como é fácil? você já resolvia essas operaçõe sem saber!
- Função exponencial de base “e” (número neperiano)
Assim como sabemos do π (número pi), que possui um valor constante; também há o número “e”, conhecido como constante de Euler ou número neperiano.
Não se assuste! Nós estamos habituados a resolver contas de trigonometria e geometria usando o pi e faremos o mesmo com a constante de Euler. Ou o valor nos é dado e substituímos, ou deixamos na sua forma algébrica e resolvemos a equação normalmente, simplificando os termos quando possível.
Caso você veja algo do tipo f(x)=eˣ, já sabe do que se trata!
Construção do Gráfico da função + exemplo
Como uma função é uma relação de dependência que resolvemos com os valores de pares ordenados; para construir um gráfico é necessário pegar uma função qualquer e estipular valores na variável (X) para encontrar o valor da função Y. Depois, é só colocar no plano cartesiano!
Exemplo: Vamos tomar as funções f(x) = 2ˣ + 2 e f(x) = 0,5ˣ + 3
Como o X é a variável e não há restrições, podemos atribuir qualquer valor a ele. As possibilidades são infinitas, mas procure usar valores pequenos para não complicar sua conta! (Como: -2,-1,0,1,2)
Depois de substituir, é fácil achar o valor de Y em função de x. Resolvemos as contas utilizando as propriedades da potenciação:


Com os pares ordenados em mãos, podemos construir os gráficos:
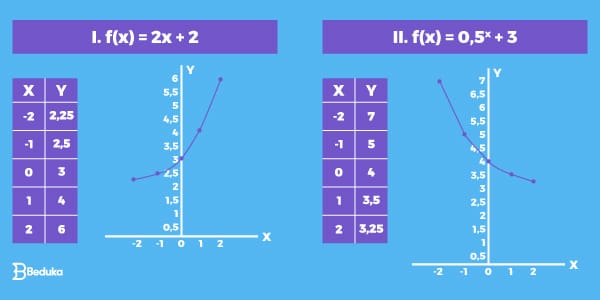
Importante:
- Observe que a primeira função é crescente. Podemos concluir isso tanto pela base ser > 0 quanto pelo desenho que forma no gráfico. Lembre-se que o sentido dessa leitura é sempre da direita para a esquerda.
- Já a segunda função é decrescente. Novamente, podemos concluir por causa da base estar entre 0 e 1 e pelo desenho no gráfico.
- Note ainda que numa função exponencial nunca se chega ao valor Y=0, ou seja, não há nenhum valor da variável que faça a curva tocar o eixo x. Isso acontece porque para a função valer 0 seria preciso que algum número resultasse em 0 após ser elevado. Mas isso não existe!
Gostou do nosso artigo sobre Função Exponencial? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





