O que são funções trigonométricas? Resumo completo!

As funções trigonométricas são aquelas que possuem seno, cosseno ou tangente na sua lei de formação. A característica delas é ser angular e periódica, algo que analisamos ao desenhar o ciclo trigonométrico com um triângulo retângulo. Cada um de seus tipos tem um gráfico e propriedades específicas.

Neste texto sobre o que são funções trigonométricas, você encontrará os tópicos abaixo. Clique em um deles para ir diretamente ao conteúdo:

1. O que é uma função?
2. O que são funções trigonométricas?
3. Conceitos básicos da trigonometria.
4. Como funciona o ciclo trigonométrico?
5. O que são funções periódicas?
6. Qual é a função seno? (características, propriedades e gráfico)
7. Qual é a função cosseno? (características, propriedades e gráfico)
8. Qual é a função tangente? (características, propriedades e gráfico)
9. Como calcular funções trigonométricas? (exercício + solução)

• Estudando para as provas? Conheça O melhor Simulado do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!

O que é uma função?

As funções são expressões numéricas e algébricas (números e letras) que possuem dois lados separados pelo sinal de igual (=). Os valores que desconhecemos são as incógnitas, representadas por letras.

De um lado temos o “f(x)” que representa o valor final da função. Esse valor também pode ser representado por “y”. Do outro lado, temos a regra matemática, ou seja, um conjunto de números que rodeiam o valor “x”. 

Cada tipo de função obedece a uma regra/estrutura básica, chamada lei de formação. Ela define a “cara” de cada função: de qual tipo ela será e como é seu gráfico. 

A expressão “em função de” gera uma ideia de dependência. Então, o valor da função “f(x)” ou “y” se modifica à medida que mudamos o valor de “x”. Assim, resolver uma função é pensar nos pares ordenados (x , y) que se adequam àquela regra.

O que são Funções Trigonométricas?

As Funções Trigonométricas também podem ser chamadas de funções circulares, periódicas ou angulares. Todos esses nomes se devem às suas características principais, que são consequências da sua lei de formação: 

• Angular porque estão relacionadas às voltas e ângulos de um círculo;
• Trigonométrica porque este círculo é o ciclo trigonométrico;
• Periódica porque formam um gráfico com desenhos que se repetem.

Antes de continuarmos, é essencial que você já saiba certos conceitos, porque essa já é uma parte “mais pra frente” da matéria. Nos próximos tópicos, vamos deixar o resumo de alguns conceitos básicos para já ir ativando a sua memória.

Porém, se você não viu essas matérias ou não entende muito bem, é melhor que você estude sobre os outros assuntos antes, os que deixamos explicados nos links acima!

Relembre: o que é trigonometria?

A trigonometria é a parte da matemática que estuda as relações entre os ângulos e os lados dos triângulos retângulos. De modo geral, as relações que nos interessam agora são:

• O Seno de um ângulo é o valor que encontramos ao dividir seu cateto oposto pela hipotenusa.

• O Cosseno de um ângulo é o valor que encontramos ao dividir seu cateto adjacente pela hipotenusa.

• A Tangente de um ângulo é o valor que encontramos ao dividir o cateto oposto pelo cateto adjacente.

Importante: um certo ângulo α tem seno, cosseno e tangente. Os valores dessas relações sempre serão os mesmos, ainda que esse ângulo esteja em outro triângulo com lados diferentes.

São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!

Relembre: como é o ciclo trigonométrico?

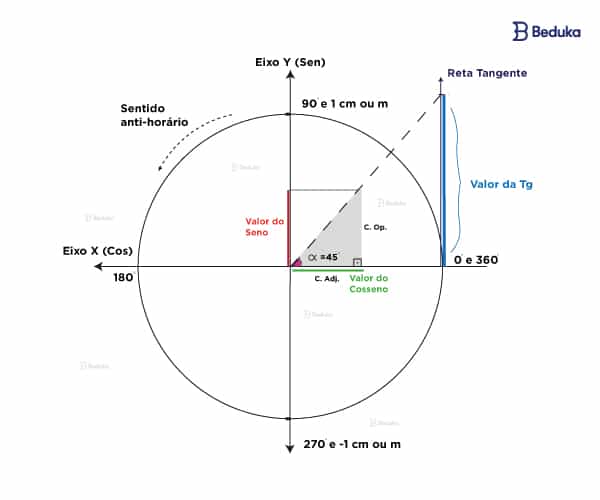
O ciclo trigonométrico é um gráfico em forma de circunferência, desenhado no meio do plano cartesiano. Ele possui características muito importantes:

• O raio da circunferência sempre vale 1;
• Seus ângulos vão de 0° a 360° (volta completa) sendo que o início e o fim estão em um mesmo ponto, o lado “leste” da figura;
• Lemos o ciclo no sentido anti-horário;
• O eixo “y” representa os possíveis valores do seno;
• O eixo “x” se refere aos possíveis valores do cosseno;
• A tangente é uma reta que traçamos ao lado do círculo. Ela só encosta no ponto de origem;
• Podemos dividi-lo em 4 quadrantes e fazer o estudo dos sinais;
• Seus ângulos podem ser medidos em Radiano.

Com base nessas características e nas definições de seno cosseno e tangente, concluímos que:

• Se queremos projetar o valor do seno, deverá ser no eixo y, então o seno sempre varia de 0 a 1. Se o triângulo está dentro do ciclo, a projeção do seno no eixo y é igual ao tamanho do cateto oposto.

• Para projetar o valor do cosseno, deverá ser no eixo x, então o cosseno também varia de 0 a 1. Se o triângulo está dentro do ciclo, a projeção do seno no eixo y é igual ao tamanho do cateto adjacente.

• A projeção da tangente deverá ser feita na reta tangente, então há infinitos valores possíveis. O valor da projeção é igual a altura em que ela bater na reta.

Relembre: o que são funções periódicas?

Ser periódico significa repetir algum comportamento. Portanto, as funções periódicas são aquelas que observamos um mesmo desenho no gráfico se repetir (um mesmo resultado) em certos intervalos de tempo.

• Período: menor intervalo de tempo em que acontece 1 repetição.

Como você deve estar imaginando, as funções trigonométricas são um dos exemplos de funções periódicas. Vamos conhecê-las:

Quais são as funções trigonométricas?

As três principais funções trigonométricas são: 

• Função Seno;
• Função Cosseno;
• Função Tangente.

Lembre-se que, ao falar de funções, estamos considerando os valores pertencentes ao conjunto dos números reais.

Vamos conhecer todas as características de cada uma delas em particular:

Função do seno

A função trigonométrica que chamamos de função seno é aquela que possui o seno na sua lei de formação, assim:

y = sen(x)

Isso significa que:

• Em “x” colocamos o valor do ângulo que queremos;
• O “y” será o valor da projeção desse ângulo.

Quais são as características e propriedades da função seno?

Imagem da função seno

A Imagem da função seno, que são os possíveis valores de y, serão números entre -1 e 1. Isso porque o raio do ciclo trigonométrico é 1 e estamos falando de um universo onde consideramos os números do conjunto dos Reais. 

Assim:

Im = {y ∈ R / -1 ≤ y ≤ 1}

Domínio da função seno

O domínio da função seno, que são os possíveis valores de x, serão infinitas possibilidades de números! Isso porque há infinitos valores de ângulos possíveis, mesmo que o ciclo só vá até 360°.

Isso só é possível porque estamos falando em um círculo, ou seja, uma figura onde não há começo ou fim e tudo são voltas. Portanto, um ângulo de 750° seria o mesmo que:

Comece no 0° e dê a volta completa até chegar em 360°. Continue contando e chegue à segunda volta completa que equivalerá a 720° (360 x 2 = 720). Agora só falta andar os 30° graus restantes para dar 750°. Por isso, no gráfico do ciclo, 750° equivale a 30°.

Assim:

D = {x ∈ R}

Interpretação dos quadrantes da função seno

Se a função y = sen(x) é projetada nos valores do eixo y, então: 

• A função é positiva para os ângulos do 1° e 2° quadrantes(projeções na reta y acima da origem);
• A função é negativa para os ângulos do 3° e 4° quadrantes (projeções na reta y abaixo da origem).

Onde a função seno é crescente e decrescente?

Já te dissemos que no ciclo trigonométrico nós fazemos a leitura no sentido anti-horário. Tendo isso em mente, observe uma coisa interessante:

Se pegarmos dois ângulos em ordem crescente e que pertencem ao primeiro quadrante, os resultados dos senos são crescentes também. Ex: sen 30° = 0,50 e sen 40° = 0,75.

Porém, se pegarmos dois ângulos em ordem crescente e que sejam do segundo quadrante, os resultados dos senos são decrescentes. Ex: sen 150° = 0,50 e sen 160° = 0,34. 

Seguindo essa lógica, dizemos que:

• A função seno é crescente no 1° e 4° quadrantes;
• A função seno é decrescente no 2° e 3° quadrantes. 

Como interpretar o gráfico da função seno?

Se a função não pode assumir valores maiores que 1 ou menores que -1, então já temos uma delimitação no plano. 

Além disso, a montagem de todo gráfico sempre segue as etapas:

• 1°Passo: faça uma tabela com duas colunas x e y;
• 2° Passo: estipule valores para colocar em x e anote na tabela;
• 3° Passo: resolva a função para cada valor de x e anote o resultado do y encontrado na tabela. Sugerimos usar os valores dos principais ângulos do ciclo (0°, 90°, 180°, 270° e 360°) ;
• 4° Passo: agora você já tem pares ordenados para traçar no plano. Marque todos os pontos;
• 5° Passo: ligue os pontos com uma linha e veja a imagem do gráfico se formar! Como estamos falando de ciclo trigonométrico, não ligue com retas, mas com curvas.

Veja:

Valores de x (possíveis ângulos)	Valores de y (resultado do sen)
0° ou 0 rad	0
90° ou π/2 rad	1
180° ou π rad	0
270° ou 3π/2 rad	-1
360° ou 2π rad	0

Curiosamente, os valores do seno ficam variando entre -1, 0 e 1. Além disso, eles se repetem seguindo uma ordem: 0, 1, 0 e -1. 

Depois, continuam: 0, 1, 0 e -1… Ela é mesmo periódica!

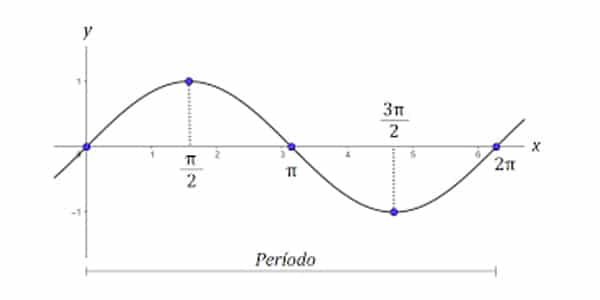
Como está em um formato de onda, dizemos que o período da função seno é 2π porque a ondulação começa no 0 e se repete após o 360°. 

Além disso, você pode ir recheando a lei dessa função com números que multiplicam ou dividem o x, vamos chamá-lo de k. Dessa forma, os possíveis valores da função podem ser expressados por (x + 2πk).

A forma do seu gráfico recebe o nome de senóide.

Função cosseno

A função trigonométrica que chamamos de função cosseno é aquela que possui o cosseno na sua lei de formação, assim:

y = cos(x)

Isso significa que:

• Em “x” colocamos o valor do ângulo que queremos;
• O “y” será o valor da projeção desse ângulo.

Quais são as características e propriedades da função cosseno?

Imagem da função cosseno

A Imagem da função cosseno, que são os possíveis valores de y, serão números entre -1 e 1. Isso porque o raio do ciclo trigonométrico é 1 e estamos falando de um universo onde consideramos os números do conjunto dos Reais. 

Assim:

Im = {y ∈ R / -1 ≤ y ≤ 1}

Domínio da função cosseno

O domínio da função cosseno, que são os possíveis valores de x, serão infinitas possibilidades de números! Isso porque há infinitos valores de ângulos possíveis, como explicamos nos tópicos acima.

Portanto:

D = {x ∈ R}

Interpretação dos quadrantes da função cosseno

Se a função y = cos(x) é projetada nos valores do eixo x, então: 

• A função é positiva para os ângulos do 1° e 4° quadrantes (projeções na reta x afrente da origem);
• A função é negativa para os ângulos do 2° e 3° quadrantes (projeções na reta x atrás da origem).

Onde a função cosseno é crescente e decrescente?

Para saber isso, vamos usar o mesmo raciocínio desenvolvido anteriormente:

Se pegarmos dois ângulos em ordem crescente e que pertencem ao primeiro quadrante, os resultados dos cossenos são decrescentes. Ex: cos 30° = 0,87 e cos 40° = 0,77.

Porém, se pegarmos dois ângulos em ordem crescente e que sejam do terceiro quadrante, os resultados dos cossenos são crescentes. Ex: cos 190° =  – 0,98 e cos 200° = – 0,94. 

Seguindo essa lógica, dizemos que:

• A função cosseno é crescente no 3° e 4° quadrantes;
• A função cosseno é decrescente no 1° e 2° quadrantes. 

Como interpretar o gráfico da função cosseno?

Como já dissemos, a montagem de todo gráfico sempre segue as 5 etapas:

• 1°Passo: faça uma tabela com duas colunas x e y;
• 2° Passo: estipule valores para colocar em x e anote na tabela;
• 3° Passo: resolva a função para cada valor de x e anote o resultado do y encontrado na tabela. Sugerimos usar os valores dos principais ângulos do ciclo (0°, 90°, 180°, 270° e 360°) ;
• 4° Passo: agora você já tem pares ordenados para traçar no plano. Marque todos os pontos;
• 5° Passo: ligue os pontos com uma linha e veja a imagem do gráfico se formar! Como estamos falando de ciclo trigonométrico, não ligue com retas, mas com curvas.

Assim:

Valores de x (possíveis ângulos)	Valores de y (resultado do cos)
0° ou 0 rad	1
90° ou π/2 rad	0
180° ou π rad	-1
270° ou 3π/2 rad	0
360° ou 2π rad	1

Da mesma forma que a função seno, a função cosseno fica variando entre -1, 0 e 1. A diferença é que a função cosseno se repete em uma outra ordem: 1, 0, -1, 0.

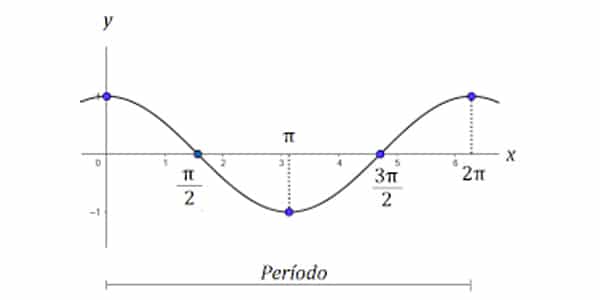
Portanto, dizemos que o período da função cosseno também é 2π. 

Sendo assim, podemos reescrever qualquer valor da função como (x + 2πk). 

Além disso, a forma do seu gráfico recebe o nome de cossenóide.

Função tangente

A função trigonométrica que chamamos de função tangente é aquela que possui a tangente na sua lei de formação, assim:

y = tg(x)

Isso significa que:

• Em “x” colocamos o valor do ângulo que queremos;
• O “y” será o valor da projeção desse ângulo.

Quais são as características e propriedades da função tangente?

Imagem da função tangente

A Imagem da função tangente, que são os possíveis valores de y, serão infinitos números pertencentes aos reais! Isso porque a projeção do valor da tangente se dá na reta, que é infinita.

Assim:

Im = {y ∈ R}

Domínio da função tangente

O domínio da função tangente, que são os possíveis valores de x, poderá ser qualquer valor com duas exceções: se tentarmos projetar a tangente de 90° e 270°, será impossível. Isso porque nos daria uma reta paralela, ou seja, não encontra a tangente e não há como medir.

Portanto:

D = {x ∈ R / x ≠ π / 2 + kπ, k ∈ Z}

Interpretação dos quadrantes da função tangente

Se a função y = tg(x) é projetada nos valores da reta tangente, então: 

• A função é positiva para os ângulos do 1° e 3° quadrantes (projeções na reta tg acima da origem);
• A função é negativa para os ângulos do 2° e 4° quadrantes (projeções na reta tg abaixo da origem).

Onde a função tangente é crescente e decrescente?

Se aplicarmos o mesmo raciocínio que usamos para descobrir o crescimento das funções seno e o cosseno (nos tópicos anteriores), veremos que a função tangente é sempre crescente! 

Como interpretar o gráfico da função tangente?

Como já dissemos, a montagem de todo gráfico sempre segue as 5 etapas que ensinamos nos tópicos acima. Vamos direto para a tabela.

Para obter mais números, pegamos o ângulo notável 45° e seus equivalentes. Agora, temos uma tabela mais completa:

Valores de x (possíveis ângulos)	Valores de y (resultado da tg)
0° ou 0 rad	0
45° ou π/4 rad	1
90° ou π/2 rad	não existe
135° ou 3π/4 rad	-1
180° ou π rad	0
225° ou 5π/4 rad	1
270° ou 3π/2 rad	não existe
315° ou 7π/4 rad	-1
360° ou 2π rad	0

A função tangente se repete em uma outra ordem: 0, 1, (nada) e -1.

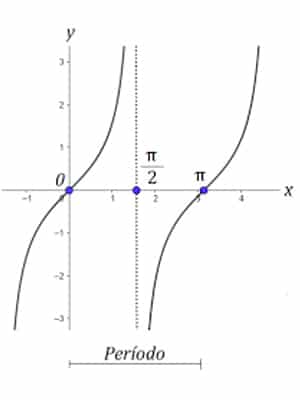
Portanto, dizemos que o período da função tangente é apenas π. 

Sendo assim, podemos reescrever qualquer valor da função como (x + πk). 

Como resolver funções trigonométricas?

Só precisamos de 4 passos para resolver uma função trigonométrica:

• Passo 1: Ler o enunciado (ou o gráfico) e interpretar a questão para saber se é seno ou cosseno;
• Passo 2: Escrever a lei da função;
• Passo 3: Identificar o problema e substituir seu valor na função;
• Passo 4: Resolver normalmente, lembrando do par ordenado.

Exemplo de exercício de funções trigonométricas (resolvido)

(Enem 2015)

Segundo o Instituto Brasileiro de Geografia e Estatística (IBGE), produtos sazonais são aqueles que apresentam ciclos bem definidos de produção, consumo e preço. Resumidamente, existem épocas do ano em que a sua disponibilidade nos mercados varejistas ora é escassa, com preços elevados, ora é abundante, com preços mais baixos, o que ocorre no mês de produção máxima da safra.

A partir de uma série histórica, observou-se que o preço P, em reais, do quilograma de um certo produto sazonal pode ser descrito pela função:

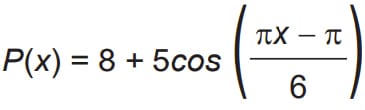
onde x representa o mês do ano, sendo x = 1 associado ao mês de janeiro, x = 2 ao mês de fevereiro, e assim sucessivamente, até x = 12 associado ao mês de dezembro.

Na safra, o mês de produção máxima desse produto é:

a) janeiro.

b) abril.

c) junho.

d) julho.

e) outubro.

Solução da função trigonométrica:

A questão pode parecer um monstro de sete cabeças, mas é mais simples do que aparenta! Veja só: 

Qual foi a pergunta central da questão? Ela perguntou qual era o mês de produção máxima. Mas a fórmula que foi dada é para calcular o preço. 

• O que fazer? Encontrar uma relação entre produção e preço!

De todo parágrafo inicial, o único dado que remete a algo matemático está no final: “com preços mais baixos, o que ocorre no mês de produção máxima da safra.”

Em outras palavras, ele está dizendo que no mês em que a produção é maior, o preço por unidade é menor. Então, concluímos que devemos calcular o preço mínimo para encontrar o mês de produção máxima.

• Como saber o preço mínimo? É aqui que entra a trigonometria!

A função trigonométrica que foi dada é função cosseno. Ora, nós acabamos de ver ao longo do artigo que os valores da função cosseno só podem variar de -1 a 1. Portanto, o preço mínimo é aquele dado por um cosseno que vale -1. 

O cosseno de quem vale -1? Claramente, é o cos180°! 

Isso significa que tudo o que está dentro do parêntesis precisa ser igual a 180°. Como as informações dentro do parêntesis estão em radiano, nós precisamos usar o 180° em radianos, que é igual a π rad.

Portanto:

cos ([π.x – π] / 6) = -1

(π.x – π) / 6 = π

π.x – π = 6π

π.x = 6π + π

π.x = 7π

x = 7

A questão disse que os valores de x equivale aos meses, sendo que 1 = Janeiro. Portanto, 7 = ao mês de Julho, o mês de produção máxima!

Quer revisar tudo o que aprendeu? Salva o Pin do Beduka que tem tudo resumidinho!

Gostou do nosso artigo sobre o que são funções trigonométricas? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.

Experimente agora!