A análise combinatória é a parte da matemática que estuda métodos que permitem resolver problemas relacionados ao princípio fundamental da contagem. Além disso, é uma das matérias que mais caem no ENEM. Resolva nossos exercícios e se prepare para essa prova tão importante.
A análise combinatória é um tema muito importante nas provas de matemática e que inclusive está presente no nosso artigo sobre os temas mais cobrados do ENEM. Nesse artigo iremos apresentar a definição e alguns exercícios sobre análise combinatória para que você chegue bem preparado no dia do vestibular escolhido.
O Beduka também possui outros conteúdos de matemática que te ajudarão na hora de estudar para o ENEM e outros vestibulares. Veja o que é triângulo isósceles, saiba como aprender geometria e saiba um pouco mais sobre trigonometria no triângulo retângulo.
Além dos exercícios sobre análise combinatória, preparamos para você um plano de estudos gratuito para que você possa se organizar para os vestibulares.
Você também pode testar os seus conhecimentos no nosso simulado. É grátis!
O que é Análise Combinatória?

Análise combinatória é a área da matemática que estuda a análise das possibilidades e combinações. É, basicamente, um conjunto de procedimentos que possibilita a construção de grupos diferentes formados por um número finito de elementos de um conjunto sob certas circunstâncias. Nesses grupos é possível realizar a análise das possibilidades e combinações.
Caso queira, por exemplo, saber quantos números de quatro algarismos são formados com os algarismos 0, 2, 3, 4, 5, 6, 7 e 9, pode se utilizar das propriedades da análise combinatória.
A análise combinatória se resume em 6 procedimentos principais:

- Fatorial
- Princípio fundamental da contagem
- Arranjos simples
- Permutação simples
- Combinação
- Permutação com elementos repetidos
Veja sobre cada um dos procedimentos a seguir.
1 – Fatorial
Considerando n como um número natural maior que 1, podemos definir como fatorial desse número n (n!) o número:
n! = n(n – 1)(n – 2)(n – 3)x…x3x2x1
Lê-se n! como n fatorial ou fatorial de n.
Aprenda um pouco mais sobre fatorial fazendo nossa lista de exercícios sobre o tema!
2 – Princípio Fundamental da Contagem
Quando um evento é composto por n etapas sucessivas e independentes, de tal forma que as possibilidades da primeira etapa é m e as possibilidades da segunda etapa é n, consideramos então que o número total de possibilidades de o evento ocorrer é dado pelo produto m*n.
3 – Arranjos Simples
Arranjos simples de n elementos tomados p a p (p ≤ n) são os diferentes agrupamentos ordenados que se podem formar com p dos n elementos dados.
Indica-se por An,p ou Anp o total desses agrupamentos, que calculamos assim:
An,p = n(n – 1)(n – 2) x…x(n – p + 1)
4 – Combinações Simples
Combinações simples de n elementos tomados p a p (p ≤ n) são os subconjuntos com exatamente p elementos que se podem formar com os n elementos dados.
Indica-se por Cn, p , Cnp o número total de combinações de n elementos tomados p a p
e calcula-se por Cn,p = n!
p! (n – p)
n é a quantidade de elementos de um conjunto
p é um número natural menor ou igual a n, que representa a quantidade de elementos que irão formar os agrupamentos.
5 – Permutações Simples
A permutação simples pode ser considerada como um caso particular de arranjo, onde os elementos formarão agrupamentos que se diferenciarão somente pela ordem. As permutações simples dos elementos P, Q e R são: PQR, PRQ, QPR, QRP, RPQ, RQP.
Para determinarmos o número de agrupamentos de uma permutação simples utilizamos a seguinte expressão
p = n!.
n! = nx(n-1)x(n-2)x(n-3)x…..x3x2x1
Por exemplo, 4! = 4x3x2x1 = 24
6 – Permutações de Elementos Repetidos
Permutação de elementos repetidos deve seguir uma forma diferente da permutação, pois elementos repetidos permutam entre si.
A permutação da palavra MATEMÁTICA ficaria da seguinte forma:
Sem levar em consideração as letras (elementos) repetidas, a permutação ficaria assim:
P10 = 10! = 3.628.800
Exercícios sobre Análise Combinatória
1. (ENEM) – O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.
Todos os alunos decidiram participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada.
O diretor sabe que algum aluno acertará a resposta porque há
a) 10 alunos a mais do que possíveis respostas distintas.
b) 20 alunos a mais do que possíveis respostas distintas.
c) 119 alunos a mais do que possíveis respostas distintas.
d) 260 alunos a mais do que possíveis respostas distintas.
e) 270 alunos a mais do que possíveis respostas distintas.
2. (Fuvest) – Três empresas devem ser contratadas para realizar quatro trabalhos distintos em um condomínio. Cada trabalho será atribuído a uma única empresa e todas elas devem ser contratadas. De quantas maneiras distintas podem ser distribuídos os trabalhos?
a) 12
b) 18
c) 36
d) 72
e) 108
3. (ENEM) – Como não são adeptos da prática de esportes, um grupo de amigos resolveu fazer um torneio de futebol utilizando videogame. Decidiram que cada jogador joga uma única vez com cada um dos outros jogadores. O campeão será aquele que conseguir o maior número de pontos. Observaram que o número de partidas jogadas depende do número de jogadores, como mostra o quadro:
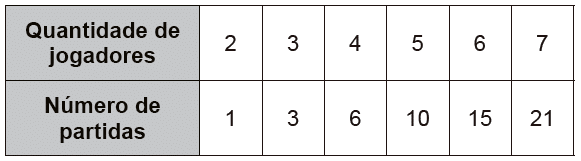
Se a quantidade de jogadores for 8, quantas partidas serão realizadas?
a) 64
b) 56
c) 49
d) 36
e) 28
4. (UFMG) – Um clube resolve fazer uma Semana de Cinema. Para isso, os organizadores escolhem sete filmes, que serão exibidos um por dia. Mas, ao elaborar a programação, eles decidem que três desses filmes, que são de ficção científica, devem ser exibidos em dias consecutivos. Nesse caso, o número de maneiras diferentes de fazer a programação dessa semana é:
a) 144
b) 575
c) 720
d) 1040
5. (ENEM) – Uma empresa construirá sua página na internet e espera atrair um público de aproximadamente um milhão de clientes. Para acessar essa página, será necessária uma senha com formato a ser definido pela empresa. Existem cinco opções de formato oferecidas pelo programador, descritas no quadro, em que “L” e “D” representam, respectivamente, letra maiúscula e dígito.
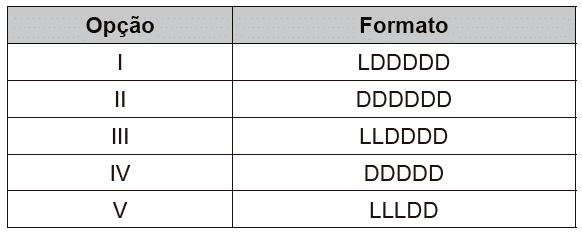
As letras do alfabeto, entre as 26 possíveis, bem como os dígitos, entre os 10 possíveis, podem se repetir em qualquer das opções.
A empresa quer escolher uma opção de formato cujo número de senhas distintas possíveis seja superior ao número esperado de clientes, mas que esse número não seja superior ao dobro do número esperado de clientes.
A opção que mais se adequa às condições da empresa é
a) I.
b) II.
c) III.
d) IV.
e) V.
6. (PUC-RJ) – A senha de acesso a um jogo de computador consiste em quatro caracteres alfabéticos ou numéricos, sendo o primeiro necessariamente alfabético. O número de senhas possíveis será então:
a) 364.
b) 10.36³.
c) 26.36³.
d) 264.
e) 10.264.
7. (Unesp) – O conselho administrativo de um sindicato é constituído por doze pessoas, das quais uma é o presidente deste conselho. A diretoria do sindicato tem quatro cargos a serem preenchidos por membros do conselho, sendo que o presidente da diretoria e do conselho não devem ser a mesma pessoa. De quantas maneiras diferentes esta diretoria poderá ser formada?
a) 40.
b) 7920.
c) 10890.
d) 11!.
e) 12!.
Aprenda muito mais com o Beduka
Siga o Beduka no Instagram para não perder as novidades!
Abaixo apresentamos mais exercícios resolvidos nos quais você pode se aprofundar mais:
O Beduka é um buscador gratuito de cursos e faculdades, particulares ou públicas, que surgiu em 2017. Através de uma pesquisa simples você encontra informações detalhadas sobre todas as instituições de ensino superior registradas no Ministério da Educação (MEC). Experimente agora!
Agora que você conferiu alguns exercícios sobre análise combinatória, aproveite e veja outros artigos que podem te ajudar no ENEM e em outros vestibulares. Saiba a definição de movimento uniforme, veja quais são os pronomes interrogativos e estude um pouco mais sobre a chuva ácida.
Gabarito dos Exercícios sobre Análise Combinatória
Exercício resolvido da questão 1 – a
Exercício resolvido da questão 2 – c
Exercício resolvido da questão 3 – e
Exercício resolvido da questão 4 – c
Exercício resolvido da questão 5 – e
Exercício resolvido da questão 6 – c
Exercício resolvido da questão 7 – c
Gostou dos nossos exercícios sobre análise combinatória? Compartilhe com os seus amigos e comente abaixo sobre áreas que você deseja mais explicações.
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





