Os 5 passos para aprender a Interpretação de problemas matemáticos!

Pode parecer “a maior viagem”, mas a interpretação é uma arte! Sabe porque? A palavra “arte” significa “técnica” e é preciso ter habilidades específicas para fazer a interpretação de problemas matemáticos … E isso explica porque muitos alunos acham as questões tão confusas! Mas nós vamos te ajudar a descomplicar, mostrando dicas e exemplos resolvidos. 

Neste resumo, você encontrará os tópicos abaixo. Se quiser, clique em um deles para ir diretamente ao conteúdo:

1. O que é a interpretação de problemas matemáticos?
2. Conheça as partes do enunciado para entendê-lo!
3. Como interpretar as questões de matemática?
4. Aprenda os 5 Passos para interpretar problemas matemáticos!
5. Exemplo de problema resolvido!

Organize seu tempo de estudos com o Plano de Estudos Beduka! É gratuito e você conseguirá encaixar uma rotina de estudo eficaz junto aos demais afazeres. 

O que é a interpretação de problemas matemáticos?

Uma boa palavra para definir a interpretação é “tradução”. Interpretar é traduzir a linguagem da questão, que nesse caso é matemática, para o português. E vice-versa! 

Essa ponte entre símbolos e códigos cria a comunicação efetiva. Ela faz nosso cérebro entender a mensagem e sermos capazes de respondê-la no mesmo formato!

Na hora de resolver exercícios, saber as fórmulas é importantíssimo, mas não se resume somente a isso… Apenas a interpretação faz com que nossa cabeça saiba a hora certa de usar a fórmula e com quais informações.

Portanto, o sucesso na solução de problemas está ligado à habilidade (arte) de enxergar a ligação das palavras do português com a sua representação na matemática.

Sim, é preciso ser bom de português para ser bom de matemática. E tem gente achando que exatas não se mistura com linguagens…

E dizemos mais: não importa muito se você é de humanas, biológicas, ou qualquer outra coisa. Saber a interpretação dos problemas matemáticos é uma dificuldade comum a todos.

Porém, é essencial não se acomodar e sempre buscar se superar. Essa habilidade é essencial para a sua vida e te ajuda a desenvolver o raciocínio lógico. Fora que sempre cai nas provas dos vestibulares e concursos… 

Nós até já fizemos um texto contando qual a melhor maneira de estudar matemática! 

Agora, vamos voltar ao que interessa e continuar trabalhando na nossa arte:

Conheça as partes do enunciado para entendê-lo!

Você já entendeu que vamos fazer algo literalmente artístico aqui, já que precisamos de muita habilidade para interpretar as questões! 

(Não é atoa que chamamos de problemas matemáticos, hahaha)

Porém, a técnica é a parte prática da coisa. Ela é a ação que vamos fazer ao se deparar com uma questão. E nós só dominamos aquilo que conhecemos…. 

Então, a primeira coisa que precisamos fazer é conhecer os elementos de um enunciado. Depois saberemos o que fazer com ele!

Vamos analisar os seus 4 componentes:

1. A situação-problema

Como o próprio nome diz, a situação-problema é o contexto que estamos lidando. Ele narra qual é o fato que aconteceu e que levou o problema a ser resolvido.

Basicamente, existem dois tipos de problemas:

• Problemas de determinação: precisamos descobrir a informação que falta.
• Problemas de demonstração: temos de mostrar que uma afirmativa da matemática é verdadeira.

Tendo como referência a seguinte questão…

“O perímetro de um triângulo retângulo é 12 cm. As medidas de seus lados são números consecutivos. Qual é a medida da área dessa figura?”

Já sabemos que se trata de um problema de determinação, afinal, o contexto é encontrar algo que falta de um triângulo.

• São mais de 200 resumos gratuitos no Instagram do Beduka. Aproveite!

2. Os dados

Os dados são justamente as informações que usamos na hora de resolver o problema. Essas informações podem ser números ou palavras, podem estar explícitas ou implícitas.

Observe a nossa questão de referência:

“O perímetro de um triângulo retângulo é 12 cm. As medidas de seus lados são números consecutivos. Qual é a medida da área dessa figura?”

Os dados que conseguimos retirar dela são:

• 12 cm é o valor do perímetro (explícito);
• As medidas dos lados são números consecutivos (explícito);
• Um triângulo tem três lados (implícito);
• Perímetro é a soma das medidas dos lados (implícito).

3. O Objetivo

Como você já sabe, o objetivo é onde queremos chegar. Ele é aquilo que procuramos e, quando acharmos, será dado como resposta da questão. 

Releia a nossa questão de referência:

“O perímetro de um triângulo retângulo é 12 cm. As medidas de seus lados são números consecutivos. Qual é a medida da área dessa figura?”

O objetivo está bem claro: devemos encontrar a área do triângulo que tem as características anteriores.

Esse foi fácil né? Mas alguns alunos se perdem bem nessa parte. 

Sempre destaque no enunciado qual é o objetivo para conferir se a resposta encontrada tem a ver. Às vezes, a questão é longa e tem duas partes. Você termina a primeira e vê o resultado na alternativa… acaba marcando e erra!

4. As operações

As operações são as ações matemáticas que faremos para resolver a questão. São nelas que usamos os dados e calculamos o que precisamos.

Aqui também é uma etapa essencial, pois precisamos identificar quais operações são necessárias em cada situação-problema. Esse é o caminho para o sucesso!

Vamos voltar uma última vez ao nosso problema de referência:

“O perímetro de um triângulo retângulo é 12 cm. As medidas de seus lados são números consecutivos. Qual é a medida da área dessa figura?”

Se o objetivo é achar a área, nós precisamos usar a fórmula da área de um triângulo. Mas essa não é a primeira operação que faremos, e sim a última. 

Isso porque precisamos dos valores dos lados para jogar na fórmula. Então, nossa primeira operação será achar os lados do triângulo…

E é aqui que entra a estrela da noite: a interpretação de texto! Agora, vamos dar um pause para ver umas dicas que nos apontam a “tradução”. Depois ficará mais fácil encontrar o valor desses lados.

• Faça o nosso Simulado ENEM gratuito! Personalize com as matérias que você quiser.

Como interpretar as questões de matemática?

Já te contamos que o segredo da interpretação de problemas matemáticos é fazer a tradução. É como se estivéssemos aprendendo uma outra língua.

Com base nisso, separamos algumas dicas para te ajudar a entender as palavras que indicam operações. Observe:

Como identificar a Divisão?

Quando a preposição “por”  estiver entre duas quantidades, ela representará uma divisão. Há outros termos que são comuns, como: “razão” ou “quociente“.  Mas algumas questões vêm falando claramente: “Fulana dividiu tantas coisas entre tais cicranos”.

Note que o nome porcentagem significa “por cento”. Então dividir por 100 é uma dica para transformar uma porcentagem em fração.

Como identificar a Multiplicação?

A preposição “de” e as contrações “da“, “do“, “dessa” e “desse” costumam indicar que precisaremos de uma multiplicação, principalmente se estiverem entre duas quantidades. Isso acontece muito nas questões de Porcentagem.

Exemplo: 

A pizza que a família Barros pediu tinha 8 fatias. Mas só havia 62,5% da pizza em cima da mesa, porque Juninho tinha comido algumas fatias antes de todos. Qual foi a quantidade que ele comeu?

Solução:

Se havia 62,5% e o total era 100%, então juninho comeu 37,5%. Essa porcentagem equivale à fração 37,5/100, que equivale ao número 0,375. Neste formato de decimal, fica mais fácil multiplicar pelo total de 8 fatias. Aí descobrimos que Juninho comeu 3 fatias!

Atenção!

Na matéria de Probabilidade, a partícula “e” entre eventos é quem dá a dica de que precisamos multiplicar os resultados. Porém, se houver a partícula “ou”, indicará a operação de soma.

Exemplo: 

No verão da cidade de Claraval, a previsão do tempo disse que há 30% de chance de chover. E se não chover, há 20% de chance de ficar nublado. Qual é a chance final e total de não ficar nublado?

Solução:

Se havia 30% de chance para chuva, então havia 70% de não chover. Uma vez que não choveu, há 20% de ficar nublado e, portanto, 80% de não ficar nublado. Observe: a chance total e final de não ficar nublado depende de não chover e não nublar ao mesmo tempo.

Portanto, é dada pela expressão: 70% x 80% = 56%.

Como saber quem é a Incógnita?

A incógnita, também chamada de variável, é o valor que não conhecemos.  Normalmente, ele é representado por letras.

É interessante perceber que as incógnitas podem ou não representar o nosso objetivo. Há questões em que terão duas incógnitas, sendo uma o objetivo e a outra um elemento que faltava para alcançar o objetivo. 

Também há questões em que só há uma operação para ser feita, então o uso de incógnita é opcional.

De modo geral, a presença dela pode ser identificada pelas palavras: qual, que, certo valor, certa quantia, quantos, …

• Saber interpretar gráficos também é essencial!

O dobro, a metade, o sucessor, o inverso…

Essas palavras costumam aparecer em problemas de lógica sem nenhum valor explicitamente associado. 

E é nessa hora que a gente se embaralha todo! Mas é mais simples do que aparenta, basta usar as incógnitas para traduzir as palavras. 

Veja só:

• O dobro (2) de (multiplica) um valor qualquer (x) = 2x
• O triplo de um valor = 3y
• A metade (½) de um valor = x/2
• A terça parte de um valor = y/3
• O sucessor de um número = x+1
• O antecessor de um número = x-1
• O inverso de uma quantia = 1/y

Identificando a Igualdade (equação)

Quando os verbos “é”, “possui”, “tem” e “equivale” estão entre duas quantidades, eles nos apontam para uma equação. Elas podem envolver incógnitas ou não, estando explícitas ou implícitas.

Exemplo: 

Ruth e Raquel juntaram suas economias e compraram 50 balas, sabendo que cada bala custava R$ 00,20. Se Ruth tivesse o dobro de seu valor e Raquel tivesse a terça parte, elas ainda poderiam comprar a mesma quantia de balas. Quantos reais tinham cada uma delas?

Solução:

Vamos supor que Ruth tinha x reais e Raquel tinha y. Quando elas compraram 50 balas valendo vinte centavos cada, então elas tiveram um gasto de 10 reais. Com base nisso, podemos escrever a primeira informação como x + y = 10.

Depois, o enunciado supõe novos valores. O dobro para Ruth (2x) e a terça parte para Raquel (y/3). Mesmo com esses valores, elas podem comprar a mesma quantia de balas, então terão o mesmo gasto. Temos uma nova equação: 2x + y/3 = 10.

Quando estamos diante de duas equações com as mesmas duas incógnitas, só podemos usar os sistemas de equações para resolver!

Usando o método da substituição, temos que: 

Se x = 10 – y

Então 2(10-y) + y/3 = 10

20 – 2y + y/3 = 10

60 – 6y + y = 30

60 – 30 = 6y – y

30 = 5y

y = 6 (quantia de Raquel)

Se x = 10 – y

Então x = 10 – 6

x = 4 (quantia de Ruth)

Quais são os 5 Passos para fazer a interpretação de problemas matemáticos?

Bom, agora que já entendemos todos os elementos do enunciado e as estratégias de interpretação, podemos listar quais são as etapas para fazer uma boa interpretação de texto. 

Veja só:

• 1º Passo: leia o problema uma vez, para entender o que está acontecendo na situação-problema
• 2º Passo: Leia novamente, anotando ou marcando o que é dado explícito, implícito, objetivo e as palavras que indicam operações.
• 3° Passo: Olhe para as anotações, veja quais operações podem ser feitas e quantas etapas precisará para isso (interpretação). Trace seu raciocínio.
• 4° Passo (opcional): se possível, faça um desenho para te ajudar a visualizar e organizar as informações.
• 5° Passo: resolva todas as etapas e veja se o resultado final corresponde ao objetivo.

Retomando e finalizando o nosso exemplo!

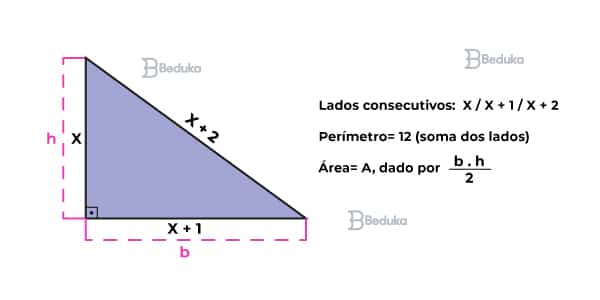
Lembra daquele exemplo lá no início, que usamos para identificar os elementos da equação? Vamos vencê-lo de uma vez por todas!

“O perímetro de um triângulo retângulo é 12 cm. As medidas de seus lados são números consecutivos. Qual é a medida da área dessa figura?”

Os dois primeiros passos nós já fizemos lá em cima, agora só nos resta terminar os outros 3.

Solução:

Vamos chamar de “x” o lado menor do triângulo. Se os lados são números consecutivos, então o lado mediano é “x+1” e o lado maior é “x+2”. 

Sabemos que perímetro é a soma dos lados, então x + x+1 + x+2 = 12. Resolvendo a equação, temos: 

3x + 3 = 12

3x = 9 

x = 3 cm

Note que 3 é o valor do lado menor, então o outro mede 4 e o maior mede 5. Se foi dito que é um triângulo retângulo, então 5 é a hipotenusa. Logo, os valores que sobram para os catetos são 3 e 4.

Aqui não importa saber a ordem em que eles estão, o importante é notar que eles serão base e altura do triângulo, justamente o que precisamos para usar a fórmula de área!

Chamando a área de “A” e aplicando a fórmula (b.h) / 2, temos: 

A = (3.4) / 2  

A = 12 / 2

A = 6 cm²

Agora sim resolvemos o problema: o valor de sua área é 6!

Gostou do nosso resumo sobre a interpretação de problemas matemáticos? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.

Experimente agora!