Plano Cartesiano: o que é, elementos, cálculo e importância!

O Plano Cartesiano é uma ferramenta matemática gráfica, ou seja, desenhada com duas dimensões. Ele é formado por duas retas numéricas perpendiculares: na vertical, Y ou Ordenadas e na horizontal, X ou Abscissas. O plano é utilizado para a localização de pontos do sistema de coordenadas, importante para geometria, geografia e outras áreas.

Neste artigo sobre Plano Cartesiano, você encontrará:

1. O que é Plano Cartesiano? Exemplo e Importância
2. Elementos do plano – Como formá-lo e os quadrantes
3. Sistema de coordenadas e como calcular 
4. Curiosidade ao final

• Depois de ler o artigo, treine com os exercícios de plano cartesiano!
• Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!

O que é Plano Cartesiano? Exemplo

O plano cartesiano é uma ferramenta matemática gráfica (desenhada). É como um objeto ou método para realizar operações ao analisar sua imagem: um plano de duas dimensões (altura e largura) marcado com duas retas cheias de números. 

Adiante, detalharemos os elementos desse plano, mas agora você só precisa ter o básico para entender do que estamos falando. Você já deve ter visto algo semelhante por aí. Se não, no próximo tópico teremos exemplos em imagens!

O plano cartesiano tem esse nome porque foi criado pelo filósofo e matemático René Descartes. Este pensador nasceu no início da Idade Moderna, em um meio Renascentista, onde o Iluminismo ganhava força. 

Tudo isso quer dizer que o principal ideal humano da época era a razão e a lógica. Por isso, a matemática foi potencializada e sempre buscava-se uma explicação racional e sistematizada para tudo.

Qual é a utilidade do Plano Cartesiano?

Por se tratar de uma ferramenta matemática, sua aplicação é muito ampla e sempre tem o objetivo de auxiliar a resolver problemas.

Sua principal aplicação é para a localização de elementos em um espaço, principalmente os espaços bidimensionais como é o plano.

Algumas das áreas da ciência que podem utilizar esse recurso são: 

• Geometria (plana, espacial e analítica)
• Trigonometria
• Astronomia
• Cartografia
• Física vetorial
• Arqueologia
• Engenharia
• Design
• Forças táticas e militares
• GPS e Navegação (aérea, terrestre e marítima)

Essa teorização de posições e a mistura com diversas áreas das funções humanas, permitiu a demonstração de ideias ainda não testadas na prática. Assim, o processo de aprimoramento das tecnologias, construções e operações foi mais rápido e seguro.

Elementos do Plano Cartesiano – Como ele é formado?

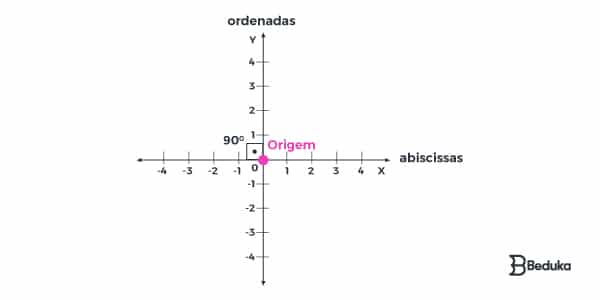
O plano cartesiano é formado por duas retas perpendiculares entre si, ou seja, formam um ângulo de 90° (reto). Elas precisam ser retas numéricas, cheias de números reais equidistantes (mesmo espaçamento entre si), como uma régua. 

• Uma das retas está no sentido vertical, esse eixo é chamado de ordenadas e costuma ser representado pela letra “Y”. 

• A outra reta está no sentido horizontal, esse eixo é chamado de abscissas e costuma ser representado pela letra “X”.

Essas retas só se encontram em um único ponto, chamado de Origem. Ele é o “marco 0” de ambas as retas. Também é o ponto central pois consideramos os valores negativos (à esquerda ou abaixo) e os positivos (à direita ou acima).

Cada ponto na reta está ligado a somente um número real. Como os números são infinitos, as retas também são. Porém, só representamos aqueles que dizem respeito ao contexto da situação que estamos.

Só assim teremos a garantia de que é possível medir, posicionar e localizar as coisas de forma correta.

Alguns planos têm uma malha quadriculada ao fundo, esse não é um elemento obrigatório, mas serve para facilitar a localização dos pontos fora da reta. Veremos como isso funciona nos tópicos à frente!

O que é o sistema de coordenadas cartesianas?

Sistema de coordenadas é o nome do esquema de identificação de pontos no plano cartesiano. Como há 2 eixos, sempre precisamos dar a posição de um ponto em relação às duas retas.

Por isso, o que caracteriza o sistema de coordenadas é o par ordenado. Funciona da seguinte maneira:

Ele é sinalizado entre parênteses e com uma vírgula no meio. A vírgula tem função de separar o primeiro membro e o segundo, os parênteses servem para mostrar que toda aquela informação pertence a um mesmo ponto.

• No primeiro membro temos um número real que é a posição do ponto em relação ao eixo X, ou seja, às abscissas.

• No segundo membro temos um número real que é a posição do ponto em relação ao eixo Y, ou seja, às ordenadas.

Exemplo: H (-2 , 4) 

Significa que o ponto H está localizado na posição -2 em relação ao eixo X e, ao mesmo tempo, na posição 4 em relação ao eixo Y.

• Genericamente, um par ordenado pode ser representado por (X,Y) e o ponto de Origem sempre é (0,0).

Como calcular as coordenadas de um ponto?

Existem diversas formas de calcular as coordenadas de um ponto. Todas aquelas que envolvem álgebra, fórmulas e contas complexas são matéria da geometria analítica ou trigonometria, como a distância entre dois pontos, ponto médio, etc.

Porém, a matéria aqui não é essa, mas sim entender como funciona o plano e o sistema de coordenadas. Então, vamos entender como fazer a identificação:

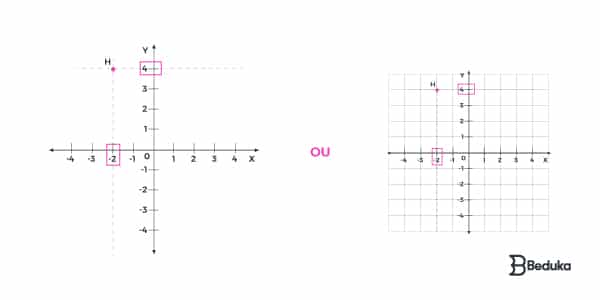
Vamos retomar o ponto H (-2 , 4) .

• Primeiro, devemos traçar uma linha vertical sobre o número do eixo das abcissas (X). Isso porque o ponto pode estar em qualquer área que o número X “enxergue”. Ou seja, pode estar acima ou abaixo, mas sempre alinhado com ele.

• Depois, desenhamos uma linha horizontal sobre o número do eixo das ordenadas (Y). Isso porque o ponto pode estar em qualquer área que o número “enxergue”. Ou seja, pode estar em qualquer um de seus lados, mas sempre alinhado com ele.

• Porém, como se trata de um par, é necessário que ambas as condições de posição sejam satisfeitas. Por isso, o ponto H é o encontro dos prolongamentos dos números da reta.

Alguns planos cartesianos já vêm desenhados com a malha quadriculada ao fundo para que você não tenha o trabalho de prolongar. Com isso, você já pode bater o olho e identificar onde está o ponto!

Quais são os Quadrantes do Plano Cartesiano?

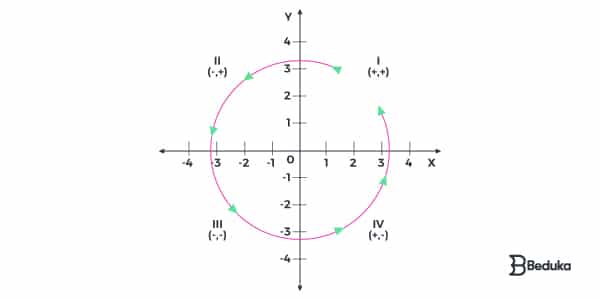
Quadrante vem da palavra “quatro”, ou seja, são quatro áreas divididas que existem no plano cartesiano. Por isso, os nomes são: 1° quadrante, 2° quadrante, 3° quadrante e 4° quadrante. 

• Fazemos a leitura da ordem dos quadrantes em sentido anti-horário!

Como há duas retas que se cruzam perpendicularmente, essas áreas divididas formadas são todas proporcionais e simétricas. Comparando duas a duas podem ser espelhadas e opostas.

Além disso, como trata-se de uma reta numérica e o centro é o ponto de origem, podemos classificar os quadrantes também quanto ao sinal dos números alí presentes (negativos ou positivos). Veja:

• 1° Quadrante (I): retas x e y têm valores positivos (x > 0 e y > 0) ou (x, y)
• 2° Quadrante (II): reta x com valores negativos e reta y com positivos (x < 0 e y > 0) ou (-x, y)
• 3° Quadrante (III): retas x e y têm valores negativos (x < 0 e y < 0) ou (-x, -y)
• 4° Quadrante (IV): reta x com valores positivos e reta y com negativos (x > 0 e y < 0) ou (x, -y)

Curiosidade: Plano de três dimensões

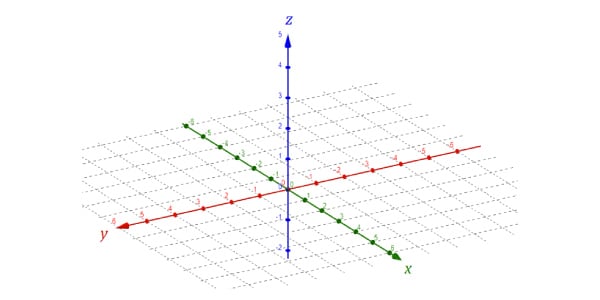
No plano cartesiano nós trabalhamos quase sempre com figuras planas, ou seja, aquelas da geometria plana e que só possuem duas dimensões (altura e largura). 

Porém, o desenvolvimento da geometria espacial fez com que houvesse a necessidade de representar figuras geométricas também. Assim, o Plano Cartesiano foi a base para criação de um novo plano tridimensional (altura, largura e profundidade).

Para isso, é necessário que um novo eixo apareça, o eixo “Z”. Ele é perpendicular a todo o plano cartesiano (x, y). É como se as ordenadas e abscissas estivessem desenhadas em uma folha deitada e atravessarmos um palito verticalmente.

Ele também é uma reta real e o seu marco zero é coincidente com a origem. As consequências numéricas disso só aparecerão nos cálculos da geometria analítica. Além disso, é preciso desenvolver a visão espacial para entender os desenhos!

Gostou do nosso artigo sobre o Plano Cartesiano? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!

Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.

Experimente agora!