Função Logarítmica é toda aquela que possui um logaritmo na expressão matemática, ou seja, que é do tipo f(x) = loga x. Ela também deve obedecer à condição de existência a > 0 e a ≠ 1. Seu gráfico é o oposto da função exponencial.
Neste artigo sobre Função Logarítmica, você encontrará:
- O que é Função logarítmica (definição e exemplos)
- Domínio e Imagem
- Como resolver
- Como fazer e interpretar o gráfico
- Estudando para as provas? Conheça O melhor Simulado do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!
O que é função Logarítmica? (definição e exemplos)
Uma função logarítmica é toda aquela que possuir um logaritmo na sua lei de formação. Por isso, ela sempre será baseada no seguinte formato:
f(x) = loga x
Além de ter essa lei de formação, é preciso que siga as condições de existência (CE): a ≠ 1 e a > 0. Em outras palavras, o número que ocupar o lugar de “a” deve ser positivo (a > 0) e diferente de 1 (a ≠ 1) ao mesmo tempo.
Se apresentar tudo isso, poderá ser classificada como função logarítmica de base a.
O motivo é que o Log é usado para descobrir o valor do expoente de uma base dada, então é a operação inversa da exponenciação. Já que eles têm propriedades bem específicas, não funcionam (deixam de existir) quando temos um a = 1 ou negativo.
É bom que você dê uma lida nesses dois artigos antes de continuarmos!
Exemplos de funções com Log
- f(x) = log3 x
- g(x) = log⅓ x + 6
- h(x) = log10 x (é o mesmo que log x)
- Y = log5 (x-2)
Esqueceu o que é uma função matemática?
Você pode ler o artigo completo, mas já te adiantamos um resumo:
As funções são expressões numéricas que seguem um padrão. São regras que relacionam dois valores (x e y). Esses valores são as incógnitas, e elas são dependentes entre si.
Isso significa que o y se modifica à medida que mudamos o valor de x. Quando usamos a expressão “f(x)” referimo-nos ao valor final daquela função quando colocamos o valor de x nela. Então Y = f(x).
Por isso, devemos resolver as funções pensando nos pares ordenados (x,y) que se adequam àquela regra.
Para que serve a Função Logarítmica?
A função logarítmica é útil para situações as mesmas situações que envolvem funções exponenciais, mas seu uso se faz necessário quando já temos a base e só precisamos do expoente ou do valor final da função.
Então, ele é muito usado nas situações de juros compostos, na geografia para medição da magnitude de terremotos, na química para realizar experimentos, na biologia para o cálculo de crescimento das populações e por aí vai!
Além disso, sempre aparece ao menos uma questão desse assunto no Enem e nos demais vestibulares!
Domínio e Imagem de uma Função Logarítmica
Todos os possíveis valores para x são agrupados no conjunto chamado domínio (D). Da mesma forma, todos os possíveis valores para y são agrupados no contradomínio (CD).
Os valores do CD que foram usados como resultado da função, são do conjunto Imagem (I).
Se lembrarmos das condições de existência da Função Logarítmica, podemos dizer que o domínio é representado pelo conjunto dos números reais positivos. Então não incluem o zero nem os valores negativos (R*+).
Já o contradomínio e imagem pode ser qualquer valor, então é representado pelo conjunto dos números reais.
- Exemplo:
Determine o domínio da função: f(x) = log2 2x+1
A resolução é simples, só precisamos tomar cuidado com a condição de existência do logaritmo, que é a > 0 e a ≠ 1.
Então:
2x + 1 > 0
2x > -1
x > –1⁄2
Logo, o domínio (todos os valores que x pode assumir) dessa função é definido assim:
D = {x ∈ R | x > –1⁄2 }
Como resolver uma Função Logarítmica? (Exemplo em 3 passos)
Para resolver uma função logarítmica, basta de seguir 3 passos:
- 1°Passo: substituia as informações dadas. Leia atentamente a questão e, se ela te der o valor de x, substitua o número nos lugares que tem x. Se te der o valor de y, coloque no f(x) e iguale à toda a expressão.
- 2°Passo: transforme em uma equação. Para isso, basta retirar o “f(x)” e substituir por y.
- 3°Passo: resolva normalmente, lembrando-se das propriedades dos logaritmos.
Exemplo:
Seja uma função f:*+ R → R, definida por f(x) = log2 (x+2), calcule f(2) e f(6).
- Resolução de f(2) para f(x) = log2 (x+2)
1°Passo: substituia as informações dadas.
f(2) = log2 (2+2)
f(6) = log2 (6+2)
2°Passo: transforme em uma equação
y = log2 (2+2)
y = log2 (6+2)
3°Passo: resolva normalmente.
y = log2 (2+2)
y = log2 (4)
2y = 4 (aplicando a definição de log)
Se 2 elevado a algo é =4, então só podemos estar falando de 2².
Logo, y = 2.
- Resolução de f(6) para f(x) = log2 (x+2)
y = log2 (6+2)
y = log2 (8)
2y = 8 (aplicando a definição de log)
Se 2 elevado a algo é = 8, então só podemos estar falando de 2³.
Logo, y = 3.
- Você é uma daquelas pessoas que tem fome de conhecimento? Então siga o Beduka no Instagram para conteúdos diários.
Como fazer o gráfico de uma Função Logarítmica? (4 passos)
Para construir e interpretar um gráfico de função logarítmica, você precisa lembrar que uma função é caracterizada pelos valores do par ordenado (x e y). Também precisamos lembrar como posicioná los no plano cartesiano.
Como uma função tem uma possibilidade de combinações infinitas e segue uma regra que a delimita, basta que você:
- 1° Passo: Estipule valores aleatórios para X ou Y(priorize valores pequenos, como -2,-1,0,1,2).
- 2° Passo: Calcule o resultado de Y para cada x que você usar na função. Se escolheu um valor para Y, calcule o x que torna a equação válida l.
- 3° Passo: Marque os pares ordenados no plano.
- 4° Passo: Ligue os pontos e o gráfico estará construído!
Mas lembre-se:
Todo gráfico de função exponencial é uma como uma hipérbole (curvilínea e cresce muito em menos tempo), só que é o inverso do gráfico da exponencial.
Além disso, podemos ver pelos gráficos se a função é crescente ou decrescente, de acordo com o desenho. Resumindo, podemos afirmar que a função logarítmica é:
- Injetora e Sobrejetora
- Crescente, para a > 1
- Decrescente, para 0 < a < 1
Vamos ver exemplos, cálculos e análises:
Função Logarítmica Crescente
Uma função logarítmica que tem base a > 1 é sempre crescente!
Observe a construção do gráfico da função f(x) = log2 x!

Com esses valores em mãos vamos construir o gráfico.
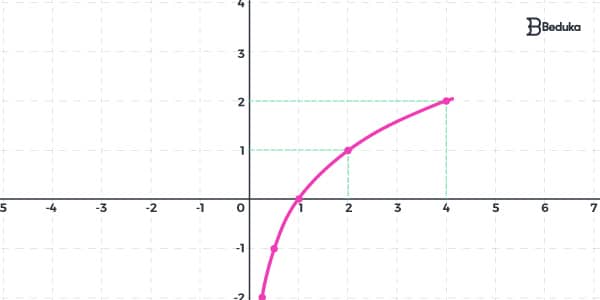
Veja que temos um gráfico crescente (se aumentarmos o valor de x, o valor de y aumentará também).
Ainda podemos notar que ele cresce mais lentamente ao longo do tempo.
Função Logarítmica Decrescente
Uma função logarítmica que tem base 0 < a < 1 é sempre decrescente!
Observe a construção do gráfico da função f(x) = log1⁄2 x!

Colocando esses valores no gráfico, temos:
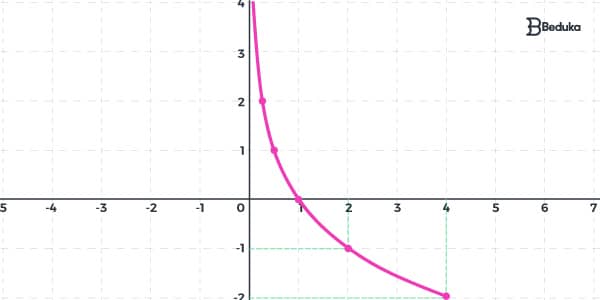
Veja que temos um gráfico crescente (aumentamos o valor de x e o y aumenta também).
Ainda podemos notar que ele decresce mais lentamente ao longo do tempo.
Gostou do nosso artigo sobre Função Logarítmica? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





