A Equação Exponencial é uma expressão numérica que possui ao menos uma incógnita no expoente. Isso significa que a variável (“x”, “y”, etc.) forma uma potência com a base numérica. Como toda equação, há um sinal de igualdade que relaciona os dois termos e por ser exponencial, segue à condição de existência: base positiva e diferente de 1.
Neste artigo, você encontrará:
- Introdução: O que é Equação e diferença de Função
- O que é Equação Exponencial
- Como resolver uma Equação Exponencial – passo a passo e propriedades
- Exemplos e sugestões de exercícios (com raiz, fração e bases diferentes)
- Estudando para as provas? Conheça nosso Simulado gratuito, que pode ser personalizado com as matérias que você mais precisa!
Introdução: o que é uma Equação
Antes de tudo, precisamos entender o que é Equação para continuarmos! Se você já sabe, pule para o próximo tópico!
A palavra “Equação” está originalmente relacionada à palavra igualdade. Uma Equação é uma expressão numérica e algébrica (números e letras) que possui dois lados: um que está antes do sinal de igual e outro depois. Portanto, falar em equação é querer tornar as coisas iguais, ou seja, igualar os lados.
Nesta igualdade há números conhecidos e outros desconhecidos. O valor que não sabemos é chamado de incógnita e ele pode ser representado por qualquer letra, o mais comum é utilizarmos “x”,”y”ou “z”.
A nossa missão é descobrir quanto vale a letra e essas equações podem ser de vários tipos: 1° grau, 2° grau, exponencial, etc.
Qual a diferença entre Equação e Função
As equações podem ser transformadas em função! Não é atoa que resolvemos as funções como equações! Ex: Função Exponencial, Função 1° grau, Função 2° grau, etc.
Ser uma função significa ter dependência, ou seja, o valor da função (y) se modifica à medida que modificamos o valor de x, pois o resultado depende da conta que é feito com o outro número. Um determinado valor de x produzirá um valor de y, logo, devemos resolver as funções pensando nos pares ordenados (x,y).
Dessa forma, uma equação só precisa ser resolvida para descobrir o valor de x e tornar a igualdade verdadeira. Já a função é variável, o todo da conta (a função, o valor y) muda de acordo com cada valor de x que for possível colocar.
O que é Equação Exponencial
A Equação Exponencial é aquela que possui ao menos uma incógnita no expoente. Isso significa que a variável “x” forma uma potência com a base numérica. Essa fórmula algébrica foi desenvolvida pelo matemático francês René Descartes, no século XVII, representando um grande avanço científico para a época.
Foi um avanço porque ele havia incluído as potências nas equações, ajudando a solucionar problemas de grande escala. Para entender melhor, confira nossa matéria sobre Potenciação! Ela é essencial para compreender esse tipo de equação.
Por este motivo, a equação exponencial segue algumas condições de existências, como a de que sua base deve ser positiva e diferente de 1.
Exemplos:
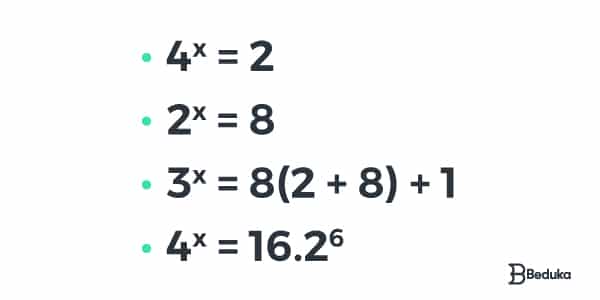
Como resolver uma Equação Exponencial – passo a passo e propriedades
O objetivo de resolver uma equação é descobrir quanto vale o “x”, ou seja, encontrar o valor da incógnita que torna a igualdade verdadeira. Para isso, devemos isolar os elementos desconhecidos no primeiro membro e colocar os valores conhecidos no segundo membro.
O passo a passo de toda equação é o mesmo, mas o modo como resolvemos as Exponenciais tem um detalhe a mais: precisamos igualar as bases para aplicarmos as propriedades de potenciação.
Veja o Passo a Passo:
- 1.Eliminar os parênteses fazendo as operações prioritárias
Algumas expressões podem estar escritas dentro de símbolos, como os parênteses ( ) , os colchetes [ ] e as chaves { }. Eles indicam a ordem: 1° resolvemos o que está dentro dos parênteses, 2° o que está dentro dos colchetes e 3° o que está dentro das chaves.
Se for impossível continuar resolvendo o que está em 1° lugar de prioridade, pulamos para o próximo passo. Apenas depois disso podemos resolver o que está fora.
Uma vez que identificamos as prioridades, podemos efetuar as operações. Elas também têm uma ordem: 1º potenciação e radiciação; 2º multiplicação e divisão e 3º soma e subtração.
Se existir mais de uma operação com a mesma prioridade, elas serão resolvidas da esquerda para direita.
Para igualar as bases das potências e podermos aplicar as propriedades, devemos fazer a fatoração. Fatorar significa decompor o número em fatores primos, isto é, escrever o número através de uma multiplicação de fatores iguais utilizando as regras de potenciação.
- 2. Efetuar a transposição de termos
Após isso, para podermos trocar os termos e organizá-los em cada membro, devemos mudar o sinal que ele carregava para o seu oposto:
Aquilo que está negativo passa como positivo e vice-versa
O que está multiplicando passa dividindo e vice-versa
Se havia raiz quadrada, passa como potência de expoente ½ e vice-versa
Atenção:
Ao passar as incógnitas de lado, devemos mantê-las juntas aos seus coeficientes e, neste caso, à base em que está.
- 3. Reduzir os termos semelhantes
Depois disso, efetuamos as operações entre os termos semelhantes (número com número, letra com letra).
- 4. Isolar a incógnita e encontrar seu valor numérico
Ao final, restará uma potência com sua incógnita no expoente. Quando não há mais nada a ser feito, aí aplicamos novas propriedades para descobrir o valor de “X”.
Exemplos e sugestão de exercícios
Veja abaixo a resolução das 4 equações que colocamos de exemplo aí acima! Depois, sugerimos que você treine com alguns exercícios de vestibulares sobre equação exponencial!
- Resolução da primeira equação do exemplo:

- Resolução da segunda equação do exemplo:

- Resolução da terceira equação do exemplo:

- Resolução da quarta equação do exemplo:

Equação exponencial com raiz
Uma equação com raiz quadrada se resolve da mesma forma que as demais, então começamos igualando as bases. Para “sumir” com a raiz, basta trocá-la pela potência correspondente, como indica as propriedades de potenciação!
Veja o exemplo:
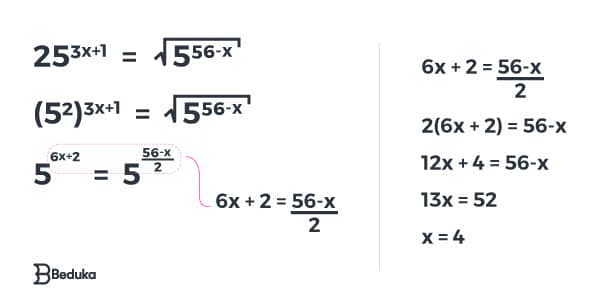
Equação exponencial com fração
Quando houver frações, basta pensar em qual potência aquele numerador pode ser trocado e o mesmo com o denominador. Depois, resolve-se normalmente. Caso a fração esteja na potência, aplica-se as propriedades de potenciação!
Veja os exemplos:
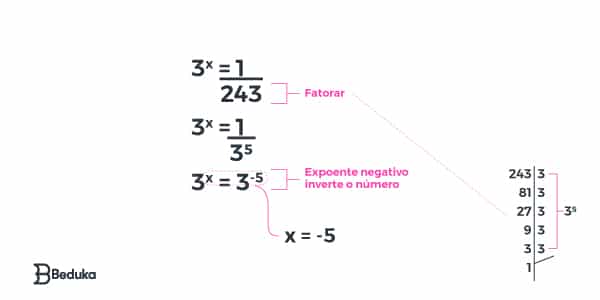
Equação exponencial com bases diferentes
Mas, e se as bases não forem iguais? Calma! Sempre tem um jeito! O primeiro recurso já foi dito: Fatoração! Se não resolver ou não for possível, podemos podemos aplicar os Logaritmos para auxiliar ou tentar o seguinte recurso:
Sempre que tiver o número 1 de algum lado, basta trocar pela base desejada e elevá-la a 0! Veja:
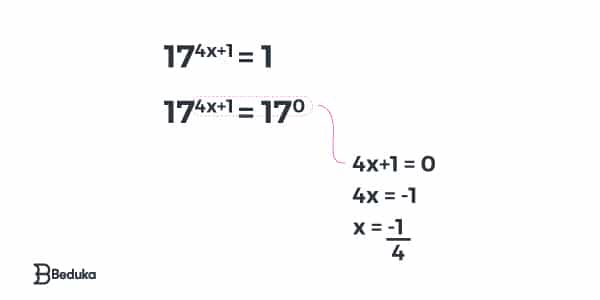
Gostou do nosso artigo sobre Equação Exponencial? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet, e o melhor: totalmente gratuito!
Queremos te ajudar a encontrar a FACULDADE IDEAL! Logo abaixo, faça uma pesquisa por curso e cidade que te mostraremos todas as faculdades que podem te atender. Informamos a nota de corte, valor de mensalidade, nota do MEC, avaliação dos alunos, modalidades de ensino e muito mais.
Experimente agora!





