Se você está procurando melhorar suas habilidades, veio ao lugar certo! Neste artigo, vamos te mostrar cinco ótimos exercícios de Geometria Plana para você expandir sua mente.
As questão que apresentaremos aqui são adequadas para alunos de diferentes níveis de habilidade em matemática. Eles são acessíveis, mas também desafiadoras o suficiente para aumentar suas habilidades em Geometria Plana.
Então, se você estiver pronto para se divertir enquanto aprende, vamos começar com um resumo para refrescar a memória e depois fazer os exercícios para desafiar seu cérebro!
Clique em um dos tópicos para ir direto ao conteúdo da sua escolha:
- O que é Geometria Plana?
- Quais são os principais conceitos da geometria plana?
- Lista de exercícios sobre Geometria Plana!
- Gabarito dos exercícios de Geometria Plana.
Esse assunto cai muito no Enem. E você está a poucos cliques de baixar o nosso Plano de Estudos para te guiar nesse jornada rumo à aprovação!
O que é Geometria Plana?
A Geometria Plana é a área da matemática que estuda as figuras de duas dimensões: altura e largura. É como uma folha do caderno, só possui superfície!
Estamos falando das formas que podem ser representadas no plano cartesiano. Provavelmente, você já ouviu falar delas: retângulos, quadrados, círculos, triângulos, etc.
É nessa matéria que estudamos os conceitos, posição e estrutura das formas. Também entendemos os conceitos básicos de ponto, reta, plano e ângulo. Por fim, aprendemos como calcular altura, área e perímetro.
Nós também temos um artigo explicando como aprender Geometria do Zero!
Quais são os principais conceitos da geometria plana?
Como a geometria plana estuda as figuras planas, precisamos começar com os conceitos básicos que formam essas figuras: ponto, reta e plano.
Vamos relembrar um pouquinho de cada um deles:
O que é um Ponto?
Os pontos não possuem uma definição, são adimensionais. Assim, não podemos medir sua altura, comprimento ou largura.
Como consequência, a nossa maneira de representá-lo visualmente é fazer, literalmente, um pontinho no papel.
O que é uma Reta?
Por definição, uma reta é formada por infinitos pontos seguidos. Ela tem uma dimensão, ou seja, é uma “linha” com comprimento.
Ela costuma ser representada por uma letra minúscula. As retas podem aparecer em 3 posições: horizontal, vertical ou inclinada.
Posição relativa entre retas
Quando estamos analisando diferentes retas ao mesmo tempo, dependendo da forma que elas se cruzam, podemos dar nomes a esses fenômenos:
- Retas paralelas: quando elas não possuem nenhum ponto em comum, estão perfeitamente alinhadas lado a lado. O símbolo usado para representar é: c // b , ou seja, a reta c é paralela a b.
- Retas concorrentes: quando as retas possuem um único ponto em comum, ou seja, se cruzam em um único lugar. Dependendo do ângulo que formam quando se cruzam, ainda podem ser classificadas em perpendiculares ou transversais.
- Retas coincidentes: são retas que estão sobrepostas, ou seja, possuem todos os pontos em comum. Nesse caso, elas são iguais.
O que é um Segmento de Reta?
O segmento de reta é definido como uma parte da reta. Isso significa que pegamos uma parte da reta (infinita) e delimitamos um segmento (finito). Por isso, o segmento de reta tem início e fim.
O que é uma Semirreta?
O conceito de semirreta surge quando queremos pegar um único ponto da reta como extremidade, mas analisamos tudo o que vem depois. Portanto, uma ponta é delimitada e a outra é infinita!
O que é um Plano?
Um plano é uma região que abrange infinitos pontos e infinitas retas. Ele possui duas dimensões, ou seja, tem comprimento e largura. Geralmente a região que o plano ocupa é representada por letras gregas
O que são Ângulos?
Você acabou de conhecer semirretas, retas e segmentos de reta, e também viu que elas podem se cruzar. Quando isso acontece, é possível determinar a inclinação que as retas formam entre si.
Essa região, que está entre duas semirretas, é chamada de ângulo. Ele é medido em graus e, por definição, essa medida vai de 0° a 360°.
Como os ângulos podem ser classificados?
- Agudo: se sua medida for menor que 90º;
- Reto: se sua medida for igual a 90º;
- Obtuso: se sua medida for maior que 90º e menor que 180º;
- Raso: se sua medida for igual a 180º.
O que é uma figura plana? (Polígonos)
Uma figura plana é uma região fechada formada por segmentos de reta. É preciso no mínimo 3 segmentos para que se forme uma região fechada (triângulo). A medida que os lados aumentam, temos outros nomes: quadriláteros, pentágonos, hexágonos…
Quando já temos uma figura formada, deixamos de falar “segmentos de reta” e chamamos simplesmente de lados.
Assim, seus elementos básicos são:
- Lado: os segmentos de reta que contornam e fecham a figura.
- Vértice: pontos de encontro que ligam os lados.
- Ângulos: áreas de inclinação entre os lados, ao lado dos vértices.
Tudo isso faz parte de um dos assuntos que mais caem no Enem, mas nós já fizemos uma lista te contando quais são os outros!
Exercícios sobre Geometria Plana
Esperamos que, com esse resumo, tudo tenha ficado mais claro para você.
Agora vamos ao que interessa:
1° dos exercícios sobre geometria plana – (UFMT)
Assinale a medida do lado de um quadrado, sabendo-se que o número que representa o seu perímetro é o mesmo que representa sua área.
a) 5.
b) 4.
c) 6.
d) 8.
2° dos exercícios de geometria plana – (ENEM)
Em canteiros de obras de construção civil, é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo conforme pode ser visto na figura, em que as estacas foram indicadas por letras.
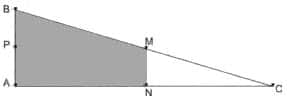
A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto. Nessas condições, a área a ser calçada corresponde
a) à mesma área do triângulo AMC.
b) à mesma área do triângulo BNC.
c) à metade da área formada pelo triângulo ABC.
d) ao dobro da área do triângulo MNC.
e) ao triplo da área do triângulo MNC.
3° dos exercícios sobre geometria plana – (ENEM)
A ideia de usar rolos circulares para deslocar objetos pesados provavelmente surgiu com os antigos egípcios ao construírem as pirâmides.
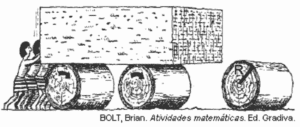
Representando por R o raio da base dos rolos cilíndricos, em metros, a expressão do deslocamento horizontal y do bloco de pedra em função de R, após o rolo ter dado uma volta completa sem deslizar, é:
a) y = R.
b) y = 2R.
c) y = πR.
d) y = 2πR.
e) y = 4πR.
- Ufa, estamos quase lá! Faça os dois últimos exercícios sobre Geometria Plana!
4° dos exercícios de geometria plana – (ENEM)
A rampa de um hospital tem na sua parte mais elevada uma altura de 2,2 metros. Um paciente ao caminhar sobre a rampa percebe que se deslocou 3,2 metros e alcançou uma altura de 0,8 metro. A distância em metros que o paciente ainda deve caminhar para atingir o ponto mais alto da rampa é
a) 1,16 metros.
b) 3,0 metros.
c) 5,4 metros.
d) 5,6 metros.
e) 7,04 metros.
5° dos exercícios sobre geometria plana – (ENEM)
Quatro estações distribuidoras de energia A, B, C e D estão dispostas como vértices de um quadrado de 40km de lado. Deseja-se construir uma estação central que seja ao mesmo tempo equidistante das estações A e B e da estrada (reta) que liga as estações C e D. A nova estação deve ser localizada
a) no centro do quadrado.
b) na perpendicular à estrada que liga C e D passando por seu ponto médio, a 15km dessa estrada.
c) na perpendicular à estrada que liga C e D passando por seu ponto médio, a 25km dessa estrada.
d) no vértice de um triângulo equilátero de base AB, oposto a essa base.
e) no ponto médio da estrada que liga as estações A e B.
- Parabéns, você fez todas as questões de Geometria Plana! O gabarito está logo adiante.
Avance de nível e treine com o nosso Simulado Enem logo depois de ver as respostas!
Respostas dos Exercícios de Geometria Plana
Exercício resolvido da questão 1 –
Alternativa Correta: b) 4.
Exercício resolvido da questão 2 –
Alternativa Correta: e) ao triplo da área do triângulo MNC.
Exercício resolvido da questão 3 –
Alternativa Correta: e) y = 4πR.
Exercício resolvido da questão 4 –
Alternativa Correta: d) 5,6 metros.
Exercício resolvido da questão 5 –
Alternativa Correta: c) na perpendicular à estrada que liga C e D passando por seu ponto médio, a 25km dessa estrada.
Gostou dos nossos exercícios de Geometria Plana? Compartilhe com os seus amigos e comente abaixo sobre algo que você deseja mais explicações. Ah, nós também temos exercícios de Geometria Espacial e de Geometria Analítica!
Nós também queremos te conectar à faculdade! Experimente fazer o Teste vocacional ou procurar uma vaga no seu curso dos sonhos com desconto no Beduka Bolsas. Por lá você pode encontrar o que está procurando e não vai se arrepender de ter se dado uma chance.
Boa sorte!






12 Comentários
Os conceitos de “retas concorrentes” e “retas paralelas” estão trocados.
Você é um bom aluno, Luis! Obrigado por avisar, já está atualizado. 🙂
Iria ser muito interessante se as questões fossem comentadas.
Essa é uma atualização que ainda faremos, Joan! Obrigado pela dica. 🙂
Olá. As resposta poderiam vir com as explicações de como chegar nela. Obg
Estamos trabalhando para fazer essa atualização em nosso conteúdo Renan.
Por que a resposta do exercício 3 é E (4 PI R) e não é D (2 PI R)? Uma volta do cilindro não é o perímetro do círculo?
Olá, Rogério. Acontece que o ponto mais alto existente no cilindro, tem a velocidade igual ao dobro da velocidade do centro. Quando o tambor dá uma volta completa, o centro deste mesmo tambor desloca-se 2πR e o objeto que está em contato com o ponto mais alto desloca-se o dobro, ou seja, 4πR.
Olá amigos do Beduka, apesar da explicação acima, ainda acho que a resposta correta é 2πR. Gostaria de ter uma demonstração. Se o rolo não desliza, o ponto inicialmente em contato com ele só pode ter se deslocado 2πR depois de uma volta completa.
Vanir, essa questão gerou bastante polêmica à época. Mas veja que a pergunta é sobre o deslocamento do bloco. O quanto ele está mais para a frente? Neste caso, é a letra E que responde, pois o bloco vai para o rolo seguinte, somando duas voltas de circunferência.
Por que na questão, a resposta é a letra C?
Silvio, se fizermos um desenho usando as instruções no enunciado da questão e usarmos Pitágoras teremos: BG2 = BN2 + NG2. Isso dá X2 = (20)2 + (40 – x)2. Resolvendo a equação chegamos à resposta da letra C.