O triângulo equilátero é um dos tipos mais comuns de triângulo que existem, por isso aparece tanto nas provas! Ainda assim, muitos estudantes travam na hora de saber como calcular a altura de um triângulo equilátero… Por isso, nós vamos te mostrar 4 formas de fazer isso.
Neste artigo, você irá entender cada método e pode memorizar aquele que tiver mais afinidade. Até porque, as questões vão te dar dados diferentes e aí você terá que jogar naquele jeito que melhor se encaixar.
Pode parecer muita coisa, mas fizemos uma explicação cheia de exemplos e com linguagem simples para você aprender do zero. Vamos lá desvendar esse mistério?
Neste artigo explicando como achar a altura de um triângulo equilátero, você encontrará todos os temas abaixo. Clique em um deles para ir diretamente ao conteúdo:
- Introdução ao triângulo equilátero: características úteis!
- Primeiro jeito: um caminho simples e fácil usando Teorema de Pitágoras
- Segundo jeito: como calcular a altura de um triângulo equilátero usando a fórmula
- Terceiro jeito: como calcular a altura de um triângulo qualquer?
- Quarto jeito: a trigonometria básica ajuda a calcular a altura do triângulo retângulo.
Antes de continuar, saiba que essa matéria é essencial para o Enem e nós temos um Plano de Estudos para te guiar nessa jornada!
Introdução ao triângulo equilátero: características úteis
O triângulo equilátero é o queridinho dos estudantes de Geometria Plana, pois é o mais fácil de todos!
Isso porque ele tem muitas características iguais que se repetem, então entrega o raciocínio e facilita nossa vida. Mas só quem realmente entende suas propriedades é que consegue interpretar.
Por isso, vamos relembrar suas 3 características essenciais a seguir!
Lados iguais
A própria palavra equilátero já nos conta sobre essa propriedade: “equi = igual” e “látero = lado”
Dessa forma, se for dado a medida de um dos lados, sabemos que todos os demais são iguais.
Você sabia que no triângulo isósceles somente dois lados são iguais e o terceiro é sempre diferente?
Ângulos iguais
Não importa o tamanho do triângulo equilátero, se você usar um transferidor (medidor de ângulos), sempre encontrará o mesmo valor para todos os seus ângulos!
Isso acontece por um motivo: para que todos os lados iguais se encontrem em um formato perfeito, os ângulos precisam estar igualmente divididos também.
E isso nos leva a afirmar uma coisa: se em qualquer triângulo a soma dos ângulos internos é 180°, e no triângulo equilátero todos os ângulos são iguais, então podemos fazer 180°/3 = 60°.
Logo, todos os ângulos de um triângulo equilátero sempre medirão 60°.
E assim chegamos a um novo conceito: ele é equiângulo.
Nós também temos um artigo explicando tudo sobre ângulos!
Alturas iguais
Adivinhe só, se tudo nesse triângulo é igual, agora não seria diferente.
Não importa a partir de qual lado você trace a altura, elas sempre serão iguais!
Lembre-se: altura é um segmento de reta que forma um ângulo reto (90°) com a superfície.
1° O caminho mais seguro: Teorema de Pitágoras
Agora que já relembramos o básico, já podemos começar a falar sobre como descobrir a altura do triângulo equilátero.
E o primeiro método é usando o Teorema de Pitágoras.
Vamos fazer uma breve explicação sobre ele e já partir para o exemplo!
O que é o Teorema de Pitágoras?
Na matemática, teorema é uma fórmula que sempre é aplicada em uma situação específica. No caso do Pitágoras, ele deve ser usado somente em triângulos retângulos (um dos ângulos mede 90°).
Você deve estar pensando então como usaremos isso no triângulo equilátero… A resposta está na imagem logo adiante!
Antes, vamos só relembrar a fórmula desse teorema:
cat² + cat² = hip²
- A hipotenusa (hip) é o lado oposto ao ângulo reto, ou seja, é o maior lado de um triângulo retângulo.
- Os catetos (cat) são os lados restantes, ou seja, os lados adjacente ao ângulo reto.
Como calcular a altura de um triângulo equilátero usando Pitágoras? 3 passos!
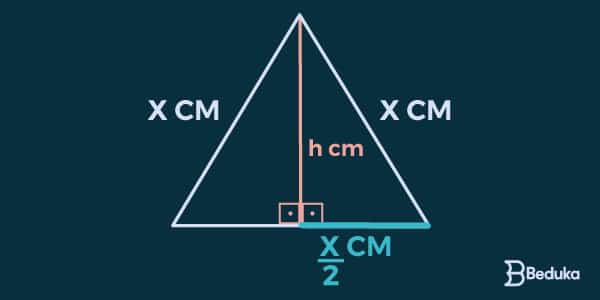
- 1° Passo: devemos traçar a altura do triângulo equilátero. Lembrando que ela parte do vértice superior e vai até o meio da base do lado oposto, coincidindo com a mediana.
- 2° Passo: observe que formamos dois triângulos retângulos iguais dentro do equilátero. É para isso que traçamos a altura, já que ela sempre forma 90° com a superfície.
- 3° Passo: Agora, podemos usar o teorema: cat² + cat² = hip². Basta substituir cada informação no seu lugar!
Lembre-se: nessa fórmula, a altura (h) ocupa o lugar de um dos catetos (cat).
2° A fórmula da altura do triângulo equilátero
Talvez você já tenha aprendido e esquecido… Mas existe uma fórmula específica para calcular a altura de um triângulo equilátero, e só funciona nessa figura.
Pode parecer coincidência, mas ela foi tirada do Teorema de Pitágoras. Assim, se você souber o primeiro jeito, não esquecerá este segundo!
Deduzir uma fórmula é entender qual o raciocínio usado para chegar nela… E a história dessa fórmula é a seguinte: um matemático já sabia usar Pitágoras para calcular a altura, mas ele só usava números.
Aí ele resolveu substituir os números pelas letras que representam as partes do triângulo equilátero. E chegou a uma fórmula geral:
h = x √3 / 2.
Atenção: Ela nos ajuda a achar o valor da altura (h) se tivermos o lado (x). Basta substituir os valores dados na questão e teremos a resposta!
Exemplo com números e solução:
- 1) Calcule a altura de um triângulo equilátero de lado 4cm.
Solução 1: se tiver decorado a fórmula geral, basta colocar o 4 no lugar do x:
h = x√3 / 2
h = 4√3 / 2
h = 2√3
Solução 2: se esqueceu da fórmula, pode usar o Pitágoras mesmo:
cat² + cat² = hip²
h² + (4/2)² = 4²
h² + 4 = 16
h² = 12
h = √12 (simplificando = 2√3)
Você está a poucos cliques de treinar para o Enem com o nosso Simulado online e gratuito!
3° Como calcular a altura de um triângulo qualquer?
Ok, já te mostramos dois jeitos bem direcionados para o triângulo retângulo. Mas também existe uma jeito de calcular alturas de triângulos aleatórios, independente do tipo. Para saber como encontrar a altura de um triângulo qualquer, é possível usar a fórmula da área.
Nós falamos assim: “área é igual à base vezes a altura dividido por 2 “.
Que pode ser escrito como:
A = (b.h)/2
Sendo que:
- A = área do triângulo.
- b = comprimento da base do triângulo (a base é onde a altura se encontra e forma 90º).
- h = Altura do triângulo (Sai de um vértice e forma 90º com a base).
Se você tiver os valores da base e da área, basta substituir na fórmula para encontrar a altura!
“E como eu acho a área e a base?”
A base é muito simples: ela é a medida de qualquer um dos lados, porque nesse triângulo tudo é igual! Mas, por definição, base é o lado que recebe o ângulo formado quando traçamos a altura.
Agora olha que coisa louca: para encontrar a área nós precisamos da altura. Mas a altura é justamente o que já estávamos procurando nessa situação!
Então não tem jeito… você só consegue usar a fórmula da área para encontrar a altura se o valor da área e do lado forem dados. Se não, você terá que encontrar a altura usando o Pitágoras ou a fórmula específica que ensinamos aí para trás!
Nós estamos estudando esse assunto da geometria plana, mas alguns desses conceitos podem aparecer também na geometria espacial e na analítica.
4° Para os curiosos: trigonometria básica no triângulo equilátero e sua altura
Nós sabemos, muita gente tem birra da trigonometria. Mas não precisa ser assim, ela é mais legal do que aparenta! Além do mais, nós vamos trabalhar só com a parte básica.
A trigonometria é uma ferramenta da matemática que leva em conta os ângulos e os lados que formam ele.
Você lembra das relações de semelhança nos triângulos? A ideia que a trigonometria traz é parecida: sempre que pegarmos dois valores específicos e dividimos eles, nos dará um mesmo resultado.
Assim, podemos estabelecer três relações trigonométricas:
- Seno: é um valor específico para cada ângulo, quando pegamos o cateto (lado) oposto a ele e dividimos pela hipotenusa.
- Cosseno: é um valor específico para cada ângulo, quando pegamos o lado que encosta nele (adjacente) e dividimos pela hipotenusa.
- Tangente: é um valor específico para cada ângulo, quando pegamos o cateto oposto e dividimos pelo adjacente.
Viu? Tudo tranquilo. Agora vamos ver como podemos usar isso para achar a altura:
Como calcular a altura de um triângulo equilátero usando trigonometria?
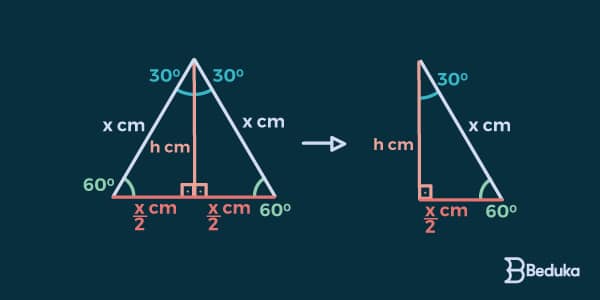
Você lembra que em todo triângulo equilátero todos os ângulos medem 60°. Então podemos fazer assim:
- 1° Passo: novamente devemos traçar a altura no t. equilátero. Aí teremos dois t. retângulos.
- 2° Passo: logo percebemos que, por se tratar de um triângulo equilátero, a altura será também a bissetriz (divide o ângulo em duas partes iguais). Também será a mediana da base (divide o lado em 2 partes iguais).
- 3° Passo: ai ficou fácil. Se for dado o valor do lado desse triângulo, podemos aplicar as relações da trigonometria!
Teremos então o 60° e o 30°. Eles são conhecidos como ângulos notáveis. Agora só precisamos lembrar desses valores e substituir na relação trigonométrica.
Atenção!
- Se escolhermos o ângulo de 30°, a altura é o cateto adjacente (usaremos cosseno).
- Se escolhermos o ângulo de 60°, a altura é o cateto oposto (usaremos seno).
- Observe que X (o lado do triângulo) sempre será a hipotenusa.
Vamos escolher o 60° como referência. Ficará assim:
sen 60° = cat. oposto / hipotenusa
sen 60° = h / x
√3/2 = h / x
x√3 / 2 = h
Opa! Você já viu esse resultado antes… é exatamente igual à fórmula específica para calcular a altura do triângulo retângulo.
Tudo na matemática faz sentido e está relacionado!
Acabou! Vamos resumir:
Para finalizar, vamos só recapitular: em uma questão sobre como calcular a altura de um triângulo equilátero, você pode optar por 4 caminhos:
- Usar Teorema de Pitágoras.
- Usar trigonometria.
- Decorar a fórmula específica e substituir o valor dado.
- Usar a fórmula da área.
Gostou do nosso artigo ensinando como calcular a altura de um triângulo equilátero? Compartilhe com os seus amigos e comente abaixo sobre algo que você deseja mais explicações.
Nós também queremos te conectar à faculdade! Experimente fazer o Teste vocacional ou procurar uma vaga no seu curso dos sonhos com desconto no Beduka Bolsas. Por lá você pode encontrar o que está procurando e não vai se arrepender de ter se dado uma chance.
Boa sorte!






12 Comentários
Pessoal, a dedução da fórmula da altura está errada. Ao elevarmos (x/2) ao quadrado, temos (x/2)² = x²/4 e não x²/2, como foi feito na imagem. Após isso, teremos:
x² = h² + x²/4
h² = x² – x²/4
h² = 4x²/4 – x²/4
h² = 3x²/4
h = x√3/2
Livia, o processo que você fez foi o mesmo do nosso. Apensa representamos de uma forma gráfica diferente. Nossa imagem não representa (x/2) ao quadrado. Ela representa somente X ao quadrado dividido por 2.
Jogo dos 7 erros. Além do outro erro já comentado, tem também o erro de passar pro outro lado somando ao invés de diminuindo, e no final não foi tirada a raiz do 2 no denominador.
Boa tarde Cláudio, foi um erro de design mesmo. Já consertamos. Obrigada por avisar!
O processo para encontrar a altura do triângulo equilátero está errado, pois o denominador não foi elevado ao quadrado e ao trocar de membro não houve inversão de operação, embora, com esses dois erros, chegou na fórmula da altura.
Sim Thaise, bem notado. Já atualizamos a imagem, foi um erro de design mesmo. Obrigada!
Por que h^2 ficou 4h^2?
Oi Deiv, você está se referindo a qual parte do texto?
Vou supor que é sobre a terceira linha da imagem dedução da fórmula.
Nesse caso, é porque fizemos o MMC.
Note que na segunda linha precisávamos somar dois números com denominadores diferentes (o h² sobre 1 e o x² sobre 4).
Realizando a operação de soma de frações, tiramos o MMC dos denominadores, dividimos-o pelo denominador original e multiplicamos pelo numerador.
Vou deixar a sugestão (malandra) da quinta fórmula para calcular a altura de um triângulo equilátero: lado do triângulo x 0,866. ……kkkkkk
kkkkkk essa foi boa.
no triangulo equilatero e fazer 5 mais 2 a dividir por 2 e da 123 mais o perimetro fa figura que 5
Não entendemos muito bem seu comentário, Rodolfo. Pode explicar melhor?