Geometria Analítica: fórmulas e explicações com exemplos!

Apesar de intimidar alguns, com explicações simples você é capaz de aprender Geometria Analítica! Ela é a área que representa as figuras planas por meio de equações, então aprendemos a calcular distância entre pontos, circunferências e retas. Conheça as fórmulas e veja os exemplos!

Neste artigo sobre Geometria Analítica, você encontrará:

1. O que a Geometria Analítica estuda?
2. Como e quando ela surgiu?
3. Onde ela é usada?
4. O que eu preciso saber para aprendê-la?
5. Estudo dos pontos: distância entre dois pontos, ponto médio, condição de alinhamento.
6. Estudo da reta: equação geral e reduzida, casos de interseção e distância entre ponto e reta.
7. Estudo da circunferência: equação reduzida, ponto e circunferência, reta e circunferência, relação entre duas circunferências.

• Estudando para as provas? Conheça O melhor Simulado do Brasil! Ele pode ser personalizado com as matérias que você mais precisa!

O que estuda a geometria analítica?

A Geometria analítica é a área da matemática que estuda as figuras da geometria plana usando expressões algébricas.

Isso significa que as relações entre ponto, reta e circunferência podem ser dadas por equações e pares de coordenadas no plano cartesiano!

Por isso mesmo, ela também pode ser chamada de geometria de coordenadas ou geometria cartesiana.

Como e quando surgiu a geometria analítica?

A Geometria Analítica surgiu com René Descartes em 1637, o mesmo matemático e filósofo que criou o sistema de coordenadas no plano cartesiano. O seu lema de vida era que o pensamento matemático poderia trazer o conhecimento de qualquer área.

No século XVII, Descartes relacionou a álgebra com a geometria, traduzindo a linguagem das formas para a das contas! Assim, criou princípios matemáticos que foram a conclusão de seu trabalho.

Onde é utilizada a geometria analítica?

A geometria analítica é muito utilizada na física e na engenharia, ou seja, é utilizada na computação, nos assuntos espaciais, nas construções civis e mecânicas.

Essa matemática é muito importante na vida de um estudante do Ensino Médio e de um vestibulando. Isso porque é uma matéria que cai nas provas de matemática e nos ajuda a compreender a física que trata dos vetores.

Os grandes cientistas Isaac Newton e Gottfried Wilhelm Leibniz foram estudantes assíduos da Geometria Analítica! Ela deu a base teórica e prática para o surgimento do Cálculo Diferencial e Integral, muito utilizado atualmente na Engenharia.

O que eu preciso saber para aprender geometria analítica?

Antes de estudarmos os conceitos da Geometria analítica, é preciso já saber os conceitos da geometria plana. Os principais são a definição de ponto, reta, plano, triângulos, quadriláteros e circunferências.

Além disso, vamos utilizar conceitos que se aplicam a várias áreas da matemática. O significado de “paralelo” (perfeitamente alinhados, não se cruza), “perpendicular” (forma ângulo reto), “congruente” (mesmo valor), são exemplos!

Por fim, é essencial conhecer a equação do primeiro grau e os elementos que compõem o plano cartesiano e sistema de coordenadas.

• Portanto, leia esses artigos antes de continuar! Aproveite para seguir o Beduka no Instagram para conteúdos diários.

Conceitos importantes da geometria analítica

Listamos abaixo os tópicos que veremos na geometria analítica, para você ter noção do que trataremos. Nos próximos tópicos, explicaremos cada conceito separadamente, com imagens e fórmulas!

Estudo dos Pontos

• Distância entre dois pontos;
• Ponto médio de um segmento;
• Condição de alinhamento de três pontos.

Estudo da Reta

• Equação geral e reduzida da reta;
• Intersecção entre retas;
• Distância entre ponto e reta.

Estudo da Circunferência

• Equação reduzida da circunferência;
• Posições relativas entre ponto e circunferência;
• Posições relativas entre reta e circunferência;
• Posições relativas entre circunferências.

Estudo dos pontos

Segundo a geometria plana, o ponto é definido como algo que “não tem partes”. 

Ele possui apenas uma dimensão, ou seja, é literalmente um pontinho! Exatamente como o ponto final ou quando você faz um ponto com a caneta sobre uma folha!

Ele é usado apenas como uma referência de posição no espaço e é representado por letras maiúsculas.

Agora, vamos ver como isso se relaciona com a álgebra:

Distância entre dois pontos

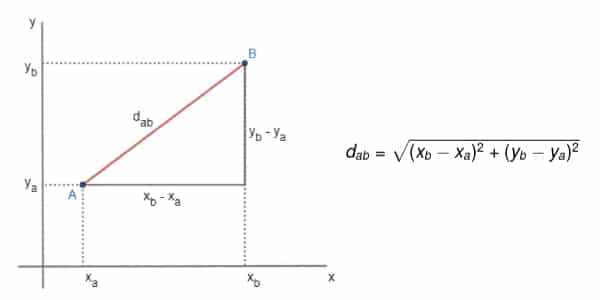
Na geometria analítica, nós aprendemos como calcular a distância entre os pontos. 

Se tivermos como base os pontos A (xa, ya) e B (xb, yb), a distância é representada pelo segmento de reta AB (dAB). 

Note que a distância entre os pontos A e B é a hipotenusa do triângulo. Portanto, vamos utilizar o teorema de Pitágoras para definir uma fórmula genérica. 

Tudo isso foi representado na imagem acima!

Observe que fizemos “xb – xa” para achar a medida do cateto (lado) do triângulo que é paralelo ao eixo x. O mesmo foi feito com a operação “yb – yb” para achar a medida do cateto paralelo ao eixo y. 

Com essas medidas podemos aplicar o teorema e encontrar a hipotenusa!

• Exemplo

Calcule a distância entre os pontos A (0, 0) e B (4, 2).

Resolução:

Coordenadas do ponto médio

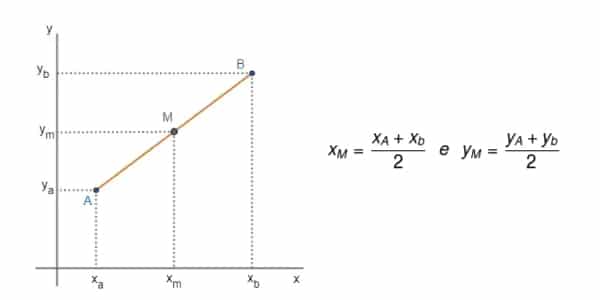
Na geometria plana, o conceito de ponto médio (M) é aquele que divide um segmento ao meio exato, ou seja, em duas partes iguais. 

Na geometria analítica, podemos calcular as coordenadas do ponto médio com a fórmula na imagem acima!

• Exemplo

Determine o ponto médio do segmento AB, sabendo que A (2, 1) e B (6, 5).

Resolução:

Condição de alinhamento de três pontos

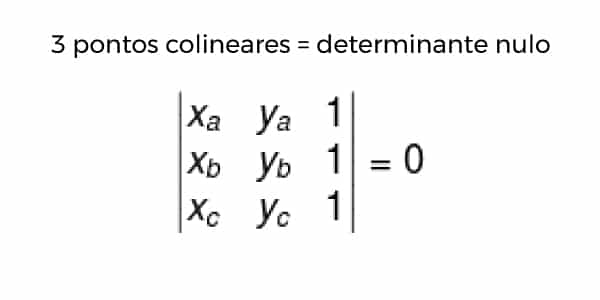
Imagine que você precise saber se três pontos estão alinhados (na mesma reta) ou não, sem ter um desenho do plano para ver…

Pois é, é possível saber com certeza por meio da álgebra desde que tenhamos seus pares de coordenadas!

Considere três pontos genéricos: A (xa, ya), B (xb, yb) e C (xc, yc). Dizemos que os pontos são colineares se o determinante entre eles for nulo (igual a zero). 

Lembre-se: determinante é uma função que vem da matriz, sempre sinalizada pelos dois traços ao lado dela! Ele transforma aquela matriz, resumindo suas informações em um único número final!

Estudo da Reta

Segundo a geometria plana, a reta é formada por infinitos pontos seguidos. Ela tem uma dimensão, ou seja, é uma “linha” com comprimento e sem largura. 

Ela costuma ser representada por uma letra minúscula. 

É importante definir que é preciso no mínimo dois pontos para traçar uma reta. Assim, a reta é infinita, não tem começo ou fim, embora nós só representemos uma parte.

Dizemos que há apenas uma reta que passa por dois pontos específicos. Mas, por um ponto qualquer e sozinho, podem passar infinitas retas porque são várias as possibilidades de ele se agrupar com outro ponto!

Agora, vamos ver como isso se relaciona com a álgebra:

Equação geral da reta

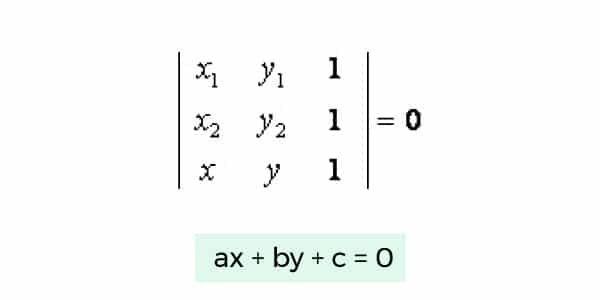
A equação geral das retas é definida genericamente por:

 ax + by + c = 0

Isso significa que todas as equações das retas seguem esse molde, só mudam os números que irão diferenciar a posição dessas retas.

Nesta fórmula, os números dos pontos que a compõem são colocados no lugar de “x” e “y”, referindo as coordenadas. “a”, “b” e “c” são coeficientes que determinam outras características, como inclinação.

Na realidade, nós temos o costume de usar mais a fórmula reduzida (aprenderemos em seguida). Então, o importante aqui é você saber como achar a equação geral de uma reta a partir de pares ordenados!

Para determinarmos a equação geral de uma reta, precisamos aplicar a regra de Sarrus no determinante dos pontos que estarão alinhados para formar a reta. 

Ela também envolve matrizes e determinantes, e precisamos de no mínimo dois pares ordenados que pertençam à reta!

Na matriz, colocamos os pares ordenados que devem ser informados: (x1, y1) e (x2, y2) e um ponto genérico representado por (x, y). Esse último é o que compõe a fórmula genérica.

Observe que a 3º coluna da matriz é completada com o algarismo 1, pois só conseguimos fazer contas com uma matriz quadrada, ou seja, simétrica (3×3). 

Assim, completando a coluna faltante com o número 1, não alteraremos o resultado e teremos como prosseguir calculando o determinante!

A regra de Sarrus nos indica

• 1º passo: repetir a 1º e a 2º coluna da matriz.
• 2º passo: somar os produtos dos termos da diagonal principal.
• 3º passo: somar os produtos dos termos da diagonal secundária.
• 4º passo: subtrair a soma total dos termos da diagonal principal dos termos da diagonal secundária.

• Exemplo

Encontre a equação geral da reta que passa pelos pontos A(1, 2) e B(3,8):

Ponto A: x1 = 1 e y1 = 2

Ponto B: x2 = 3 e y2 = 8

Ponto genérico C (x, y)

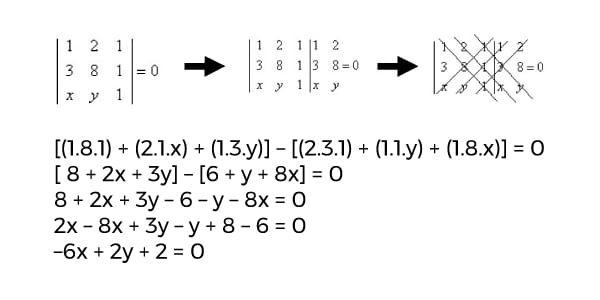
Portanto, os pontos A(1, 2) e B(3,8) pertencem a seguinte equação geral da reta: –6x + 2y + 2 = 0.

Equação reduzida da reta

A equação reduzida da reta é dada por:

y = mx + n

A essa altura, você deve ter notado a influência dessa fórmula na composição da nossa famosa “f(x) = ax + b”, não é?

Realmente, a função de primeira grau possui um gráfico cujo desenho é uma reta! Então, leia esse artigo antes de continuar, porque usaremos alguns conceitos adiante (m é o coeficiente angular e n é o coeficiente linear)!

Para encontrar a equação reduzida de uma reta, é necessário descobrir os valores do coeficientes e montar a equação final! 

Há ainda a possibilidade de encontrar o valor do coeficiente angular e conhecer um ponto. Só é preciso duas informações para encontrar o resto!

O coeficiente linear (n ou b) é simples: basta saber que ele é o valor da ordenada (y) quando x = 0. Isso significa que n é onde a reta corta o eixo y, o ponto (0,n).

Para calcular o coeficiente angular (m ou a)da reta, existem duas possibilidades: 

• Saber que ele é igual à tangente do ângulo α:

m = tg α 

• Usar a fórmula quando se tem dois pontos coordenados da reta:

Seja A(x1,y1) e B (x2,y2), então o coeficiente angular pode ser calculado por:

m = y2 – y1 / x2 = x1

Para tomar a decisão sobre qual método utilizar para calcular o coeficiente angular da reta, primeiro é necessário analisar quais são as informações que temos.

Intersecção entre retas

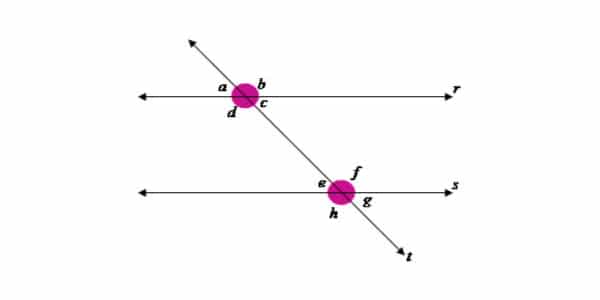
Chegamos à uma parte mais teórica da matéria, sem fórmulas! 

Imagine que temos retas que se interceptam de forma transversal ou perpendicular.

É importante notar que todos os ângulos formados por um cruzamento perpendicular são de 90°. 

Contudo, no caso de retas paralelas e transversais, temos diferentes ângulos como esquematizado na imagem acima!

Observe que as retas r e s são paralelas (r//s), não possuem ponto em comum. A reta t é transversal às retas r e s, formando quatro ângulos com a reta s e quatro ângulos com a reta t.

Esses 8 ângulos recebem nomes de acordo com a posição:

• Ângulos correspondentes: a, b, c, d, e, f, g, h. 

Isso significa que cada um tem um par congruente (mesmo valor), porque ocupa uma mesma posição relativa, análoga: a = e, b = f, c = g, d = h

• Ângulos colaterais externos: a, b, h, g. 

Isso significa que estão do mesmo lado em relação a reta t e externos às retas paralelas (mais distantes, nas extremidades). Eles acabam sendo suplementares: a + h = 180º e b + g = 180º

• Ângulos alternos externos: a, b, g, h.

Isso significa que estão em lados opostos da reta t, mas externos em relação às retas paralelas: a e g, b e h.

• Ângulos alternos internos: c, e,d,f.

Significa que estão em lados opostos mas na região de dentro formado entre as retas paralelas:c e e , d e f. Eles também são congruentes!

• Ângulos colaterais internos: c,f,d,e.

São aqueles que estão no mesmo lado em relação à reta t e na área interna das retas paralelas: c e f, d e e. Eles são suplementares!

Distância entre ponto e reta

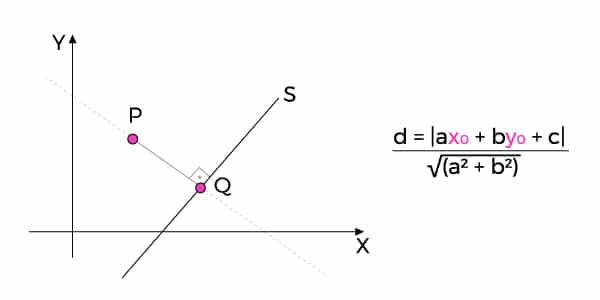
Pode acontecer de você se deparar com um ponto aleatório no meio do plano, que não passa por sua reta. 

Neste caso você precisará calcular a distância entre esses elementos. A distância entre um ponto e uma reta é representada por um segmento que une eles, formando um ângulo reto (90°) no encontro. 

Antes de iniciar os cálculos, precisamos ter a equação geral da reta (ax + by + c = 0) e a coordenada do ponto (x0,y0). É por meio desses dois elementos que os matemáticos criaram a fórmula que nos dará a distância:

• Exemplo

Dado o ponto A(3, -6), estabeleça a distância entre o ponto e a reta r: 4x + 6y + 2 = 0.

Resolução:

Estudo da Circunferência

Segundo a geometria plana, a circunferência é uma linha (não reta) formada por todos os pontos que estão a uma mesma distância de um ponto central. Essa distância é chamada de raio (r).

Então, a circunferência (C) é o contorno que delimita o círculo e o círculo é a região que fica limitada pela circunferência.

Agora, vamos ver como isso se relaciona com a álgebra:

Equação reduzida da circunferência

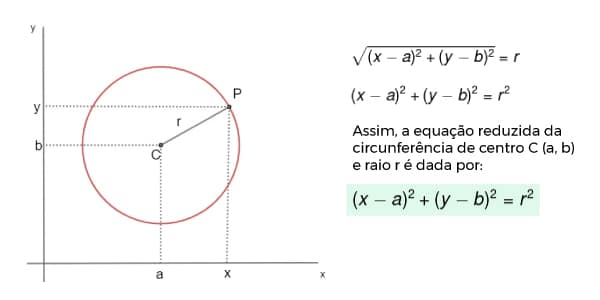
Assim como para as reta, é possível determinar a equação de uma circunferência. Para isso, é necessário conhecer as coordenadas do seu centro e a medida do seu raio!

Essa equação é tão importante que tem muita aplicação no nosso dia a dia. Exemplo disso é o funcionamento dos radares aéreos, marinhos e terrestres!

Na realidade, existe mais de uma forma algébrica de representarmos uma circunferência. Mas, a que você precisa saber é a equação reduzida indicada na imagem acima.

Para conferirmos se realmente se trata de uma circunferência, é preciso que a distância entre o centro e um ponto qualquer da superfície seja exatamente o valor do raio. Ou seja:

dPC = r

Assim, basta pegar a fórmula da distância entre dois pontos e igualar com o raio. Desenvolvendo o cálculo, chegamos a fórmula reduzida da circunferência apresentada na imagem acima!

Atenção: Note que se nos for dada uma fórmula nesse estilo, já batemos o olho e identificamos a posição do centro e até o valor do raio. 

Basta notar que os sinais anteriores aos pontos são negativos, portanto o ponto será o inverso. O valor que representa o raio está elevado ao quadrado, portanto basta tirar a raiz do número.

• Exemplo:

A equação (x – 3)2 + (y – 4)2 = 169 representa uma circunferência de centro C (3, 4) e raio r2 = 169, ou seja, r = 13.

A equação x2 + y2 = 4 representa uma circunferência centrada na origem do sistema (0,0) e raio 2.

Posições relativas entre ponto e circunferência

Quando comparamos as posições que um ponto tem em relação ao raio, podemos ter 3 diferentes fenômenos acontecendo. Veja:

• Ponto interno à circunferência: a distância do ponto P até o centro é menor do que o raio da circunferência. 

• Ponto externo à circunferência: a distância do ponto P até o centro é maior do que o raio.

• Ponto pertence à circunferência: a distância do ponto P ao centro é igual ao raio.

Para identificarmos se a distância do ponto é maior ou menor que raio, precisamos usar a fórmula da distância entre dois pontos, vista nos tópicos anteriores.

• Exemplo:

Analise as posições relativas entre os pontos A(-2,2). B (-4,1), D(1,1), E(-4,-1) e a circunferência c: (x+1)2 + (y+1)2 = 9.

Resolução:

Posições relativas entre reta e circunferência

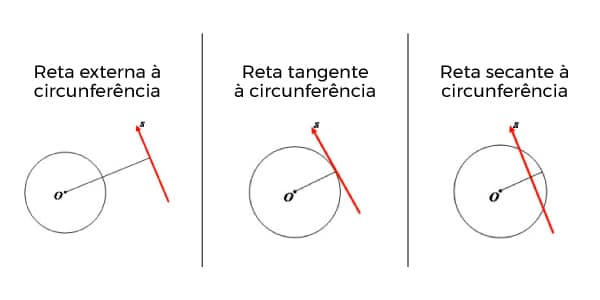
Quando comparamos uma reta com a circunferência, também há 3 possíveis posições que recebem nomes específicos dependendo da intersecção que há entre elas:

• Reta externa à circunferência: é aquela reta que não possui nenhum ponto em comum com a circunferência. Assim, a distância do centro da circunferência até o ponto mais próximo da reta s é maior que o raio da circunferência: D > r.

• Reta tangente à circunferência: é aquela que possui 1 único ponto de intersecção. Assim, a distância do centro O até o ponto mais próximo da reta s possui a mesma medida do raio: D = r. Lembre-se que o segmento que liga o centro à reta forma um ângulo reto no encontro!

• Reta secante à circunferência: é aquela que possui 2 pontos de intersecção. Assim, a distância do centro da circunferência até o ponto mais próximo da reta é menor que o raio da circunferência: D < r.

Posições relativas entre duas circunferências

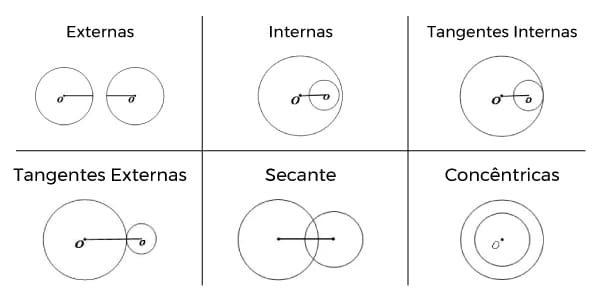
Por fim, podemos dizer que, ao comparar duas circunferências, também há nomes próprios para as posições que elas assumem!

• Não possuem pontos em comum

Quando elas não possuem pontos em comum, podem estar dispostas uma dentro da outra ou completamente do lado de fora. (Observe a imagem acima)

No primeiro caso, dizemos que são internas e a distância entre elas é dada por D < r1 – r2.

No segundo caso, dizemos que são externas e a relação é dada por D > r1 + r2.

• Possuem 1 ponto em comum (Tangentes)

Quando elas possuem 1 ponto de intersecção, também podem estar dispostas uma dentro da outra ou do lado de fora. (Observe a imagem acima)

No primeiro caso, dizemos que são tangentes internas e a distância entre elas é dada por D = r1 – r2.

No segundo caso, dizemos que são tangentes externas e a relação é dada por D = r1 + r2.

• Possuem 2 pontos em comum (Secantes)

Quando elas possuem 2 pontos de intersecção, só podem estar dispostas de uma forma. (Observe a imagem acima)

A relação de serem secantes é representada por r1 – r2 < D < r1 + r2.

• O que são Circunferências concêntricas?

Chamamos de circunferências concêntricas aquelas que têm o centro ocupando o mesmo ponto, independente do tamanho de seus raios. Nesse caso, a distância entre os centos é nula: D = 0.

Gostou do nosso artigo sobre Geometria Analítica? Confira outros artigos do nosso blog e se prepare para o Enem da melhor maneira! Você também pode se organizar com o nosso plano de estudos, o mais completo da internet.